В статье представлена история возникновения метаматериалов, обобщены принципы их работы. Рассмотрены способы создания метаматериалов при помощи массивов резонаторных ячеек. Показаны существующие разновидности SRR-колец.
Ключевые слова:метаматериал, DNG-материал, SRR-кольца.
Теоритические основы работы DNG-метаматериалов.
Важнейшими параметрами, характеризующими электродинамические свойства материалов, являются диэлектрическая ε и магнитная µ проницаемости. В зависимости от знака этих проницаемостей, гипотетически могут существовать 4 типа материалов: DNG (Double Negative), DPS (Double Positive), MNG (µ Negative) и ENG (ε Negative). Рассматриваемые DNG-материалы не существуют в природе, следовательно, могут быть получены лишь искусственно [2]. При этом наиболее распространены в природе DPS-материалы. Достичь DNG свойств позволяют метаматериалы, представляющие собой искусственные структуры, электромагнитные свойства которых выходят за рамки обычных представлений. При этом размер структурной единицы метаматериала должен быть существенно меньше длины волны излучения, благодаря чему волна будет воспринимать материал как однородный, обладающий некоторыми эффективными значениями диэлектрической и магнитной проницаемостей, не отличая его от обычных природных материалов. Сам термин метаматериалы был предложен руководителем Центра электромагнитных материалов и устройств в Остине (штат Техас, США) Роджером Уолсером в 2000г.
Впервые существование материалов в одновременной отрицательностью диэлектрической и магнитной проницаемостей предположил советский физик Виктор Веселаго в 1967г в работе [1]. 32 года работа Веселаго оставалась без должного внимания в силу отсутствия соответствующего материала. Однако, в 1999г. английский физик Джон Брайан Пендри с коллегами опубликовали статью [3], посвященную физике отрицательных диэлектрической и магнитной проницаемостей, где также предложили возможные конструкции метаматериалов, обладающими левыми свойствами (LHM — Left-handed metaterial), в частности, в этой статье впервые были предложены SRR-кольца (Split Ring Resonator), обладающие отрицательной µ (см. рис. 1).

Рис. 1. Массив SRR-колец Пендри [3]
Примерно через год после этого Дэвид Смит с соавторами в статье [4] предложили DNG-метаматериал, в котором были использованы придуманные Пендри SRR-кольца для получения отрицательной магнитной проницаемости и отрезки прямых проводников для получения отрицательной диэлектрической проницаемости. Эффект отрицательного преломления в этой статье был зафиксирован в диапазоне от 4,8 до 5,1 Ггц. Вскоре после этого LHM-материалы и отрицательное преломление (достигается при одновременной отрицательности Ɛ и µ) были продемонстрированы экспериментально.
Особенность LHM-метаматериалов состоит в том, что векторы H, E и k (определяющий направление групповой скорости волны) в них образуют не правую, а левую тройку векторов. При этом вектор Пойнтинга, определяющий направление распространения энергии ЭМВ и направление ее групповой скорости, по-прежнему образует с векторами Е и Н правую тройку. Следовательно, групповая и фазовая скорости в LHM-метаматериале направлены противоположно.
Однако, величина волнового сопротивления среды не может быть отрицательна, и у DNG-метаматериала она положительна. Как известно, волновое сопротивление среды определяется по формуле:
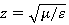 (1)
(1)
Отсюда легко понять, что если ЭМВ падает на границу раздела двух сред, одна из которых имеет положительные значения Ɛ и µ, а вторая — DNG-метаматериал со значениями Ɛ и µ, равными по модулю и противоположными по знаку значениям проницаемостей для первой среды, то ЭМВ не претерпевает отражения от границы раздела, так как волновые сопротивления сред оказываются одинаковы. Таким образом, преломленная волна распространяется во второй среде по той же стороне от нормали к границе раздела, что и падающая.
Рассмотренные в вышеупомянутой статье [4] кольца демонстрировали положительную µ на частотах ниже резонансной, и, совершенно неожиданно, отрицательную µ на частотах, совсем немного больших резонансной (см. рис. 2).
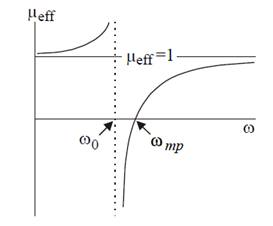
Рис. 2. Зависимость µэфф от частоты для массива SRR-колец [3, с.8]
На рис. 2, ω0 — резонансная частота, а ωmp — магнитная плазменная частота, на которой эффективная магнитная проницаемость среды обращается в нуль, по аналогии с тем, как диэлектрическая проницаемость плазмы обращается в нуль на плазменной частоте. Как видно на графике, именно в интервале между ω0 и ωтр эффективная магнитная проницаемость принимает отрицательные значения. Оба параметра определяются геометрией метаматериала, например, для SRR-колец они определяются по следующим формулам:
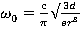 , (2)
, (2)
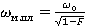 , (3)
, (3)
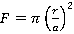 , (4)
, (4)
где d — ширина промежутка между соосными кольцами, а — период решетки SRR-колец, r — радиус внутреннего кольца.
А µэфф определяется по формуле:
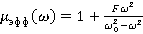 (5)
(5)
Эквивалентная схема SRR-колец показана на рис. 3.
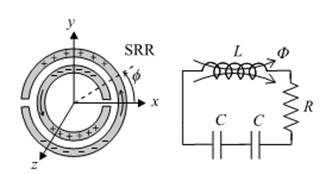
Рис. 3. Эквивалентная схема SRR [6]
Необходимо отметить, что LC-резонансы идеально проводящих металлов (например, SRR-колец) представляют собой геометрические LC-резонансы (GLC-резонансы). Частоты LC-резонансов определяются геометрией разомкнутого кольца и его размерами, а не электромагнитными свойствами металла. На эту модель можно полагаться лишь в том диапазоне частот, в котором метал можно считать проводником. Традиционно такие структуры предлагались для СВЧ, затем подобный метод получения отрицательной µ был распространен на средний ИК диапазон [7,8]. Но при переходе в оптический диапазон спектра, ввиду того, что размеры наноструктур становятся меньше глубины скин-слоя, электромагнитный отклик в металлах имеет плазменную природу, и ключевую роль в электродинамический свойствах метаматериала играет не GLC, а плазмонные резонансы — электрический поверхностный плазмонный резонанс (ППР) и магнитный плазмонный резонанс (МПР). Необходимо помнить, что с ростом частоты растут и потери.
Необычность электродинамических свойств SRR-колец заключается также в том, что обычные, природные материалы на гигагерцевых и выше частотах не проявляют магнитных свойств, для них µ=1. Исключение здесь составляют ферриты, магнетизм которых исчезает на частотах выше 10 Ггц. И только метаматериалы обладают магнитными свойствами на частотах гораздо выше 10 Ггц, охватывая ИК и даже оптический диапазон, в зависимости от свойств металла и геометрии структур.
Достичь отрицательности эффективной диэлектрической проницаемости среды позволяет композитный материал, составленный из прямых отрезков проводников (см. рис. 4).
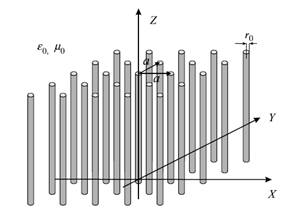
Рис. 4. Массив проводников обеспечивающий отрицательность εэфф [6]
Для отрезков прямых проводников GLC-резонансы определяются толщиной провода, которая намного больше глубины скин слоя. А при переходе в оптическую область частот, при возникновении уже плазмонных резонансов, фактор усиления зависит только от диэлектрической проницаемости металла и отношения линейных размеров проводника. На рис. 5 показана аналогия между плазмонным резонансном в металлической наночастице и резонансном в RLC-контуре [4].
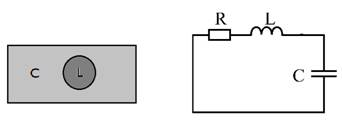
Рис. 5. Аналогия между плазмонным резонансом и резонансом RLC-контура [4, с. 18]
При Ɛ(ω)>0, в диапазоне частот ω0< ω< ωпл дисперсионная зависимость для метаматериала будет иметь запрещенную зону (стоп-зону), или диапазон запрещенных частот, в котором метаматериал будет работать как полосозаграждающий фильтр. А с введением в структуру массива отрезков прямых проводников, обладающих отрицательной Ɛ (то есть при превращении материала с отрицательной µ в DNG-ММ), ММ начинает вести себя уже как полосопропускающий фильтр в том же диапазоне частот [6]. Геометрия такого DNG метаматериала приведена на рис. 6. Чтобы избежать влияния отрезков прямых проводников на магнитные свойства SRR-колец, необходимо вынести отрезки из областей концентрации магнитного поля в кольцах.

Рис. 6. Экспериментальный образец DNG-метаматериала
Для резонансного возбуждения прямых отрезков проводников необходимо, чтобы длина волны излучения была кратна половине длины отрезков:
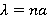 , (6)
, (6)
где а — половина длины стержня. Чаще всего рассматривают диапазон длин волн λ>2a, который включает наиболее важный полуволновой резонанс при 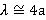 .
.
Низкочастотная диэлектрическая проницаемость не зависит от частоты, однако на высоких частотах становится дисперсионной. Необходимо максимально приблизить диапазон отрицательности диэлектрической проницаемости, заключенному между электронной резонансной частотой и электронной плазменной частотой. Эффективная плазменная частота электронов в прямом отрезке металлической проволоки:
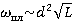 , (7)
, (7)
где L — коэффициент самоиндукции на единицу длины, d — длина отрезка проводника.
Поскольку диэлектрическая и магнитная проницаемость — комплексные величины, требуется преобладание в них действительных частей — большая величина мнимых частей не позволяет наблюдать отрицательное преломление. Минимизировать потери в метаматериале можно, например, охлаждая ММ до сверхнизких температур. Наиболее подробно электродинамика метаматериалов описана в книгах [4] и [5].
Обзор публикаций.
Остановимся более подробно на примерах практической реализации метаматериалов. Существует множество вариаций традиционной конструкции кольцевых резонаторов. В зависимости от того, какую необходимо получить резонансную частоту ω0 (для излучения в СВЧ диапазоне), варьируются такие параметры как: диаметр колец, расстояние между внешним и внутренним кольцом, количество и величина разрезов колец и т. д. Примеры использования различных исполнений кольцевых резонаторов можно найти в статьях [9–14].
Напомним, что массив SRR колец обеспечивает только отрицательную магнитную проницаемость µ и для того, чтобы реализовать DNG-среду понадобится дополнить ее массивом из электрических резонаторов. Чтобы избежать такого усложнения конструкции, в статьях [15–17] предлагается создать массив из включений в форме «S» (см. рис 7а), который характеризуется одновременной отрицательностью ε и µ. Проведено моделирование, представлены полученные результаты подтверждающие левый характер полученной среды.
Другой отрицательной особенностью использования массивов традиционных SRR является бианизотропность (одновременное присутствие диэлектрической и магнитной анизотропии) полученных сред. В статьях [18,19] описывается это явление и предлагается улучшенная конструкция SRR-колец — BC-SRR (Broadside-Coupled SRR). Основное ее отличие от SRR, предложенных Пендри, состоит в том, что вместо внутреннего кольца используется другое, по обратную сторону подложки (см. рис 7б).
Такая модификация позволила избавиться от бианизотропности среды и, как следствие, нежелательных кросс поляризационных эффектов.
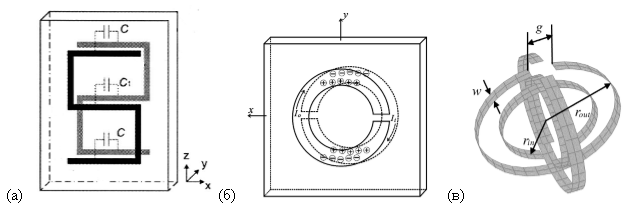
Рис. 7. Модифицированные SRR. S-образная конструкция [15] (а); конструкция BC-SRR и распределение в нем зарядов [18] (б); двумерная конструкция CSRR [21]
Еще одна модификация колец, предложена в статьях [20,21]. В них метаматериал формируется при помощи двумерных пресекающихся двойных колец — CSRR (Crossed-SRR). Конструкция колец изображена на рис. 7в. Явным преимуществом рассмотренной конструкции является то, что среда, полученная из трехмерного массива таких колец, обладает изотропностью под любым углом распространения излучения.
Отдельного внимания заслуживают особенности использования метаматериалов для работы с излучением имеющим круговую поляризацию. В статье [22] описан один из способов создания такой среды. Вместо традиционных SRR — колец в ней применен массив из замкнутых рамок с диагональной полосой внутри (рис. 8а). Использование метаматериала позволило улучшить импеданс и коэффициент усиления антенны.
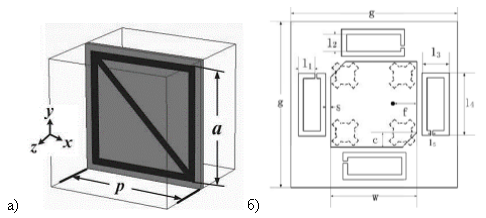
Рис. 8. Варианты конструкции колец для излучения с круговой поляризацией. Резонатор в виде квадратной рамки(а); прямоугольные SRR, расположенные вокруг печатной антенны [23] (б)
Еще один пример использования метаматериала для поляризованного излучения описан в статье [23]. В ней используются 4 квадратных кольца с разрезами, расположенные вокруг печатной антенны. С их помощью удалось увеличить ширину рабочего диапазона частот антенны без увеличения габаритов. Способ расположения колец представлен на рис. 8б.
Заключение.
В заключение хотелось бы отметить, что в данной обзорной статье представлены только самые базовые сведения о технологии метаматериалов. Их популярность увеличивается с каждым днем и растущее число научных статей на эту тему доказывает это. К числу уже открытых применений ММ можно отнести создание частотно-селективных поверхностей, всевозможные улучшения свойств антенн, линзы со сверхразрешением и многое другое. Перспективность данного направления трудно переоценить и в ближайшее время вероятно будут обнаружены новые полезные применения метаматериалов.
Литература:
1. В. Г. Веселаго, Электродинамика веществ с одновременными отрицательными значениями Ɛ и µ, Успехи Физических Наук, т. 92, вып. 3, с. 517–525, 1967.
2. Allison Denise Kipple, Fundamental Investigations of Double-Negative (DNG) Metamaterials Including Applications for Antenna Systems — Volume 65. Issue 12. — P. 6555.; 262 p.
3. J. B. Pendry [et al]. “Magnetism from Conductors and Enhanced Nonlinear Phenomena.” IEEE Transactions on Microwave Theory and Techniques 1999 — Volume 47. Issue 11. — P. 2075–2084.
4. Электродинамика метаматериалов / Пер. С англ. В. Г. Аракчеева, Ю. В. Владимировой — М.: Научный мир, 2011–224 с.
5. Электромагнитные процессы в среде, наноплазмоника и метаматериалы: Учебное пособие / В. А. Астапенко — Долгопрудный: Издательский дом «Интеллект», 2012. — 584 с.
6. Metamaterials with negative parameters: theory, design and microwave applications / Ricardo Marque´ s, Ferran Martin, Mario Sorolla — Wiley, 2008. — 315p.
7. S. Linde, C. Enkrich, M. Wegener, J. Zhou, T. Koschny, and C. M. Soukoulis. Science, 306:1351,2004.
8. N. Katsarakis, T. Koschny, M. Kafesaki, E. N. Economy, and C. M. Soukoulis. Appl. Phys. Lett., 84:2943, 2004.
9. Composites with tuned effective magnetic permeability, Alireza V. Amirkhizi and Sia Nemat-Nasser, J. of App. Phys. 102, 014901, 2007.
10. Composite Medium with Simultaneously Negative Permeability and Permittivity, D. R. Smith, Willie J. Padilla, D. C. Vier, S. C. Nemat-Nasser, S. Schultz, Phys. Rev. Lett. 84, [4184] (1999).
11. Experimental observation of left-handed transmission in a bilayer metamaterial under normal-to-plane propagation, Kaan Guven, M. Deniz Caliskan, and Ekmel Ozbay, Opt. Express 14, 8685–8693, 2006.
12. Optical bandpass filter using split ring resonators, A. Zarifkar, A. Rahmani, Progress In Electromagnetics Research M, Vol. 2, 93–103, 2008.
13. Enhanced transmission of electromagnetic waves through split-ring resonator-shaped apertures, Levent Sahin, Koray Aydin, Gonul Turhan Sayan, Ekmel Ozbaya, Journal of Nanophotonics, 5(1) [051812], 2011.
14. Transmission Properties Of Stacked Srr Metasurfaces In Free Space, M. Aznabet [et.al], Progress In Electromagnetics Research M, Vol. 20, 1–11, 2011.
15. Design and Simulation of Double “S” Shaped Metamaterial. Hayet Benosman, Nouredine Boukli Hacene, JCSI International Journal of Computer Science Issues, Vol. 9, Issue 2, No 1, March 2012.
16. Magnetic Properties Of S-Shaped Split-Ring Resonators, H. S. Chen, L. X. Ran, Progress In Electromagnetics Research, PIER 51, 231–247, 2005.
17. Left-handed materials composed of only S-shaped resonators. Hongsheng Chen, Lixin Ran, Physical review E 70, 057605, 2004.
18. [18] R. Marque´ s, F. Medinaand R. Rafii-El-Idrissi “Role of bi-anisotropy in negative permeability and left handed metamaterials.” Phys. Rev. B, vol. 65, paper 144441, 2002.
19. [19] R. Marque´ s, F. Mesa, J. Martel, and F. Medina “Comparative analysis of edge and broad-side coupled split ring resonators for metamaterial design. Theory and experiment.” IEEE Trans. Antennas Propag., vol. 51, pp. 2572–2581, 2003.
20. [20] Performance Analysis of Metamaterials With Two-dimensional Isotropy, Hai-Ying Yao, Le-Wei Li, High Performance Computation for Engineered Systems, 2004.
21. [21] Macroscopic Performance Analysis Of Metamaterials Synthesized From Microscopic 2-D Isotropic Cross Split-Ringresonator Array, H.-Y. Yao, Progress In Electromagnetics Research, PIER 51, 197–217, 2005.
22. [22] Simultaneous gain and bandwidths enhancement of a single-feed circularly polarized microstrip patch antenna using a metamaterial reflective surface, S. Chaimool, K. L. Chung, and P. Akkaraekthalin, Progress In Electromagnetics Research B, Vol. 22, 23–37, 2010.
23. [23] A new method for broadening bandwidths of circular polarized microstrip antennas by using DGS & parasitic split-ring resonators, Z.-B. Deng, W. Jiang, S.-X. Gong, Y.-X. Xu, and Y. Zhang, Progress In Electromagnetics Research, Vol. 136, 739–751, 2013.







