В статье предлагается разработка методики формирования портфелей ценных бумаг с применением спектральных асимметричных мер риска.
Инвесторы — лица, которые владеют определенным количеством акций разного срока действия и разной ценности. Главной задачей для них является правильное управление и вложение этих акций, а главной целью — получение наибольшей прибыли и минимизация рисков. При этом им необходимо сформировать портфели акций, которые отвечают их требованиям, то есть оптимальные портфели. Именно потому, что инвесторы по-разному могут относиться к прибылям и убыткам, в этой работе была учтена асимметрия этого отношения. Были введены показатели, которые показывают, насколько инвестор положительно относится к риску, даже если этот риск сулит ему определенные потери и показатель, характеризующий неприятие риска, даже если в будущем будут довольно большие прибыли. В работе рассматривается задача формирования портфеля ценных бумаг с применением к нему в дальнейшем спектральных асимметричных мер риска. Эта задача довольно традиционна и уже известны некоторые подходы к её решению. Особенностью же данной работы является предложенный асимметричный вариант спектральных мер риска, учитывающий различные отношения инвестора к прибылям и убыткам.
Появление мер риска явилось естественной попыткой оценить одним числом возможные потери портфеля финансовых инструментов при колебаниях рынка. Они также дают возможность оценить размер капитала, который необходимо резервировать для покрытия этих потерь.
Мера риска необходима, прежде всего, для:
1) Определения рискового капитала, т. е. определения капитала необходимого финансовому учреждению для покрытия неожиданных убытков.
2) Как инструмент управления — это означает, что меры риска используются менеджментом для того, чтобы оценивать и контролировать уровень риска, принятый подразделением компаний. [1]
Большинство рисков вне зависимости от их физической природы имеет финансовые последствия.
Спектральная мера риска является функцией доходности портфеля и показывает количество нумератора (обычно валюты), которая должна быть в запасе. Преимущество спектральных мер риска заключается в том, каким образом они могут быть связаны с неприятием риска, и, в частности с функцией полезности, где через веса указывается возможная прибыль портфеля. [2]
Спектральная мера риска Mϕ может быть определенна по следующей формуле:
Mϕ(X)=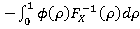 (1)
(1)
Где Мф(Х)- мера риска для портфеля Х,
Fх-1(р)-это обратная функция распределения для Х. [3]
В этой работе вводится понятие асимметричной меры риска, потому, что различные инвесторы по-разному могут относиться к рискам и потерям.
Если есть функция распределения доходности, где p* это её значение в 0, положительная часть функции и отрицательная часть такие, как это показано на Рис.1.
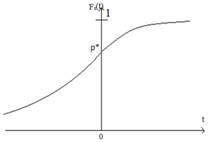
Рис.1.
Формула для определения асимметричной спектральной меры риска выглядит как:
Mϕ=-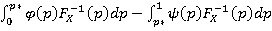 (2)
(2)
Предположим, что φ(р)=pα, ψ(р)=pβ. α и β здесь — показатели отношения инвестора к положительным и отрицательным рискам. То есть при отрицательных значениях функции распределения используется параметр β, а при положительном значении используется параметр α. Таким образом, формулу (2) можно представить как:
Mϕ=-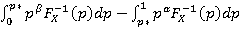 (3)
(3)
Где Мф(Х)- мера риска для портфеля Х,
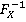 -это обратная функция распределения для Х,
-это обратная функция распределения для Х,
ϕ(р)- неотрицательная, не возрастающая, непрерывная интегрируемая функция, определенная на [0;1].
α и β — степень, в которую возводится показатель 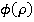 , зависящая от отношения инвестора к положительным и отрицательным рискам. То есть при ρ≤0 используется коэффициент β, а при ρ>0 используется α.
, зависящая от отношения инвестора к положительным и отрицательным рискам. То есть при ρ≤0 используется коэффициент β, а при ρ>0 используется α.
ρ — доходность портфеля, которая может быть вычислена по формуле:
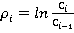 (4)
(4)
Где Ci- цена акции в момент времени i,
Ci-1-цена акции в момент времени i-1.
Статистическая оценка спектральных асимметричных мер риска:
Мф(Х)=-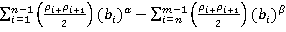 (5)
(5)
Таким образом, в дальнейших расчетах будет использоваться формула (5) учитывающая асимметрию распределения случайной величины. Необходимость учета асимметрии заключается в различном отношении инвесторов к рискам.
Алгоритм решения задачи.
Перейдем непосредственно к рассмотрению программы, которая была создана мной в среде Microsoft Visual Studio 2010 и производит все вычисления и необходимые расчеты.
1) В качестве исходных данных взяты ежедневные цены акций пяти компаний за годовой период. Я использовала цены акций пяти компаний таких как “Газпром”, “Лукойл”, “Автоваз ”, “Роснефть”, “Сбербанк”. Данные были взяты с официального сайта http://www.finam.ru/. Также, в начале, стоит задать коэффициенты α и β. Эти коэффициенты задаются инвестором в зависимости от его отношения к риску. В данной работе было принято, что они принадлежат интервалу от 0 до 2. Если инвестор решает, что не склонен к риску, даже если получит при этом небольшую прибыль, то β>α, если же он готов рисковать, пусть даже это грозит потерей какой-то суммы, но при этом получить максимальный доход, то он задает α>β.
2) Запускаем программу, созданную для вычисления мер рисков, а также графического отображения полученных результатов в среде Microsoft Visual Studio 2010.
3) Заносим исходные данные в программу. Для этого нажимаем “Открыть файл с исходными данными” и выбираем файл, в котором находятся данные по ценам пяти акций за годовой период. Нормирование данных выполняется программой автоматически.
Для нормирования данных по первой акции используется следующая формула:
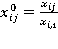 (6)
(6)
где 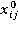 –нормированная цена i-ой акции в момент времени j,
–нормированная цена i-ой акции в момент времени j,
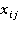 — цена i-ой акции в момент времени j,
— цена i-ой акции в момент времени j,
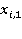 — цена i-ой акции в первый момент времени момент времени.
— цена i-ой акции в первый момент времени момент времени.
Операция нормирования необходима для приведения данных к сопоставимому виду.
Также здесь инвестор задает α и β. Как видно на рисунке 3 они задаются окошках внизу.
4) Следует выбрать доли акций каждой компании в формируемом портфеле. Программа сама их выбирает случайно, подчиняясь правилу, что первые четыре доли — a1,a2,a3,a4 выбираются случайно и лежат в промежутке от 0 до 1, при этом 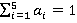 . Если будет выполняться условие, что
. Если будет выполняться условие, что 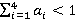 , пятая доля — x5 будет соответственно определена по формуле:
, пятая доля — x5 будет соответственно определена по формуле:
a5=1-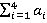 (7)
(7)
Если же сумма окажется не меньше и не равной единице, то значения a1,a2,a3,a4 не используются, и программа дальше продолжает подбирать подходящие значения. Значения сгенерированных ai будут отображены во вкладкеa(i).
Также, чтобы получить достаточное для анализа количество точек, следует задать количество рядов со сгенерированными долями, это значение можно ввести в окошке “Количество рядов случайных чисел”.
5) Находятся цены портфелей акций. Используемая для этого формула:
Пi= a1*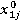 +a2*
+a2*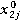 +a3*
+a3*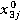 +a4*
+a4*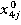 +a5*
+a5*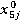 (8)
(8)
где a1,a2,a3,a4,a5 это ранее сгенерированные доли каждой акции в портфеле,
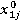 ,
, 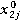 ,
, 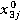 ,
, 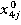 ,
, 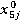 - это цены акций компаний в момент времени j.
- это цены акций компаний в момент времени j.
Значения цен портфелей можно посмотреть во вкладке “Графики”→“П(i)”.
6) Следующей операцией программы будет нахождение доходности портфеля- 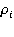 , по ранее представленной формуле (4). Доходность портфеля в последующем понадобится для вычисления конечного значения асимметричной меры риска по формуле (5). Эти значения можно посмотреть во вкладке “ρ(i)”.
, по ранее представленной формуле (4). Доходность портфеля в последующем понадобится для вычисления конечного значения асимметричной меры риска по формуле (5). Эти значения можно посмотреть во вкладке “ρ(i)”.
7) Строим нормированную гистограмму доходностей портфелей акций. Для этого находим максимальное и минимальное значения доходностей портфелей — ρ1<ρ2<ρn< ρ* < ρn+1 <….<ρm-значения доходностей в порядке возрастания, ρ1- min значение доходности портфеля, ρm-max значение доходности портфеля, и полученный отрезок разбиваем на равные части, их количество зависит от того, сколько точек попадает в каждую часть. В данной работе было принято, что в каждой части должно находится примерно по 15–20 значений, далее количество попавших в интервал точек делим на общее число точек, для того, чтобы вычислить высоту столбцов гистограммы. Используется формула:
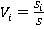 (9)
(9)
Где Siколичество точек, попавших в интервал
— S- общее число точек.
В программе гистограмма выглядит следующим образом:
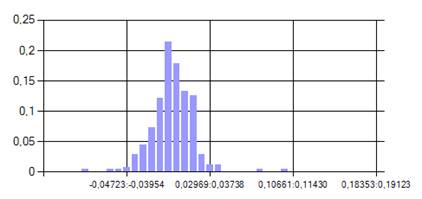
Рис. 2. Гистограмму доходностей портфелей
Данные по количеству точек можно посмотреть во вкладке “расчеты”.
Изменить количество интервалов можно в окошке “Количество интервалов”.
8) Строим эмпирическую функцию распределения. Здесь используется предыдущая гистограмма, а точнее высоты столбцов. Для Создания гистограммы эмпирической функции распределения необходимо складывать высоты столбцов нормированной гистограммы доходностей портфелей, таким образом, что:
b1=v1, b2=v1+v2,…, bi=v1+v2+…+vi,
Где bi-значение i-го столбца гистограммы эмпирической функции распределения, а vi- значение i-го столбца нормированной гистограммы доходностей портфеля.
Данные этой гистограммы в дальнейшем нам понадобятся для вычислений мер риска.
Полученная гистограмма:
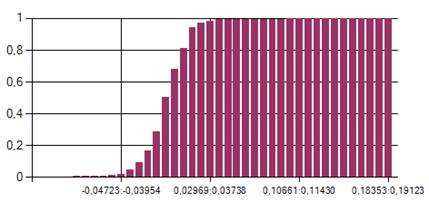
Рис. 3 Эмпирическая функция распределения
9) Программа переходит непосредственно к вычислению мер риска. Для реализации формулы (5) были заданы коэффициенты α и β. Рядом с окошком, в котором задаются эти показатели, есть кнопка “Расчет”, после её нажатия на программа сама подсчитывает меру риска для портфеля по представленной ранее формуле, причем если значения эмпирической функции распределения отрицательные, выбирается параметр β, если положительные, то α.
10) Далее меры риска, а также доходности всех портфелей наносятся на график. Доходности портфелей вычисляются по формуле
|
(10) |
Di=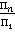 (10)
(10)
где Пn-цена портфеля в конечный момент времени,
П1- цена портфеля в начальный момент времени.
Конечный график можно увидеть во вкладке “Конечный график”.
При построении конечного графика выделяется эффективная граница портфелей оптимальных по Парето.
Эта граница состоит из портфелей, которые не улучшаются, т. е. доходность не увеличивается и риск не уменьшается. Из этих портфелей инвестор, полагаясь на свою функцию полезности, может выбрать оптимальный для себя портфель. В этой работе не будет дано рекомендаций по выбору портфелей для инвесторов, так как работа носит исследовательский характер. Получаем конечный график при α=1,β=0.
Изменяя α и β (отношение инвестора к рискам) можно проследить за изменением эффективной границы Паретто.
По полученным графикам можно будет определить, при каком изменении параметров происходит изменение доходностей и рисков. Можно также оценить количество оптимальных портфелей, попавших в границу Парето. Их можно посмотреть во вкладке “Граница Парето”.
Таким образом, в моей работе были введены в рассмотрение асимметричные спектральные меры риска, которые отражают различные отношения инвесторов к доходам и потерям. Асимметричные спектральные меры риска были применены к анализу портфелей ценных бумаг, а также был разработан программный продукт, который по данным позволяет строить эффективное множество портфелей.
Литература:







