Теоретически рассмотрены условия и характер спонтанного ориентационного фазового перехода, и ориентационного фазового перехода, индуцированного в кубическом магнетике механическими напряжениями.
Ключевые слова: редкоземельные ферриты-гранаты, термодинамическая теория,фазовые переходы, кубический магнетик.
Известно, что доменная структура редкоземельных феррит — гранатов (РЗФГ) в области магнитных ориентационных фазовых переходов становится неустойчивой, а подвижность доменных границ существенно изменяется [1]. Следовательно, вблизи фазовых переходов влияние внешних воздействий (электрического и магнитного полей, давления и т. д.) на доменную структуру становится наиболее существенным, что позволяет управлять доменной конфигурацией материала относительно слабыми полями, получение которых не связано с техническими трудностями. Если к тому же иметь в виду известный термомагнитный способ записи/стирания информации при переходе температуры магнитной среды через точку компенсации или температуру спиновой переориентации [2], то можно заключить, что исследования параметров и свойств доменной структуры РЗФГ в области магнитных фазовых переходов являются приоритетными для области современного материаловедения, занимающейся поиском и созданием материалов для элементной базы приборов спиновой электроники нового поколения, принцип работы которых основан на изменении доменной конфигурации материал под действием электрического и магнитного полей.
В то же время, как показали последние экспериментальные исследования, существующая теория часто не может адекватно описать наблюдаемое изменение доменной структуры РЗФГ в области ориентационных фазовых переходов; более того, иногда выводы существующей теории противоречат данным эксперимента. Поэтому исследования закономерностей динамики перестройки доменной структуры, а также связанных с этим изменений актуальных для практических приложений физических свойств (магнитной восприимчивости, коэрцитивной силы и т. п.) ферритов-гранатов в области магнитных ориентационных фазовых переходов представляют не только прикладной, материаловедческий, но и значительный академический интерес, расширяя и дополняя существующие представления физики магнитных доменов.
РЗФГ — многоосные ферримагнетики, обладающие сложной магнитной структурой, формирующейся обменно связанными между собой ионами железа и ионами железа и редкоземельными ионами. Это определяет достаточно сложное для теоретического описания поведение многих физических свойств этих ферримагнетиков, в частности, немонотонную температурную зависимость спонтанной намагниченности и наличие температуры магнитной компенсации в ферритах-гранатах с тяжелыми редкоземельными ионами.
В нулевом магнитном поле энергия однодоменного кристалла определяется лишь его энергией магнитной анизотропии. Ограничиваясь двумя членами разложения энергии магнитной анизотропии кубического кристалла в ряд по направляющим косинусам в сферических координатах с полярной осью [001], получим [3]
Е = Еа = [К1 sin22θ + (K1 + K2 cos2θ)sin4θcos22φ], (1)
где K1 и K2 — первая и вторая константы кубической анизотропии, θ — полярный угол спонтанного магнитного момента (угол между вектором Ms и полярной осью), φ — азимутальный угол спонтанного магнитного момента (угол между вектором Ms и осью [010]).
Из минимизации (1) по θ и φ, следует, что при всех возможных соотношениях между K1 и K2 системе уравнений
∂Е/∂θ = 0, ∂Е/∂φ = 0,
∂2Е/∂θ2 > 0, ∂2Е/∂θ2∂2Е/∂φ2 — (∂2Е/∂θ∂φ)2 > 0,
удовлетворяют только ориентации вектора Ms вдоль трех различных кристаллографических направлений: типа [100] (ребро куба), типа [110] (диагональ грани) и типа [111] (диагональ куба).
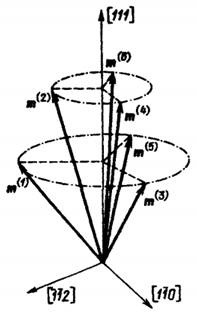
Рис. Зонтичная структура магнитных моментов редкоземельных ионов в ферритах-гранатах.
Для каждого из этих направлений минимум энергии кристалла реализуется при определенных соотношениях между константами анизотропии K1 и K2 [2]:
- ориентация вектора Ms вдоль оси [100] при K1 ≥ 0; (2 а)
- ориентация вектора Ms вдоль оси [110] при 0 ≥ K1 ≥ — K2/2; (2 б)
- ориентация вектора Ms вдоль оси [111] при K1 ≤ — K2/3. (2 в)
Наряду с устойчивыми направлениями вектора спонтанного магнитного момента в кубическом кристалле существуют седловые точки, лежащие в кристаллографической плоскости типа (110), в которых ориентация вектора Ms метастабильна. Для них выполняется соотношение [2]:
sin2θ = — 2K1/ K2.
Равенства в соотношениях (2) соответствуют линиям потери устойчивости фазы с определенной ориентацией вектора Ms, и как видно из этих соотношений, имеются области значений констант K1 и K2, при которых различные магнитные фазы сосуществуют.
Подставляя соотношения (2) в (1), находим, что
- переход между фазами [100] и [110] происходит при условии
K1 = 0, K2 ≥ 0; (3 а)
- переход между фазами [110] и [111] происходит при условии
9K1 + 4K2 = 0, K1 ≤ 0; (4 б)
- переход между фазами [111] и [100] происходит при условии
9K1 + K2 = 0, K1 ≥ 0. (5 в)
Таким образом, при учете только первой и второй констант магнитной кубической анизотропии осями легкого намагничивания в кубическом магнетике могут быть только оси типа [100], [110] и [111]. Следовательно, в рамках данного приближения ориентационные переходы одной магнитной фазы в другую в кубических магнетиках при Н = 0 всегда происходят скачком, то есть всегда являются фазовыми переходами I — ого рода.
Отметим, что в области существования той или иной магнитной фазы при изменении констант кубической анизотропии могут меняться направления осей трудного намагничивания [2]:
в фазе [100] осью трудного намагничивания является
- ось [111] при 9K1 + 4K2 > 0,
- ось [110] при 9K1 + 4K2 < 0,
в фазе [110] осью трудного намагничивания является
- ось [111] при 9K1 + K2 > 0,
- ось [100] при 9K1 + 4K2 < 0,
в фазе [111] осью трудного намагничивания является
- ось [100] при K1 < 0,
- ось [110] при K1 > 0.
В заключение отметим следующие особенности рассмотренных фазовых переходов: при учете только первой и второй констант анизотропии легкими осями намагничивания в кубическом кристалле могут быть только оси типа [100], [110] и [111] и равновесных угловых фаз не возникает, следовательно, переходы из одной магнитной фазы в другую в кубическом магнетике в нулевом магнитном поле всегда происходят скачком (т. е. являются фазовыми переходами I-го рода).
Литература:
1. Parkin S. S. P. The magnetic racetrack memory: a shift register memory based on current induce precessional motion of domain walls. US Patent — 2006. — 7. — 031. — P. 178.
2. Белов К. П., Звездин А. К., Кадомцева А. М., Левитин Р. З. Ориентационные переходы в редкоземельных магнетиках. — М: Наука, — 1979. — 317 с.
3. Тикадзуми С. Физика ферромагнетизма. — М: Мир, — 1997. — 420 с.
4. Соколов Б. Ю., Шарипов М. З. Низкочастотный резонанс доменных границ в феррите-гранате Tb3Fe5O12 вблизи точки магнитной компенсации. // ЖЭТФ. — 2013. — Т.143. — В.5. — С. 895–899.







