Статья посвящена численному расчету долговечности такой механической системы как несущая конструкция главной балки металлургического мостового крана спектральным методом. В качестве выходных параметров системы рассматривается средний квадрат упругопластической деформации, возникающие при эксплуатации в мосте крана. По результатам расчетов построена кривая дифференциальной функции распределения, определена вероятность опасного состояния системы, что позволяет судить о ее долговечности.
Ключевые слова.Спектральный метод, вероятность опасного состояния, механическая система, надежность, долговечность, средний квадрат упругопластической деформации, несущая конструкция, металлургический кран, выходные и входные параметры системы, действующие нагрузки, напряжения.
Методика. Численный расчет расчета долговечности механической системы — несущей конструкции главной балки металлургического мостового крана грузоподъемностью 50 тонн осуществлены на основе теоретического обоснования спектрального метода.
Основная часть. Средняя величина упругопластической деформации характеризует рабочее состояние несущей конструкции главной балки металлургического мостового крана, сохранение ее функциональных свойств и определяется степенью накопленных повреждений и потери энергии в системе в процессе усталости.
Значительное деформирование элементов конструкции приводит к появлению и развитию необратимых процессов в поверхностных и внутренних слоях, снижению рабочих показателей системы. Поэтому, как уже указывалось раньше [1–14], величина упругопластической деформации представляет собой меру накопленных повреждений в механической системе, является показателем ее рабочего состояния, а значит и ее долговечности.
Обоснованным представляется подход к прогнозированию системы по долговечности на основе спектрального метода, но при этом необходимо учитывать вероятность достижения и пересечения выходным параметром допускаемого уровня, характеризующего предельный диапазон работы конструкции в упругой области.
Среднюю величину деформации определим, исходя из [5, 9, 10, 11], ε = 0,786 в относительных единицах. Тогда
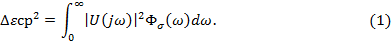
Где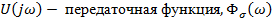 
— спектральная плотность распределения действующих нагрузок (напряжений изгиба) на механическую систему. Получим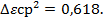 
Имея средний квадрат распределения упругопластической деформации, определим вид кривой её распределения. Определив значения плотности вероятности закона распределения для величины упругопластической деформации при известном значении дисперсии выходного процесса. Для нормального распределения ε и Dε подставим в формулу
построим кривую дифференциальной функции распределения рис. 1. На основании [5, 9, 10, 11, 13] Dε= 0,658.
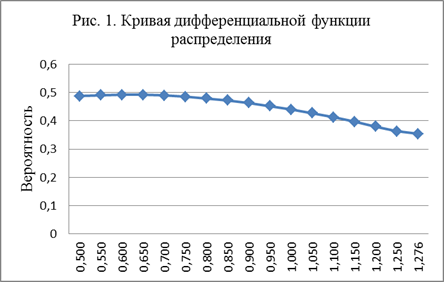
Определим вероятность опасного состояния механической системы — несущей конструкции главной балки металлургического мостового крана по нагруженности при известном уровне допускаемых значений упругопластической деформации от ε = 0,786 до εmax = 1,276. Это выполняется посредством вычисления величин интегральной функции закона для выбранных значений выходного параметра в координатах P-ε.
Для нормального закона распределения случайных величин процесса используем функцию Лапласа в виде
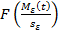— функция Лапласа.
Из [5, 9] имеем Mε(t) = 0,773, а sε= 0,811. Из таблиц находим 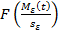= 0,3289.
Тогда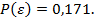 
Выводы. Полученная вероятность опасного состояния при имеющемся уровне упругопластической деформации характеризует появление различных по величине нагрузок на выходе сложной механической системы, что позволяет решить задачу о долговечности несущей конструкции главного балки моста металлургического крана.
Заключение. По результатам теоретического обоснования определения долговечности спектральным методом был проведен расчет и построена кривая дифференциальной функции распределения для выбранных значений выходного параметра. Определена вероятность опасного состояния механической системы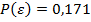 
, по которой можно судить о долговечности системы.
Литература:
1. Бархоткин В. В., Извеков Ю. А., Миникаев С. Р. Обзор аварий на крановом оборудовании металлургических производств. // Международный журнал прикладных и фундаментальных исследований. — Москва, РАЕ, 2013. — № 10–1. С. 9–11.
2. Бирюков М. П. Динамика и прогнозирующий расчет механических систем. // «Вышэйшая школа». — Минск, 1980. — 189 с: ил.
3. Извеков Ю. А. Анализ техногенной безопасности кранового хозяйства России. // Современные наукоемкие технологии. — Москва, РАЕ, 2012. — № 12. С. 18–19.
4. Извеков Ю. А., Кобелькова Е. В., Лосева Н. А. Анализ динамики и вопросы оптимизации металлургических мостовых кранов. // Фундаментальные исследования. — Москва, РАЕ, 2013. — № 6–2. С. 263–266.
5. Извеков Ю. А. Риск-анализ оборудования металлургических производств. Подход, концепция, анализ. Монография. — Saarbrucken, Deutschland. LAP Lambert, 2013. — 56 c.
6. Извеков Ю. А. Моделирование прогнозирования риска несущих конструкций кранов металлургического производства. // Актуальные проблемы современной науки, техники и образования. — Магнитогорск, МГТУ, 2012. № 70, Т. 1. С. 6–8.
7. Извеков Ю. А., Кобелькова Е. В., Лосева Н. А. Аналитическая оценка пластической деформации несущих конструкций металлургических мостовых кранов. — Магнитогорск, МГТУ, 2013. № 71, Т. 1. С. 48–51.
8. Извеков Ю. А. Математическое моделирование оценки упругопластической деформации несущих конструкций механических систем. // Современные тенденции в образовании и науке: сборник научных трудов по материалам Международной научно-практической конференции 31 октября 2013: в 26 частях. Часть 15; М-во обр. и науки. Тамбов: Изд-во ТРОО «Бизнес-Наука-Общество», 2013. С. 57–58.
9. Извеков Ю. А. Прогнозирование надежности несущих конструкций кранов металлургических производств. Вопросы. Гипотезы. Ответы: Наука XXI века: Коллективная монография. — Краснодар, 2013. Книга 6, часть 3, глава 9. С. 189–211.
10. Извеков Ю. А., Кузина Т. Г. Оценка упругопластической деформации на основе метода преобразования вероятностей. // Современные проблемы науки и образования. — 2013. — № 6; URL: www.science-education.ru/113–10810 (дата обращения 14.02.2014).
11. Izvekov Y. A., Dubrovsky V. V., Hamutskikh E. Y. Mathematical Modeling and Calculation of Accuracy and Durability of Mechanical Systems' Elements. // World Applied Sciences Journal 30 (1): pp. 32–34, 2014
12. Крылова Е. А., Извеков Ю. А. О подходе к оценке техногенной безопасности металлургического производства. // Успехи современного естествознания. Москва, РАЕ, 2012. — № 6. С. 32–33.
13. Извеков Ю. А. Вероятностный синтез сложной механической системы. // Молодой ученый. — 2014. — № 4. — С. 179–182.
14. Извеков Ю. А., Бирюков Д. А. Прогнозирование долговечности механических систем корреляционным методом. // Актуальные проблемы гуманитарных и естественных наук. — 2014. — № 3.
