Статья посвящена теоретическому обоснованию расчета долговечности такой механической системы как несущая конструкция главной балки металлургического мостового крана спектральным методом. В качестве входных параметров системы исследуются максимальные напряжения, возникающие в сечении несущей конструкции моста, а в качестве выходных — остаточная деформация и прогибы, возникающие при эксплуатации в мосте крана. Используется известный математический аппарат спектральной плотности случайного процесса с представленными формулами энергетического спектра между входными и выходными параметрами. Материал статьи позволит принимать верные решения при определении надежности и долговечности несущих конструкций металлургических мостовых кранов.
Ключевые слова: спектральный метод, спектральная плотность, энергетический спектр, механическая система, надежность, долговечность, упругопластическая деформация, несущая конструкция, металлургический кран, выходные и входные параметры системы, действующие нагрузки, напряжения.
Введение. Основой спектрального метода является одноимённая плотность, которая представляет собой мощность процесса на единицу полосы частот. Понятие спектральной плотности можно применить и к задачам, для которых трудно в обычном физическом смысле определить мощность по частотам [2], например, спектральная плотность распределения упругопластической деформации в механической системе — несущей конструкции металлургического мостового крана [1–14].
Методика. Теоретическое обоснование расчета долговечности механической системы — несущей конструкции главной балки металлургического мостового крана грузоподъемностью 50 тонн осуществлены на основе спектрального метода.
Основная часть. Вещественная функция 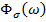 представляет собой плотность мощности напряжений процесса по спектрам частот и называется энергетическим спектром. Поставим произведение
представляет собой плотность мощности напряжений процесса по спектрам частот и называется энергетическим спектром. Поставим произведение 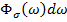 в соответствие той доле мощности рассматриваемого процесса, которая заключена в интервале от
в соответствие той доле мощности рассматриваемого процесса, которая заключена в интервале от 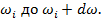 При рассмотрении случайного характера процессов, протекающих в рассматриваемой механической системе, энергетический спектр
При рассмотрении случайного характера процессов, протекающих в рассматриваемой механической системе, энергетический спектр 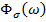 представляет собой детерминированную функцию частоты процесса. Используя формулы корреляционной функции для стационарного случайного процесса и преобразования Фурье [2, 14], запишем энергетический спектр в комплексной форме:
представляет собой детерминированную функцию частоты процесса. Используя формулы корреляционной функции для стационарного случайного процесса и преобразования Фурье [2, 14], запишем энергетический спектр в комплексной форме:
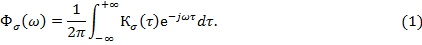
Будем определять корреляционную функцию на основе разложения плотности вероятности нагрузки на механическую систему на входе [2, 9–14] по ортонормированным полиномам Чебышева-Эрмита и будем иметь спектральную плотность
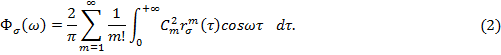
Использование спектрального метода при вероятностном синтезе обусловлено тем, что он позволяет выполнить расчет величин и распределения выходного параметра системы — величины упругопластической деформации с учетом характеристик случайного процесса нагружения.
Связь между выходными и входными параметрами механической системы имеет вид
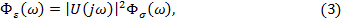
где 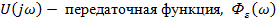 — спектральная плотность распределения упругопластической деформации,
— спектральная плотность распределения упругопластической деформации, 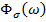 — спектральная плотность распределения действующих нагрузок (напряжений изгиба) на механическую систему.
— спектральная плотность распределения действующих нагрузок (напряжений изгиба) на механическую систему.
Результаты применения спектрального метода (3) были показаны [2] решением задач оценки работоспособности и нагруженности деталей транспортных машин и летательных аппаратов.
Тогда
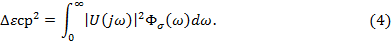
Так как кривая изменения спектральной плотности входных нагрузок представляет узкополосный процесс, то обе частотные характеристики 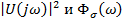 будем рассматривать в виде дробно-рациональных функций,
будем рассматривать в виде дробно-рациональных функций, 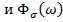 — аналитическое выражение теоретической кривой, аппроксимирующей кривую экспериментальную.
— аналитическое выражение теоретической кривой, аппроксимирующей кривую экспериментальную.
Численные значения 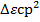 можно получить:
можно получить:
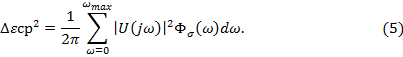
Вычислив средний квадрат распределения упругопластической деформации, определим вид кривой её распределения. Определив значения плотности вероятности закона распределения для величины упругопластической деформации при известном значении дисперсии выходного процесса. Для нормального распределения ε и Dε подставим в формулу

построим кривую дифференциальной функции распределения.
Определим вероятность опасного состояния механической системы — несущей конструкции главной балки металлургического мостового крана по нагруженности, если известен уровень допускаемых значений упругопластической деформации. Это выполняется посредством вычисления величин интегральной функции закона для выбранных значений выходного параметра в координатах P-ε.
Для нормального закона распределения случайных величин процесса используем функцию Лапласа в виде

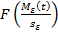 — функция Лапласа.
— функция Лапласа.
Выводы. Полученное теоретическое обоснование позволяет с известным уровнем допущения охарактеризовать вероятность появления различных по величине нагрузок на выходе сложной механической системы, тем самым решить задачу о долговечности несущей конструкции главного балки моста металлургического крана.
Заключение. Используя, на основе спектрального метода, известный уровень упругопластической деформации рассматриваемой механической системы, можно определить вероятность опасного состояния для нормального стационарного процесса нагружения. По результатам теоретического обоснования можно провести расчеты и построить интегральную функцию закона для выбранных значений выходного параметра в координатах P-ε, по которой можно будет судить о долговечности системы.
Литература:
1. Бархоткин В. В., Извеков Ю. А., Миникаев С. Р. Обзор аварий на крановом оборудовании металлургических производств. // Международный журнал прикладных и фундаментальных исследований. — Москва, РАЕ, 2013. — № 10–1. С. 9–11.
2. Бирюков М. П. Динамика и прогнозирующий расчет механических систем. // «Вышэйшая школа». — Минск, 1980. — 189 с: ил.
3. Извеков Ю. А. Анализ техногенной безопасности кранового хозяйства России. // Современные наукоемкие технологии. — Москва, РАЕ, 2012. — № 12. С. 18–19.
4. Извеков Ю. А., Кобелькова Е. В., Лосева Н. А. Анализ динамики и вопросы оптимизации металлургических мостовых кранов. // Фундаментальные исследования. — Москва, РАЕ, 2013. — № 6–2. С. 263–266.
5. Извеков Ю. А. Риск-анализ оборудования металлургических производств. Подход, концепция, анализ. Монография. — Saarbrucken, Deutschland. LAP Lambert, 2013. — 56 c.
6. Извеков Ю. А. Моделирование прогнозирования риска несущих конструкций кранов металлургического производства. // Актуальные проблемы современной науки, техники и образования. — Магнитогорск, МГТУ, 2012. № 70, Т. 1. С. 6–8.
7. Извеков Ю. А., Кобелькова Е. В., Лосева Н. А. Аналитическая оценка пластической деформации несущих конструкций металлургических мостовых кранов. — Магнитогорск, МГТУ, 2013. № 71, Т. 1. С. 48–51.
8. Извеков Ю. А. Математическое моделирование оценки упругопластической деформации несущих конструкций механических систем. // Современные тенденции в образовании и науке: сборник научных трудов по материалам Международной научно-практической конференции 31 октября 2013: в 26 частях. Часть 15; М-во обр. и науки. Тамбов: Изд-во ТРОО «Бизнес-Наука-Общество», 2013. С. 57–58.
9. Извеков Ю. А. Прогнозирование надежности несущих конструкций кранов металлургических производств. Вопросы. Гипотезы. Ответы: Наука XXI века: Коллективная монография. — Краснодар, 2013. Книга 6, часть 3, глава 9. С. 189–211.
10. Извеков Ю. А., Кузина Т. Г. Оценка упругопластической деформации на основе метода преобразования вероятностей. // Современные проблемы науки и образования. — 2013. — № 6; URL: www.science-education.ru/113–10810 (дата обращения 14.02.2014).
11. Izvekov Y. A., Dubrovsky V. V., Hamutskikh E. Y. Mathematical Modeling and Calculation of Accuracy and Durability of Mechanical Systems' Elements. // World Applied Sciences Journal 30 (1): pp. 32–34, 2014
12. Крылова Е. А., Извеков Ю. А. О подходе к оценке техногенной безопасности металлургического производства. // Успехи современного естествознания. Москва, РАЕ, 2012. — № 6. С. 32–33.
13. Извеков Ю. А. Вероятностный синтез сложной механической системы. // Молодой ученый. — 2014. — № 4(63).
14. Извеков Ю. А., Бирюков Д. А. Прогнозирование долговечности механических систем корреляционным методом. // Актуальные проблемы гуманитарных и естественных наук. — 2014. — № 3.







