Рассматривается вопрос о разрешимости краевой задачи для нелинейного функционально-дифференциального уравнения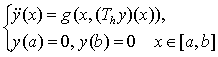 
в предположениях: оператор Немыцкого 
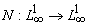, определенный равенством 
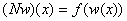, непрерывен; 
, 
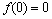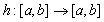— измеримая функция, такая, что существует ограниченная в существенном на 
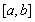производная Радона-Никодима 
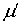функция множества 
.
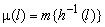Ключевые слова: краевая задача, линейный оператор, функционально-дифференциальное уравнение.
Рассмотрим вопрос о разрешимости краевой задачи для нелинейного функционально-дифференциального уравнения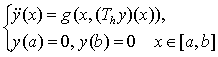
в следующих предположениях: оператор Немыцкого 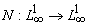, определенный равенством 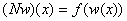, непрерывен; 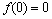, 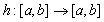— измеримая функция, такая, что существует ограниченная в существенном на 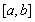производная Радона-Никодима 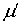функция множества .
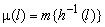Будем пользоваться следующими обозначениями:
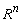— пространство 
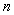-мерных вектор-столбцов с нормой 
;
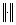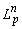- пространство суммируемых в 
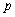–ой степени на отрезке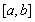
вектор-функций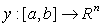 
с нормой 
, (
);
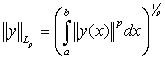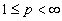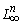— пространство ограниченных в существенном 
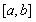на вектор-функций 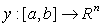с нормой 
;
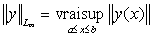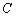— пространство непрерывных на 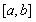вектор-функций 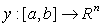с нормой 
;
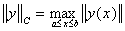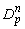— пространство таких абсолютно-непрерывных функций 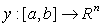, что 
, 
;
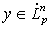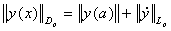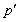— показатель степени, сопряженный с : 
;
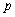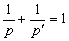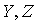— банаховы пространства с нормами 
, 
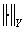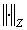соответственно;
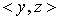— скалярное произведение в 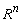, определенное равенством 
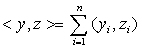, где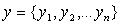 
, 
;
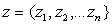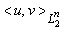— скалярное произведение в 
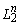, определенное равенством 
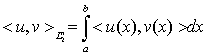и согласованное с нормой в ;
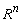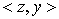— билинейная форма, заданная на 
, 
, 
;
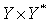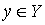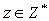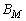— шар в 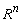радиуса 
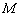с центром в нуле;
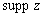— носитель суммируемой функции 
;
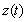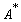— оператор, сопряженный к 
.
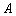Рассмотрим уравнение:
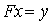(1)
с непрерывным оператором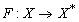 
.
Определение 1.[3, с. 21]. Оператор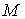 
называется коэрцитивным, если для любого 
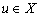выполняется неравенство 
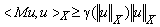, где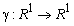 
— некоторая функция, удовлетворяющая условию 
.
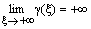Отметим, что для случая линейного ограниченного оператора, из сильной монотонности следует его коэрцитивность.
Определение 2.[3]. Оператор называется усиленно непрерывным, если он отображает слабо сходящиеся последовательности в сходящиеся.
В частности, всякий вполне непрерывный оператор является усиленно непрерывным. Обратное, вообще говоря, неверно.
В некоторых случаях утверждения, справедливые для монотонных операторов, остаются справедливыми для более широкого класса операторов, описанных в следующем определении.
Определение 3.[3, с. 267]. Оператор называется полу монотонным, если он представлен в виде суммы монотонного и усиленно непрерывного операторов.
Отметим, что полу монотонные операторы называются также монотонными в главной части [6, c. 181].
Пусть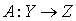 
— линейный оператор.
Определение 4. [3, с. 22]. Оператор 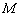называется 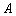-монотонным, если для любых 
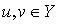выполнено неравенство 
.
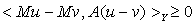Определение 5. Оператор 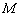называется 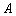-коэрцитивным, если для любого 
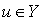выполнено условие 
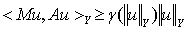, где .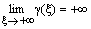
Нам потребуется следующее распространение теоремы Браудера о полу монотонном операторе, применимое и в тех случаях, когда оператор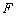 
не является полу монотонным или коэрцитивным.
Лемма 1. Пусть выполнены предположения:
а)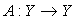 
– линейный обратимый оператор;
б)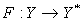 
- непрерывный оператор;
в) оператор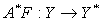 
— полу монотонен;
г) оператор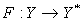 
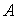- коэрцитивен.
Тогда уравнение (1) имеет хотя бы одно решение для любого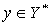 
.
Уравнение (1) эквивалентно уравнению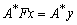 
(2)
Рассмотрим далее краевую задачу
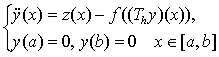(3)
в следующих предположениях:
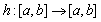— измеримая функция, такая, что существует ограниченная в существенном на 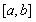производная Радона-Никодима 
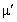функция множества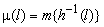 
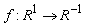удовлетворяет условиям Каратеодори и оператор Немыцкого 
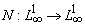, определенный равенством 
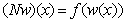, непрерывен; 
.
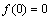Будут получены признаки разрешимости задачи (3), основанные на теореме Браудера [3].
Определение 6.1–6.2. Будем говорить, что функция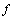 
на множестве 
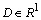: удовлетворяет условию /6А, 
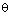/, если существует такое число 
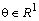, что для всех 
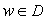выполнено неравенство 
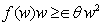; удовлетворяет условию /6Б, 
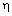/, если существует такое число 
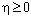, что для всех 
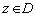выполнено неравенство 
.
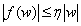Обозначим через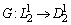 
оператор Грина краевой задачи
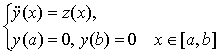(4)
Отметим некоторые свойства оператора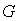 
[6, с. 79, 88]. Имеем представление
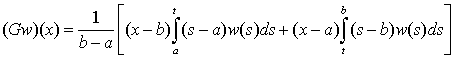(5)
Оператор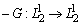 
положителен, т. е. для любого 
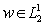имеет место неравенство
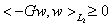(6)
Рассмотрим семейство операторов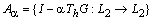 
, где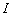 
— тождественный оператор, 
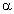— действительный параметр и 
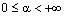. Предварительно докажем вспомогательное утверждение.
Лемма 2. Для любого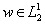 
имеет место неравенство
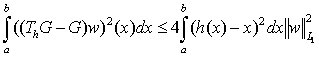. (7)
Определим оператор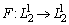 
равенством 
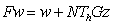и рассмотрим уравнение
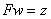(8)
Приведем одно вспомогательное утверждение.
Лемма 4. Для любого 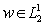имеет место неравенство 
.
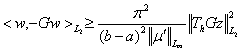Приводимое ниже утверждение позволит нам заменить исследование краевой задачи (3) исследованием уравнение (8).
Предложение 5. [1] 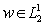является решение уравнения (8) тогда и только тогда, когда 
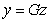является решением задачи (3).
Исследуем свойства оператора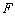 
.
Лемма 6. Пусть выполнены предположения:
а) функция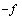 
удовлетворяет условиям /6А, 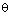/, /6Б, 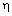/, на множестве 
;
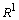б) выполнено неравенство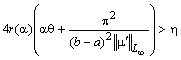 
(9)
где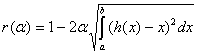 
, 
.
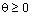Тогда оператор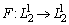 
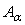-коэрцитивен и для любого 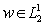имеет место неравенство 
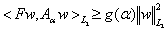(10)
где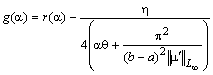
.
Следствие 7. Пусть выполнены предположения:
а) функция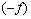 
удовлетворяет условиям /6А, 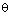/, /6Б, 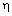/, на множестве ;
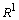б) выполнены неравенства (7) и (9).
Тогда все решения задачи (3) удовлетворяют оценке
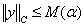(11)
где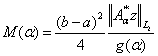 
.
Теорема 8. Пусть существует такое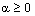 
. что выполнены условия:
а) функция 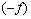удовлетворяет условиям /6А, 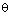/, /6Б, 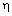/, на множестве 
;
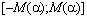б) выполнены неравенства (7), (9).
Тогда краевая задача (3) имеет решение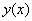 
, которое удовлетворяет оценке (11).
Доказательство. Ввиду выполнения всех предположений следствия 7 будем доказывать существование решения вспомогательной краевой задачи
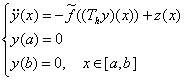(12)
удовлетворяющего оценке (11), где каратеодорева функция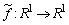 
совпадает с 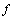на множестве 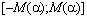, 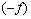удовлетворяет условиям /6А, 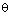/, /6Б, 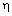/ на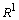 и оператор Немыцкого 
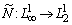, определяемый равенством 
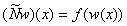, непрерывен.
Рассмотрим оператор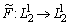 
, определенный равенством 
.
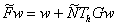Из леммы 6 следует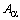 
-коэрцитивность оператора 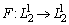, при этом оператор 
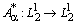обратим (см. лемму 3). Из (9) следует, что 
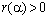. Оператор 
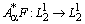полу монотонен. Действительно, непосредственно получаем представление 
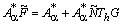(13)
Здесь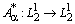 
монотонен по лемме 6. Оператор 
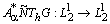вполне непрерывен, а значит, усиленно непрерывен. Итак, (13) есть представление оператора 
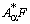в виде суммы монотонного и усиленно непрерывного, т. е. оператор 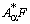является полу монотонным.
Итак, выполнены все условия леммы 1, поэтому уравнение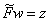 
имеет решение 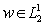, а краевая задача (12) имеет решение 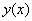, удовлетворяющее оценке (11). Тогда это 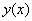является решением задачи (3). Доказательство закончено.
Литература:
1. Азбелев Н. В., Исламов Г. Г. Об одном классе функционально-дифференциальных уравнений // Дифференциальные уравнения. — 1976. — Т. 12. — № 3. — с. 417–427.
2. Азбелев Н. В., Максимов В. П. Априорные оценки решений задачи Коши и разрешимость краевых задач для уравнений с запаздывающим аргументом // Дифференциальные уравнения. 1979. — Т. 15. — № 10. — с. 1731–1747.
3. Вайнберг М. М. Вариационный метод и метод монотонных операторов., М., Наука, 1972, — 416 с.
4. Забрейко П. П., Кошелев А. И., Красносельский М. А. и др. Интегральные уравнения., М: Наука, 1968, — 448, /Сер. «Справочная математическая библиотека»/.
5. Кигурадзе И. Т., Шехтер Б. Л. Сингулярные краевые задачи для обыкновенных дифференциальных уравнений второго порядка. // Современные проблемы математики. Новейшие достижения. — М.: ВИНИТИ, 1987. — Т. 30. — с. 105–201. — /Итоги науки и техники ВИНИТИ АН СССР/.
6. Куфнер А., Фучик С. Нелинейные дифференциальные уравнения. Пер. с англ. А. Ф. Жукова. — М.: Наука, 1988. -304 с.
7. Харди Г. Г., Литтльвуд Дж. Е., Полиа Г. Неравенства, ЛКИ, 3 издание, 2008, — 456 с.
