Задачи дифракция упругих волн многониточное трубопроводе решается с помощью метода теории потенциалов. Получено численное решение.
Problems diffraction of elastic waves многониточное the pipeline dares by means of a method of the theory of potentials. The numerical decision
Двух ниточные трубопроводы имеют широкие распространения в мелиоративном и гидротехническом строительстве. В работах [1], [2] изучалась стационарная дифракция сейсмических Р- волн сжатия, SV-и SH- волны сдвига на подземном двух ниточном и многониточном трубопроводах. Основываясь на этих решениях, можем теперь решить задачу о нестационарной дифракции сейсмических волн на двух ниточном трубопроводе. Учитывая неустановившееся движение и пренебрегая массовыми силами, получим следующую систему уравнений для потенциалов j и y [1].
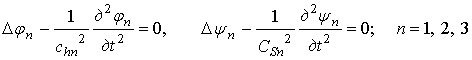 (1)
(1)
где Срп и CSn- скорости распространения волн сжатия и сдвига; значения индекса n=1, 2, 3 соответствуют грунту, трубам, и жидкости внутри труб, при этом y3=0. Согласно [2] решение задачи нестационарной дифракции (1) может быть представлено в виде суперпозиции решений задачи стационарной дифракции [2]
Djт+an2jn=0;Dyn+bn2yn=0, (2)
Где 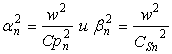 — волновые числа, b3=0;
— волновые числа, b3=0;
Cpn2 = [(ln + 2mn)/rn]112;CSn2=(mn/rn)1/2, ln и mn- постоянные параметры Ляме, rn- плотность материала.
В [1] для случая падения Рк- SV- и SH- волн перпендикулярно к оси двух ниточного трубопровода получено асимптотическое решение уравнения (2) в биполярных координатах. На основе этого решения с учетом положений [2] имеем следующие:
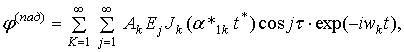
Где 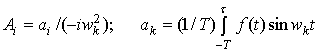 ,
,
где ак- коэффициент Фурье, определяющий форму волны для произвольного интервала времени Т; wk- частота к той форме wk=kp/T (k=1, 2, …); f(t) — акселерограмма сейсмической волны на интервале [o, T]; e0=1; ek=2; Zn — функция Бесселя первого рода; a1к*=a1к для р- волны и a1к*=b1к для SV- и SH-волн. Потенциалы волн, отраженных от труб в грунт с учетом условий Зоммерфельда [1] имеют вид:
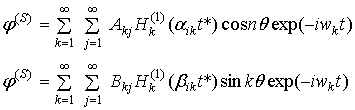 , (3)
, (3)
где Нк(1) — функция Ханкеля первого рода к-го порядка. Суммарные потенциалы волн в грунте в случае падения соответственно Р-, SV-, SH- волн:
j1=j(под)+ j(S);y1=y(S) илиj1=j(5);y1=y(под)+ y(S).
Потенциалы волн в трубах запишутся следующим образом
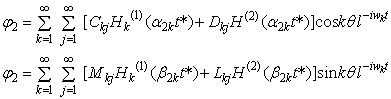 , (4)
, (4)
Где Нк(2)- функция Ханкеля второго рода.
В случае падения SH — волны сдвига в (4) останется только потенциалы y2. Потенциал скоростей жидкости
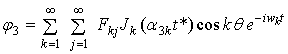 .
.
Краевые условия имеет следующий вид: на внешнем контуре труб условия идеального контакта с грунтом.
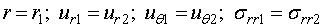
на внутреннем контуре труб при начальных жидкости
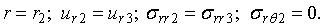
Для решения поставленной задачи использовался принцип суперпозиции. Решение (1) определяет реакцию подземных труб на последовательность нестационарных импульсов. Пусть время покоя (промежуток между импульсами) достаточно велико для того, чтобы трубы смогли вернуться в недеформированное состояния. Тогда, производя отсчет времени с момента прохода импульса (т. е., переходя к новой временной переменной t*=t-t0), определим реакцию первоначально недеформированных труб на действие одного импульса. Для численной реализации полученных формул составлена программа на языке С++.
В этом случае окружное напряжение на поверхности трубопровода сводится к следующему:
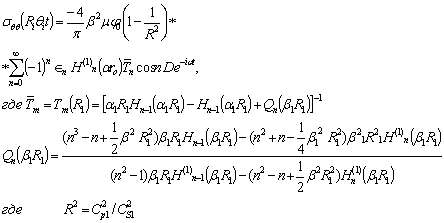
Коэффициент концентрации напряжения 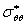 здесь определяется как отношение
здесь определяется как отношение 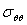 к
к 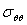 возникало бы в той же точке при условии отсутствия полости.
возникало бы в той же точке при условии отсутствия полости.
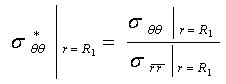 ,
,

где 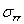 определяется как функции j (р) в виде
определяется как функции j (р) в виде
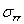 = i pj0 m a2 [H2(1)pjm((a
= i pj0 m a2 [H2(1)pjm((a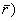 +(1-R2) Ho(1)(a
+(1-R2) Ho(1)(a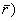 ] e-iwt
] e-iwt 
Анализ полученных результатов показывает, что динамическое давление грунта на трубы srrA практически сразу после начального момента времени набирает максимального значения, превышающее на 20 % значение s0 импульса падающей волны).
Затем с течением времени это давление снижается до значение s0 и сохраняется до момента времени t=DT/2, после чего идет практически моментальное снижение srrА сначала до нуля, а затем и до небольших отрицательных значений, не превышающих 13–160/s0, далее принимает малые положительные значение и полностью затухает к моменту времени t=DT.
Полученные численные результаты позволяют делать следующие выводы.
1. При сейсмическом воздействии взаимное влияние железобетонных труб многониточной укладки имеет место при расстоянии между ними d>4,0D и приводит к увеличению максимального динамического давления грунта на них по сравнению с одиночной трубой (явление местного резонанса) на 5–10 %.
2. Появление резонанса в многониточных трубах можно избежать, если выбирать расстояние между ними некратным, длине падающей сейсмической волны. Это явление резонанса является особенностью многониточного трубопровода и не может возникнуть в трубопроводе, уложенном в одну нитку.
3. Максимальное статическое давление грунта (smax) на трубы, уложенные в несколько ниток на расстоянии в свету d,3,0D друг от друга, меньше, чем на одиночную трубу в среднем на 10 % для крайней трубы и на 20 % для средней. При этом величина с smax возрастает с ростом параметра d, имея минимум при d=0 (трубы, уложенные вплотную) и максимум при d=3,0В, совпадающий с соответствующим значением для одиночной трубы.
Давление smax убывает с ростом коэффициента Пуассона n грунта. Наибольшее значение величины smax соответствует опиранию на фундамент, наименьшее — на спрофилированное основание с большим углом охвата. Давление smax на крайнюю трубу и на среднюю трубу практически не зависит от числа ниток.
Литература:
1. Базаров М. Б., Сафаров И. И., Шокин Ю. М. Численное моделирование колебаний диссипативно–неоднородных и однородных механических систем. — Новосибирск, Сибирское отд. РАН, 1996. — 189 с.
2. Каюмов С. С., Сафаров И. И., Распространение и дифракция волн в диссипативно-неоднородных цилиндрических деформируемых механических системах. — Тошкент: Фан, 2004, — 215с.







