Описывается методика решения задач о распространении волн в бесконечном цилиндре с радиальной трещиной. Вязкие свойства материала учитываются с помощью интегрального оператора Вольтера. Исследование проводится в рамках пространственной теории вязко упругости. Методика основана на разделении пространственных переменных и формулировании краевой задачи на собственные значения, которые решаются методом ортогональной прогонки Годунова. Получены числовые значения реальной и мнимой части фазовой скорости в зависимости от волновых чисел. При этом получено совпадение числовых результатов с известными данными.
Ключевые слова. Волна, цилиндр, трещина, интегральный оператор, дифференциальные уравнения, ядро релаксации, ортогональная прогонка, аппроксимация, частные производные, фазовая скорость, частота, коэффициент затухания.
The method solution of fasces about spreading of waves in infinite cylinder with a radial crack is described. Demptering abilities of a material are considered by means of integrated operator of Voltaire. Research is conducted within the limits of the spatial theory of viscously elasticity. The technique is based on division of spatial variables and formulation of an edge task on the own values which are edved by the method of orthogonal prorace of Godunov. Numerical values of a real and imaginary part of phase speed depending on wave numbers are received. Coincidence of numerical results with known data is received at this.
Keywords. Wave, cylinder, crack, integrated operator, differential equations, relaxation kernel, orthogonal prorace, approximation, private coefficient of derivatives, phase speed, frequency, attenuation.
Введение. Распространение волн в цилиндре было предметом многочисленных теоретических и экспериментальных исследований. Возможность выразить характеристики волнового поля в цилиндре через хорошо исследованные специальные функции впервые отмечались в работах Похгаммера [1] и Кри [2]. Для упругого слоя (двухмерная задача) аналогичные результаты получены Рэлеем [3]. Первые численные результаты, относящиеся к некоторым характеристикам нормальных волн в слое, содержатся в работе Лэмба [4]. Распространение волн в сплошном цилиндре исследовано в работе Гринченко [5]. Многие строительные и машиностроительные конструкции, работающие в динамических условиях, состоят из деформируемых тел, обладающих вязкоупругими (демпфирующими) свойствами. Демпфирующая способность материала играет огромную роль в динамическом поведении конструкции. Она приводит к значительному ослаблению собственных колебаний, существенному понижению амплитуд при вынужденных колебаниях и сглаживанию напряжений в зоне концентрации при колебаниях. Оценить эту способность, можно лишь поняв природу поглощения энергии при колебаниях. В работе рассматриваются вопросы распространения гармонических волн в пространственном цилиндресрадиальной трещиной с учетомдемпфирующей способности материала.
Постановки задачи. Рассматривается распространение свободных волн в бесконечном цилиндре с радиальной трещиной внешнем и внутреннем радиусам 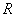 и
и 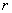 соответственно. Задача распространения гармонических волн в бесконечном упругом цилиндре с радиальной трещиной ставится в цилиндрических координатах и приводятся к системе шести дифференциальных уравнений, разрешенных относительно первой производной по радиальной координате:
соответственно. Задача распространения гармонических волн в бесконечном упругом цилиндре с радиальной трещиной ставится в цилиндрических координатах и приводятся к системе шести дифференциальных уравнений, разрешенных относительно первой производной по радиальной координате:
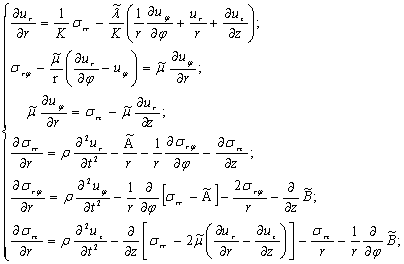 (1)
(1)
Где 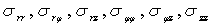 — соответсвенно компоненти тензора напряжений,
— соответсвенно компоненти тензора напряжений, 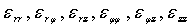 — соответственно компоненти тензора деформаций;
— соответственно компоненти тензора деформаций; 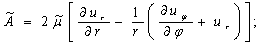
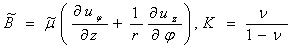 ,
, 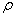 -плотность,
-плотность, 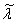 и
и 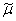 - операторный модуль упругости, которые имеют вид:
- операторный модуль упругости, которые имеют вид:
 (2)
(2)
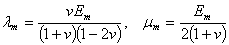 — мгновенные модули упругости;
— мгновенные модули упругости; 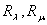 - ядро релаксации; принимаем интегральные члены в (2) малыми, тогда функции
- ядро релаксации; принимаем интегральные члены в (2) малыми, тогда функции 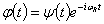 , где
, где 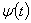 -медленно меняющаяся функция времени,
-медленно меняющаяся функция времени, 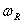 -действительная константа. Далее применяя процедуру замораживания [6], заметим соотношения (2) приближенными вида
-действительная константа. Далее применяя процедуру замораживания [6], заметим соотношения (2) приближенными вида
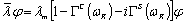 ,
, 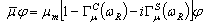 .
.
Здесь 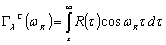 ,
, 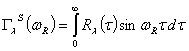 ,
,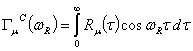 ,
,  — соответственно, косинус и синус образы Фурье ядра релаксации материала. В качестве примера вязкоупругого материала примем трех параметрических ядро релаксации
— соответственно, косинус и синус образы Фурье ядра релаксации материала. В качестве примера вязкоупругого материала примем трех параметрических ядро релаксации 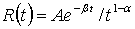 , обладающее слабой сингулярностью [9].
, обладающее слабой сингулярностью [9]. 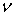 — коэффициент Пуассона.
— коэффициент Пуассона.
Краевые условия задаем в виде:
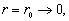
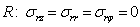 (3)
(3)
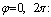

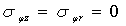 (4)
(4)
Условия (3) при r= 0 в физическом плане можно интерпретировать как результат предельного перехода от полого цилиндра со свободной внутренней поверхностью к сплошному, при стремлении внутреннего радиуса к нулю.
В случае бегущих гармонических волн вдоль оси z, решение краевой задачи (1), (2), (4) допускает разделение переменных:
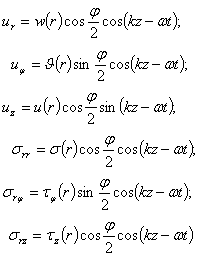 (5)
(5)
где 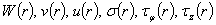 — амплитуды колебаний которые являются функцией радиальной координаты;
— амплитуды колебаний которые являются функцией радиальной координаты; 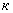 — комплексная волновая число;
— комплексная волновая число; 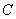 — комплексная фазовая скорость;
— комплексная фазовая скорость; 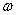 — комплексная частота.
— комплексная частота.
Для выяснения их физического смысла рассматриваем случаи;
1) 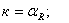
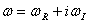 (
(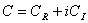 ) — тогда решение (5) имеет вид синусоиды по z, амплитуда которой затухает по времени;
) — тогда решение (5) имеет вид синусоиды по z, амплитуда которой затухает по времени;
2) 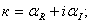
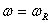 (
(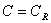 )-тогда решение (5) имеет вид синусоиды по t, амплитуда которой затухает по z;
)-тогда решение (5) имеет вид синусоиды по t, амплитуда которой затухает по z;
С учетом (5), задача (3), (4), (5) преобразуется в спектральную краевую задачу для системы обыкновенных дифференциальных уравнений с комплексными коэффициентными:
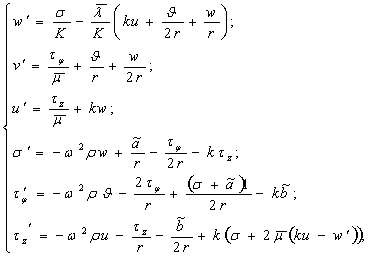 (6)
(6)
Где 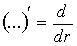 ,
, 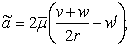
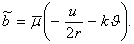
С краевыми условиями при 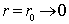 ,
,  ,
, 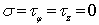 (7)
(7)
Отметим, что выбор краевых условий на гранях щели в виде (4) обусловим в первую очередь возможностью разделения переменных по координатам 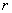 и
и 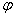 , что существенно упрощает решение исходной задачи. Разделение перемещенных возможно также в случае следующих краевых условий:
, что существенно упрощает решение исходной задачи. Разделение перемещенных возможно также в случае следующих краевых условий:
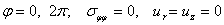 (8)
(8)
Действительно, выполняют замену переменных так, чтобы удовлетворяли условия (8).
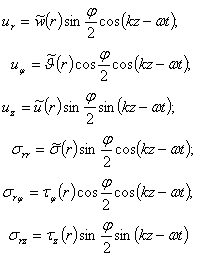
получаем спектральную краевую задачу
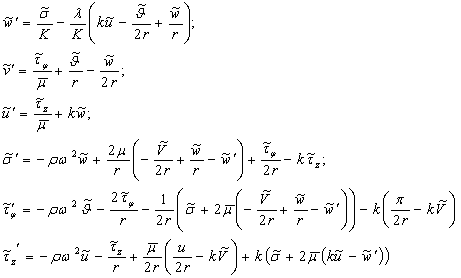
с краевыми условиями
 (10)
(10)
Нетрудно видеть, что задача (9), (10) сводится к задачу (6), (7) с помощью замены
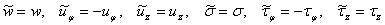
Таким образом, сформулирована спектральная краевая задача (7), описывающая распространение гармонических волн в бесконечном цилиндре с радиальной трещиной.
Краевая задача для системы уравнений в частных производных (7) может быть сведена к краевой задаче для системы обыкновенных дифференциальных уравнений с помощью метода прямых, что позволит использовать в решении программный аппарат метода ортогональной прогонки. Согласно методу прямых прямоугольная область определения функции основных неизвестных покрывается прямыми, параллельными оси r и равномерно отстоящими друг от друга. Решение ищется только на этих прямых, а производная по направлению φ, заменяется приближенными конечными разностями. Используемые аппроксимирующие формулы второго порядка для первой и второй производной имеют вид:
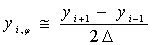
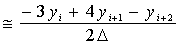
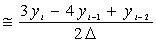 (8)
(8)
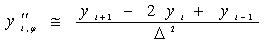 (9)
(9)
Где i изменяется от 0 до 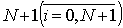 ,
, 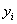 — проекция неизвестной функции на прямую с номером i; Δ — шаг разбиения по координате φ. В результате дискретизации вектор основных неизвестных общей размерности 6N может быть записан в виде:
— проекция неизвестной функции на прямую с номером i; Δ — шаг разбиения по координате φ. В результате дискретизации вектор основных неизвестных общей размерности 6N может быть записан в виде:
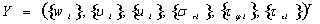
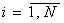 (10)
(10)
Центральные разности (8), (9) используются для внутренних прямых (1 <i<N),левая и правая разности (9), (10) позволяют учесть краевые условия по φ. Впервом случае производная по φ вправых частях системы уравнений (7) выражается по формулам: 1 <i<N
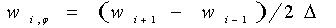 ,
, 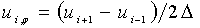
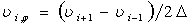 ,
, 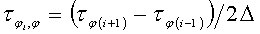 , (11)
, (11)
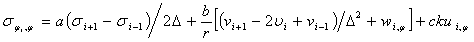
Краевые условия при 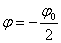 учитываются в уравнениях, соответствующих прямых i=1. Для основных неизвестных, не входящих в краевые условия, wi, vi, uiиспользуются правые разности:
учитываются в уравнениях, соответствующих прямых i=1. Для основных неизвестных, не входящих в краевые условия, wi, vi, uiиспользуются правые разности:
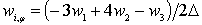 ,
, 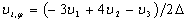 , (12)
, (12)

Аналогичным образом представляются производные для прямой с номером i =N, учитывающие краевые условия при 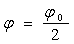 . Единственное отличие состоит в замене правых конечных разностей левыми: i=N:
. Единственное отличие состоит в замене правых конечных разностей левыми: i=N:
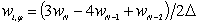 ,
, 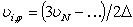 ,
,
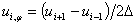 ,
, 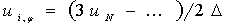 , (13)
, (13)
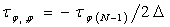 ,
, 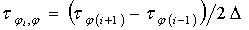 ,
,
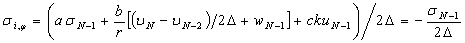
Число прямых можно уменьшить вдвое, если использовать условия анти симметрии поперечных колебаний цилиндра.
Таким образом, исходная спектральная задача (6) с помощью дискретизации координаты φ по методу прямых сведена к канонической задаче (11), (12) и (13).
Численные результаты. Решение задачи (6) выполнялось методом ортогональной прогонки Годунова [7]. Решение поставленной задачи на определение скорости распространения волн и формы колебаний осуществляется методом Мюллера без выделения комплексного параметра С (комплексной фазовой скорости) или 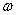 - комплексной частоты. На каждом шаге итерационного уточнения величины С (или
- комплексной частоты. На каждом шаге итерационного уточнения величины С (или 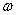 ) методом ортогональной прогонки решается краевая задача (6), фазовая скорость и собственные числа определяются из условия равенства нулю определителя системы, вычисляемого методом Гаусса. Безразмерные величины в постановке задачи выбраны таким образом (
) методом ортогональной прогонки решается краевая задача (6), фазовая скорость и собственные числа определяются из условия равенства нулю определителя системы, вычисляемого методом Гаусса. Безразмерные величины в постановке задачи выбраны таким образом (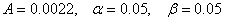 ), что реальные и мнимее части комплексная скорость сдвига Сs, плотность ρ и внешний радиус R имеют единичные значения.
), что реальные и мнимее части комплексная скорость сдвига Сs, плотность ρ и внешний радиус R имеют единичные значения.
На рис.1. изображено дисперсионных кривых первых двух мод колебаний в бесконечном упругом цилиндре с радиальной трещинной (кривая 1 и 2). Для сравнения на этом рисунке показано зависимость от волнового числа фазовой скорости изгибной моды колебаний слишком цилиндра (кривая 3) без тела. Решение СR совпадаетсрешением найдено ранее Похгомером и Кри с помощью специальных функций разницей до 10–15 %.

Рис. 1. Изменение реальные и мнимые части частоти колебаний.
Отметим характерные особенности кривой 3 в нуля фазовая скорость равна нулю, а на бесконечности приближается к скорости волны Релея для полупространства. В случае цилиндра с радиальной трещиной первые мода имеет частоту отсечки, а фазовая скорость стремится к бесконечности. При больших волновых числах предельная фазовая скорость этой моды также совпадает со скоростью волны Рэлея. На частоте отсечке осевая перемещения равны нулю к колебания цилиндра проходит в плоском деформированным состоянии.
Учет вязкоупругих свойств материала позволяет снижать амплитуды распространения волн на 10–15 %, а также позволяет оценить демпфирующие способности системы в целом.
Литература:
1. Pochhammer L. Über die Fortpflanzung segechwindigkeiten schwingungen in einem unbergrawzten isotropen kreiscylinder. — Y.reine und angew. Math., 1876. 81, № 4, — S. 324–336.
2. Chree C. Longitudinal vibrations of a corcablar bar. –Quart. J. Pure and Appl. Math, 1886, 21, N 83184, — P. 287–298.
3. Каюмов С. С., Сафаров И. И. Распространение и дифракция волн в диссипативно — неоднородных цилиндрических деформируемых механических системах. Ташкент: Фан, 2004 г. — 250 с.
4. Носирова Ш. Н., Сафаров И.И, Каюмов С. С. Гармонические волны и их применение в практике. — Т.: Фан, 2008. — 308 с.
5. Гриченко В. Т., Мелешко В. В. Гармонические колебания и волны в упругих телах, К.: Наукова думка, 1981, — 283 с.
6. Кравчук А. С., Майборода В. П., Уржумаев Ю. С. Механика полимерных и композиционных материалов: экспериментальные и численные методы. –М.: Наука. 1985, — 304 с.
7. Годунов С. К. Уравнения математической физики. — М.: Наука, 1971. — 416 с.
8. Уайт. Поверхностные упругие волны. — Тр. института инженеров по электротехнике и радиоэлектронике. 1970, 58, № 8, — С. 68–110.







