Сжатие аудиоданных является актуальной на сегодняшний день проблемой. Существует две причины, обуславливающие необходимость компрессии аудиоданных: экономия памяти при хранении аудиоинформации, низкая пропускная способность каналов передачи цифровой информации на расстояние. Применение компрессии эффективно решает обе вышеуказанные проблемы.
Сжатие данных — алгоритмическое преобразование данных, производимое с целью уменьшения их объёма. Применяется для более рационального использования устройств хранения и передачи данных. Сжатие основано на устранении избыточности, содержащейся в исходных данных.
Для обеспечения требуемых параметров передачи речевых (музыкальных) сигналов по современным низкоскоростным цифровым каналам связи и для обеспечения заданной помехоустойчивости необходимо применять высокоэффективные алгоритмы компрессии данных.
Канал передачи характеризуется таким понятием как емкость канала:
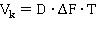
А сигнал — объемом (сигнала):
.
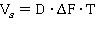Обе вышеуказанные характеристики включают в себя динамический диапазон D, ширину канала (спектра сигнала)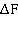 
и время прохождения сигнала T.
Для уменьшения динамического диапазона применяют цифровые аудио-компрессоры. Для улучшения спектральной эффективности применяют цифровые фильтры, ограничивающие спектр выходного сигнала кодера (по критерию Найквиста).
Помимо прочего для обеспечения заданной скорости передачи информации применяют кодеры основанные на принципах устранения избыточности (коды Хаффмана). Суть которого заключается в следующем: коды базирующиеся на принципе присвоения более вероятным значениям амплитуд кодовых слов меньшей длинны, нежели маловероятным.
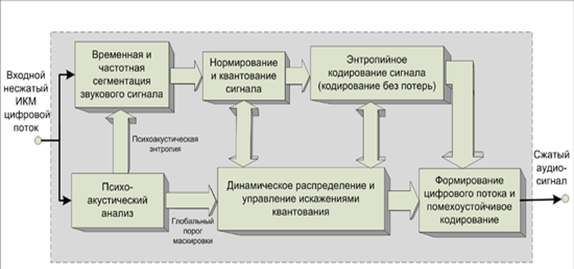
На рис.1 представлена обобщенная структурная схема кодера, применяемого в стандартах передачи аудиоданных по цифровым каналам связи. Рассмотрим как происходит устранения выше описанных видов избыточности.
Рис.1. Структура кодера сжатия аудиоданных с потерями
Исходный цифровой звуковой сигнал разделяется на частотные поддиапазоны и сегментируется по времени в блоке временной и частотной сегментации.
Длина кодируемой выборки зависит от формы временной функции звукового сигнала. При отсутствии резких выбросов по амплитуде используется так называемая длинная выборка, обеспечивающая высокое разрешение по частоте. В случае же резких изменений амплитуды сигнала длина кодируемой выборки резко уменьшается, что дает более высокое разрешение по времени. Решение об изменении длины кодируемой выборки принимает блок психоакустического анализа, вычисляя значение психоакустической энтропии сигнала.
После сегментации сигналы частотных поддиапазонов нормируются, квантуются и кодируются. В наиболее эффективных алгоритмах компрессии кодированию подвергаются не сами отсчеты выборки звукового сигнала, а соответствующие им коэффициенты МДКП. (между коэффициентами разброс меньше)
Учет закономерностей слухового восприятия звукового сигнала выполняется в блоке психоакустического анализа. Здесь по специальной процедуре для каждого частотного поддиапазона рассчитывается максимально допустимый уровень искажений (шумов) квантования, при котором они еще маскируются полезным сигналом данного поддиапазона.
Блок динамического распределения бит в соответствии с требованиями психоакустической модели для каждого поддиапазона кодирования выделяет такое минимально возможное их количество, при котором уровень искажений, вызванных квантованием, не превышал порога их слышимости, рассчитанного психоакустической моделью.
В данной статье будут рассмотрены функциональные схемы алгоритмов компрессии аудиоданных, на основе µ-, А-законов.
Функциональная схема алгоритма компрессии на основе А-уровневого закона компрессии представлена на рис.2.
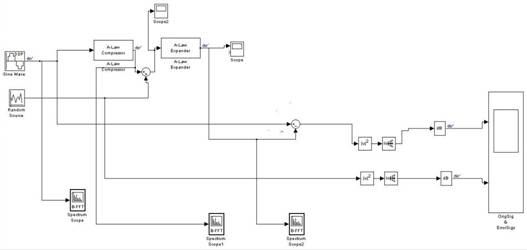
Рис.2. Функциональная схема алгоритма компрессии на основе А-уровневого закона компрессии
На вход компрессора поступает сигнал (дискретный синус). После компрессии сигнал поступает на сумматор, где на второй вход сумматора подаются шумы, тем самым имитируется аддитивный шум канала передачи. Далее сигнал с шумом поступает на вход экспандера, на выходе мы получаем восстановленный сигнал. Затем восстановленный и исходный сигнал подаются на сумматор, после которого просматривается спектральная мощность шума. В результате получаем следующие графики (рис.3).
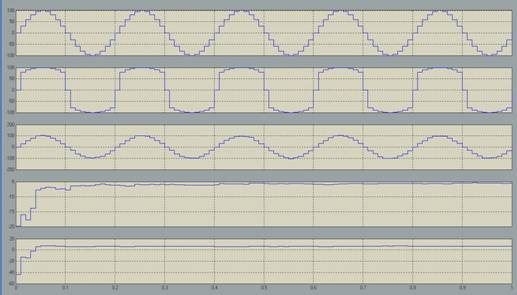
Рис.3. Результаты моделирования (А=87,6)
На рис.3. представлены следующие графики: 1-исходный сигнал, 2-сигнал прошедший через компрессор, 3-восстановленный сигнал, 4-мощность шума на выходе генератора шума, 5-мощность шума после экспандера.
Аналогичные результаты моделирования можно получить для µ- уровневого закона компрессии.
По результатам моделирования, можно сделать следующие выводы:
1. Действительно, представленные модели являются компрессорами. Это видно из сравнения первой и второй осциллограмм, поскольку количество дискретных уровней уменьшилось.
2. Из сравнения мощностей шума вытекает, что в процессе восстановления сигнала мощность аддитивного шума увеличивается.
Интересным для рассмотрения являются также спектры сигналов, представленные на рис.4.
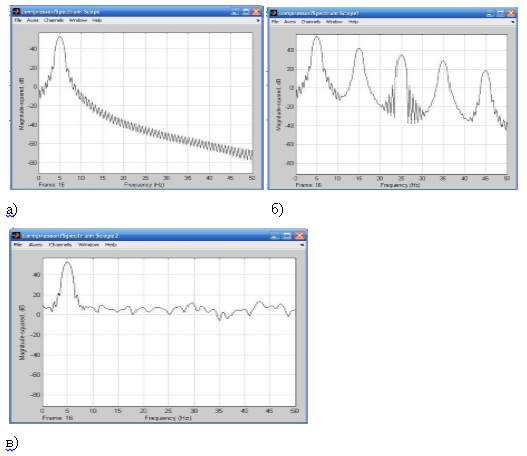
Рис.4. Спектры сигналов: а) исходного сигнала, б) сигнала на выходе компрессора, в) сигнала на выходе экспандера
На данном примере можно увидеть, как спектр сигнала меняет свою форму, проходя через компрессор и экспандер. Видно, что исходный сигнал имеет максимум на частоте 5кГц. После компрессии форма сигнала исказилась (вследствие нелинейной обработки), поэтому в спектре появились составляющие с кратными частотами. После восстановления сигнала остался один максимум на частоте 5кГц, но остальной спектр имеет меньший наклон, что отображает влияние шумов канала и шумов квантования.
Рассмотрим процессы происходящие в схеме изображенной на рис.5.
С помощью данной схемы происходит сравнение трех видов сигналов:
1. Равномерное квантование –деквантование (линейное преобразование);
2. Квантование PCM-A — A-PCM (нелинейное преобразование);
3. Квантование PCM-µ — µ-PCM(нелинейное преобразование).
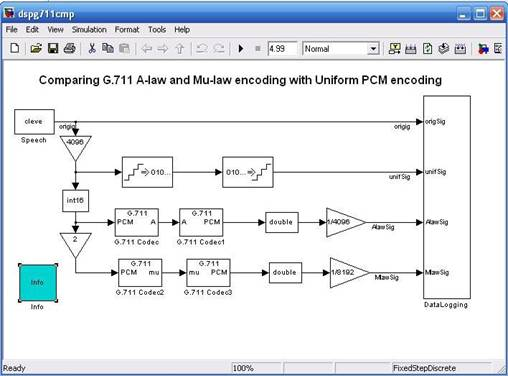
Рис.5. Схема сравнения А и µ кодирования с унифицированной ИКМ кодированием
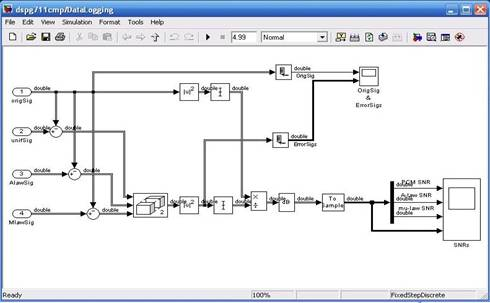
Рис.6. Содержание блокаDataLogging
Итак, рассмотрим функционирование данной схемы. Сигнал, имитирующий речь, с блока cleve поступает на «ветвь» линейного преобразования после чего подается на вход unifSig (вход 2) блока DataLogging. Также исходный сигнал подается на «ветви» нелинейного преобразования (кодеки ИКМ — А (ИКМ — µ) и А — ИКМ (µ — ИКМ)) затем сигналы поступают, соответственно, на вход AlawSig (вход 3) и MawSig (вход 4) блока DataLogging. В данном блоке происходит следующее. Из сигнала поступившего на вход 2 вычитается «оригинальный» сигнал, тоже самое происходит с 3 и 4 входами. Полученные на трех входах данные записываются в стег. После стега вычисляется дисперсия ошибки. Тоже самое происходит и с «оригинальным» сигналом. Затем мощность ошибки делится на дисперсию оригинального сигнала и полученные данные выводятся на график (рис.7).
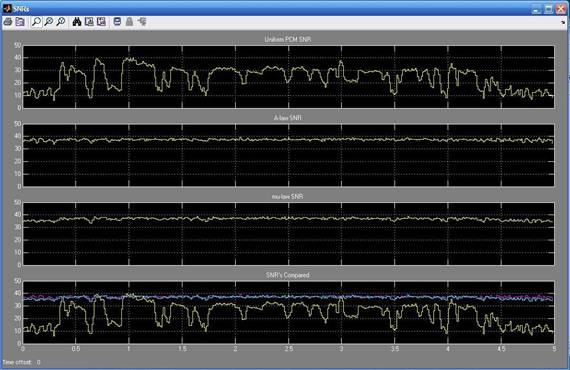
Рис.7. Графики на выходе блока DataLogging
На первом графике мы видим отношение сигнал/шум равномерного квантования. На 2 и 3 сигналы А и µ компрессоров. На 4 их совокупность. Из рис.7 можно вынести следующее: после прохождения через А и µ компрессоров отношение становится постоянным и имеет значение порядка 35дБ. Применение компрессии позволяет сделать отношение сигнал/шум постоянным и сузить динамический диапазон.
На рис.8 показан оригинальный сигнал (верхний) и дисперсии шумов квантования (нижний).
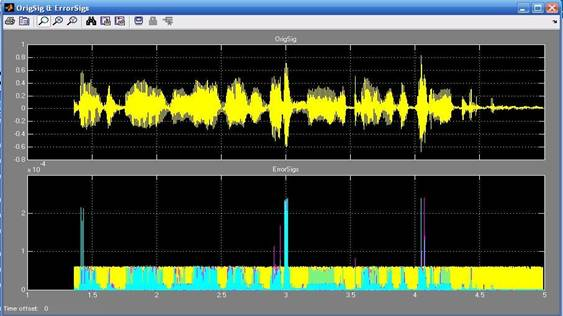
Рис.8. Сигнал на выходе блока OrigSig&ErrorSig
На нижнем графике постоянной амплитудой (желтый цвет) изображена дисперсия шума квантования равномерно квантованного сигнала (прошедшего по первой ветви). Также мы видим скачки, вызванные большими амплитудами оригинального сигнала. За счет переменного шага квантования добиваемся снижения динамического диапазона при постоянном значении сигнал/шум (см. график 2 и 3 на рис.7).
Проанализировав работу последней схемы, можно прийти к следующему заключению. Для сигналов малой амплитуды характеристика сжатия имеет более крутой фронт, чем для сигналов большой амплитуды. Следовательно, изменение данного сигнала при малых амплитудах затронет большее число равномерно размещенных уровней квантования, чем тоже изменение при больших амплитудах. Характеристика сжатия эффективно меняет распределение амплитуд входного сигнала, так что на выходе системы сжатия уже не существует превосходства сигналов малых амплитуд (т. е. распределение из нормального стремиться к равномерному).
В данной статье были рассмотрены основы цифровой компрессии аудиоданных. В результате моделирования было установлено, что в результате применения сжатия с потерями, действительно восстановить данные полностью невозможно, происходит их частичная потеря. В спектре восстановленного сигнала появляются боковые лепестки. Так же было установлено, что при наличии шума в канале передачи, после восстановления шумы становятся сильнее.
Так же следует отметить следующую особенность человеческого слуха. Резкие скачки человек не успевает отследить, а к сигналу малой амплитуды прислушивается. За счет переменного уровня шага квантования добиваются маскировки шумов квантования мощным сигналом (постоянства соотношения с/ш).
Везде, где качество звука не должно в точности соответствовать оригиналу и где в будущем наверняка не потребуется серьезная обработка хранимых данных, использование формата сжатия с потерями вполне допустимо. Не всякому захочется каждый час вставлять в CD привод новый музыкальный диск, если объем винчестера составляет десятки гигабайт. Куда как проще записать музыку, например, в mp3 на винчестер или CD-ROM и слушать оттуда.
Литература:
1. Бернард Скляр Цифровая связь. Теоретические основы и практическое применение [Текст] // М.: Издательский дом — «Вильямс», 2003. -1104с., ил.
2. Хаясака К. Г. Электроакустика [Текст] // М.: «Мир», 1982. -246с.
3. Алдошина И. А. Основы психоакустики [Электронный ресурс] // подборка с сайта www.625.net (доступ свободный) — Яз. рус.
4. Бенин М. С., Подунов А. С. Звукотехника [Текст] // М.: Издательство ДОСААФ СССР, 1976.-159с.
5. Римский-Корсаков А. В. Электро-акустика [Текст] // М.: Издательство «Связь», 1973.-272с.
6. Сапожков М. А. Электро-акустика [Текст] // М.: Издательство «Связь», 1978.-272с.
7. Соболевский А. Г. Почему появились искажения? [Текст] // М.: «Радио и связь», 1985. -104с.
8. Дьяконов В. П. MATLAB 6.5 SP1/7 + Simulink 5/6. Основы применения. Серия «Библиотека профессионала» [Текст] // М.: СОЛОН-Пресс, 2005. -800 с.
9. Мартынов Н. Н. Введение в MATLAB 6 [Текст] // M.:КУДИЦ- ОБРАЗ, 2002. -352 с.
10. Солонина А. И., Улахович Д. А., Арбузов С. М., Словьёва Е. Б. Основы цифровой обработки сигналов [Текст] // СПб.: БХВ-Петербург, 2005. -768 с.
