Разрешимость транспортной задачи по критерию времени

Одной из целей обучения математике является формирование умений строить математические модели простейших реальных явлений, как средство реализации этой цели является метод математического моделирования.

Математическое моделирование находит применение при решении транспортных задач. Это задачи определения плана перевозок груза из данных пунктов отправления в заданные пункты назначения.

Математическая модель транспортной задачи является математической моделью задачи линейного программирования. Среди множества решений системы ограничений необходимо найти такое неотрицательное решение, при котором целевая функция принимала бы минимальное значение.

Процесс моделирования транспортной задачи состоит из трех этапов. Наиболее ответственным и сложным является первый этап — построение математической модели. Оно осуществляется логическим путем на основе анализа изучаемого процесса и требует умения описать процесс на языке математики. Второй этап — этап решения задачи в рамках математической теории можно еще назвать этапом математической обработки формальной модели. Именно на этом этапе применяются все математические методы (логические, алгебраические, геометрические и т. д.) для формального вывода следствий из исходных допущений модели. На стадии математической обработки рассматриваются абстракции. Этот этап представляет собой дедуктивное ядро моделирования.

На последнем этапе моделирования полученные выводы проходят через еще один процесс перевода — с языка математики обратно на естественный язык.

Как мы уже отметили, в общей постановке транспортная задача состоит в отыскании оптимального плана перевозок некоторого однородного груза с баз потребителям.

Различают два типа транспортных задач: но критерию стоимости (план перевозок оптимален, если достигнут минимум затрат на его реализацию) и по критерию времени (план оптимален, если на его реализацию затрачивается минимум времени). Задача по критерию времени возникает при перевозке срочных грузов. Как и в обычной транспортной задаче, имеется m поставщиков с запасами однородного груза в количестве а₁,а₂,..., а_m и n потребителей, которым этот груз должен быть доставлен в объемахb₁, b₂,b_п. Известныt_ij, i — 1,2,..., m;j = 1, 2,...,n — интервалы времени, за которые груз доставляется от каждого i-го поставщика каждомуj-му потребителю. Требуется составить такой план перевозок груза, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и наибольшее время доставки всех грузов является минимальным.

Составим математическую модель этой задачи. Обозначим x_ij — объем перевозимого груза отi-го поставщикаj-му потребителю. Система ограничений задачи не отличается от системы ограничений обычной транспортной задачи. Пусть X = (Х_ij), i — 1, 2,..., т; j = 1, 2,.... n — некоторое опорное решение задачи. Запишем целевую функцию задачи. Обозначим через Т(Х) наибольшее значение элементов матрицы Т(t_ij),i= 1, 2,..., m, j = 1, 2,..., п, соответствующих клеткам таблицы, занятым опорным решением: Т(Х) = 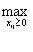{t_ij}. Таким образом, за время Т(Х) план перевозок будет выполнен полностью.

Математическая модель транспортной задачи по критерию времени имеет вид:

Т(Х) = 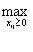{t_ij }→min,       

= a_i, i = 1, 2,...,m,      

x_ij =b_j, j = 1, 2,..., n,    

x_it ≥ 0,i = 1, 2,...,m; j = 1, 2,...,n.

Задача решается в следующем порядке. Находится начальное опорное решение X₁. Определяется значение целевой функции T(X₁) = 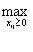{t_ij} =t. Все свободные клетки, которым соответствуют значения t_ij> Т(Х₁), исключаются из рассмотрения (перечеркиваются). Занимать эти клетки нецелесообразно, так как увеличится значение целевой функции. Чтобы уменьшить ее значение, необходимо освободить клетку (l₁,k₁), в которойt_ij достигает максимума. Для этого строят так называемые разгрузочные циклы, которые могут включать в свой состав несколько свободных клеток. В каждом разгрузочном цикле, начиная с разгружаемой клетки (l₁,k₁), расставляются поочередно знаки "+" и "-" и осуществляется сдвиг на величину 0 = min {x_ij}. Если удается эту клетку разгрузить, то она исключается из рассмотрения (зачеркивается). Получается новое опорное решениеХ₂, на котором значение целевой функции меньше, чем на Х₁. Далее снова пытаются разгрузить клетку, соответствующую Т(Х₂) = 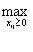{t_ij} = t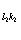.Процесс продолжается до тех пор, пока возможность разгрузить соответствующую клетку не исчезнет.

Найти минимальное время на осуществление всех перевозок для следующей задачи:

Решение. Составим начальное опорное решение Х₁ методом северо-западного угла Максимум целевой функции:

T(X₁) = 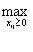{13, 8, 7, 9, 5, 10, 4} = 13

достигается в клетке (1, 1). Перечеркнем клетки (4, 1) и (4, 3), в которых время доставки груза t₄₁ = 19 и t₄₃ = 14 больше Т{Х₁) = 13.

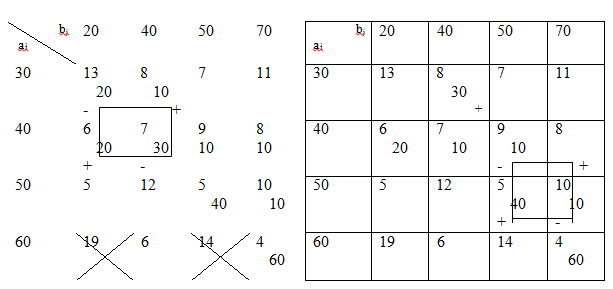
Для улучшения решения разгружаем клетку (1, 1) с помощью цикла (2, 1),(1, 1), (1,2), (2, 2). В означенном цикле находим θ = min {20, 30} = 20. Осуществляя сдвиг по циклу, получаем второе опорное решение Х₂

Максимум целевой функции на этом опорном решении Т(Х₂) =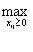 {8, 6, 7, 9,5, 10, 4} = 10 достигается в клетке (3, 4). Перечеркиваем клетки (1, 1), (1, 4) и (3, 2), в них времяt_n = 13, t₁₄ = 11 и t₃₂= 12 больше, чем Т(Х₂) = 10. Разгружаем клетку (3, 4) с помощью цикла (2, 4), (3, 4), (3, 3), (2, 3). В означенном цикле находим 9= min {10, 10} = 10. Осуществляя сдвиг по циклу, получаем третье опорное решение Х₃:

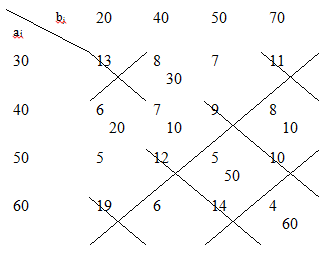
Максимум целевой функции на этом опорном решении Т(Х₃) =

= max {8, 6, 7, 8, 5, 4} = 8 достигается в клетках (1, 2) и (2, 4). Перечеркиваем _Xij> О

клетки (2, 3) и (3, 4), в которых время больше, чем Т(Х₃) = 8. С помощью оставшихся невычеркнутых клеток разгрузить клетки (1, 2) и (2, 4) не удается, поэтому Х₃ является оптимальным решением.

Ответ: Т(Х) = 8 при Х* = .

Литература:

1.         Акимова И. В., Ермолаева Е. И. Использование специальных программных средств в математическом моделировании// В мире научных открытий. 2012. № 5.4. С. 85–96.

2.         Акулич И. Л. Математическое программирование в примерах и задачах: Учебное пособие. 3-е изд., — СПб.: «Лань», 2011.-352с.

3.         Ермолаева Е. И. Проблемы усвоения математических знаний студентами технических вузов// Актуальные проблемы гуманитарных и естественных наук. 2010. № 7.- С. 270–272.

4.         Ермолаева Е. И. Математическое моделирование физических процессов в теории вероятностей// Актуальные проблемы гуманитарных и естественных наук. 2010. № 10. С. 13–15

5.         Крымская Ю. А., Титова Е. И., Ячинова С. Н. Построение математических моделей в прикладных задачах// Молодой ученый. 2013. № 12 (59). С. 3–6.