Разработанная математическая модель системы «человек-одежда-среда» позволяет разработать рациональную конструкцию и подобрать материалы пакета одежды, предназначенной для эксплуатации в жарких климатических условиях по значениям физиологических характеристик тела человека, параметров пододежного пространства, пакета одежды и окружающей среды, исходя из допустимого значения температуры кожи человека.
Designed mathematical system model «person-overalls-ambience» allows to develop the rational design and select the material of the package of the special cloth, intended for usage in hot climatic condition on importance’s of the physiological features of the person, parameter on clothes space, package of the overalls and surrounding ambiences, coming from possible importance of the temperature of the skin of the person.
При проектировании одежды, предназначенной для эксплуатации в условиях сухого жаркого климата при значительном изменении условий внешней среды с одной стороны, и при широком варьировании тепло — и влагофизических свойств материалов одежды с другой, возникают значительные трудности, связанные с учетом реакций человеческого организма на изменение условий внешней среды и необходимостью проведения длительного направленного эксперимента по подбору материалов одежды. Кроме того, возможны экстремальные сочетания условий внешней среды и одежды, при которых эксперименты вообще невозможны, т. к. они связаны с опасностью для здоровья человека (ухудшение самочувствия, возможность получения теплового удара и т. д.).
При решении подобных вопросов в мировой и отечественной практике в последнее время широко и с успехом применяется метод математического моделирования на ЭВМ. Математическое моделирование — это метод исследования физических явлений с помощью построения их математических моделей.
Однако, не всегда можно создать математическую модель в узком смысле этого слова. Так, при изучении очень сложных динамических систем и объектов с большим количеством параметров; связанных между собой нелинейно, затруднительно получить зависимость выходных показателей от входных воздействий и, тем более, от изменения параметров самой системы.
Выход из создавшегося положения был найден с переходом от математических моделей к имитационным. Имитационное моделирование на ЭВМ обладает значительно большими возможностями по исследованию сложных объектов и систем с нелинейными связями. Имитировать — это означает вообразить, постичь суть явления, не прибегая к экспериментам на реальном объекте.
Определения понятия «модель» даны многими авторами [1–5]. В соответствии с [1], математической моделью называется приближенное описание какого-либо класса явлений, выраженное с помощью математической символики.
Имитационное моделирование есть процесс конструирования модели реальной системы с помощью математического и концептуального описания и постановки экспериментов на этой модели при помощи ЭВМ с целью понять поведение, либо оценить (в рамкам ограничений, накладываемых некоторыми критериями или совокупностью критериев) различные стратегии, обеспечивающие функционирование данной системы [3]. Имитационные модели, в отличие от математических, не способны формировать свое собственное аналитические решение, а могут лишь служить в качестве средств для анализа проведения системы в заданных условиях. Поэтому для получения необходимых результатов нужно осуществлять многоразовый «прогон» имитационных моделей, а не решать их.
Таким образом, имитационное моделирование — это есть экспериментальная и прикладная методология, основанная на применении ЭВМ и специального программного обеспечения, целью которой является:
1) описать поведение системы;
2) построить концепцию, объясняющую наблюдаемое поведение;
3) разработать математические зависимости, описывающие отдельные части системы;
4) разработать специальное программное обеспечение;
5) использовать эти разработки для анализа поведения системы при широком изменении факторов.
Среди методов прикладного системного анализа имитационное моделирование является наиболее мощным методом исследования сложных динамических систем, дающим возможность последовательно экспериментировать с системами в случаях, когда делать это на реальных объектах практически возможно или не целесообразно из-за больших материальных или временных затрат.
В настоящей работе было необходимо рассмотреть систему моделей, имитирующих процесс тепло — и массообмена между человеческим телом, подоодежным пространством, одеждой, внешней средой. Целью подобного подхода явилось научное обоснование выбора теплофизических и гигиенических параметров спецодежды.
Впервые тепловая система человека была представлена как система с сосредоточенными параметрами М.Дональдом и Виндхамом в 1950 г. В дальнейшем этот подход был использован при разработке аналоговых моделей терморегуляции человека.
Анализ литературы, посвященной этому вопросу, позволяет разделить существующие математические модели на 3 группы.
К первой группе относятся работы, в которых даны математические модели терморегуляции человека без одежды.
Вторую группу составляют работы, рассматривающие тепловое состояние человека в условиях холода в одежде без обогрева.
К третьей группе следует отнести работы, посвященные описанию математических моделей человека, одетого в теплозащитную одежду с обогревом.
Таким образом, рассматриваемой области предпринимались попытки создания математических моделей тепловых процессов человеческого тела и методик расчета пакетов одежды, основанных на этих моделях. Однако, эти модели относились к области низких температур и очень упрощенно учитывали некоторые компоненты модели. Так, в работе [3] влияние одежды на процесс испарения пота пододежном пространстве учитывается постоянными коэффициентами, в то время, как под одеждой происходят нелинейные процессы тепло — и массопередачи, значительно зависящие от граничных условий. А модель [4], хотя и относится к области повышенных температур, но рассматривает состояние перегрева человека без одежды.
В предлагаемой работе, в отличие от предыдущих, разработаны вопросы процессов тепло и массопередачи в системе «человек –одежда-среда» с учетом явлений, протекающих в пододежном пространстве в жарких климатических условиях и описанных с учетом фундаментальных физических процессов. Такой подход, в противоположность принципу «черного ящика», дает возможность изучать явления при самом широком варьировании внешних воздействий и параметров модели.
Концептуальная модель системы «человек-спецодежда-среда» связана с решением задачи прогнозирования теплового состояния человека и выбора рациональных параметров спецодежды на основе модельных представлений об особенностях теплообмена человека с окружающей средой в жарких климатических условиях.
Решение задачи предполагает поиск параметров спецодежды и ее материалов, удовлетворяющих предъявляемым требованиям, и имеет своей целью определение количественных значений параметров спецодежды с учетом реакций человеческого организма на изменение внешних условий.
Исходная информация включает в себя биологические характеристики человека, параметры пододежного пространства, параметры пакета спецодежды и параметры окружающей среды. Для удобства математического описания система «человек-одежда-среда» представлена многослойным Основной целью является разработка математической модели одежды, работающих в жарких климатических условиях, исследование прочности материала, пропускной способности тепла и ее действие. С этой целью человеческое тело предполагается как деформированное цилиндрическое тело конечного размера, а одежда — мягкая оболочке. Тогда рассматриваемая задача приводится к моделированию деформаций цилиндра с мягким оболочкам.
Исследуется прочность мягкого слоя при воздействии теплового (или механического) воздействия. Данная постановка задачи позволяет исследовать напряженно — деформировано состояние цилиндра при тепловом (или динамическом) воздействии.
Уравнение движения цилиндра с тонкой скрепленной оболочкой при малых движениях принимает следующий вид [1]:
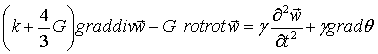 , (1)
, (1)
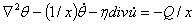 .
.
где 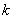 -объемная модуль;
-объемная модуль; 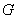 -модуль сдвига;
-модуль сдвига; 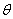 -температура;
-температура; 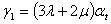 ;
; 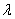 и
и 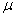 -коэффициенты Ламе;
-коэффициенты Ламе; 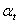 -коэффициент линейного термического расширения;
-коэффициент линейного термического расширения; 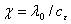 ;
; 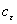 -удельная теплоемкость при постоянной деформации;
-удельная теплоемкость при постоянной деформации; 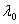 -постоянная величина;
-постоянная величина; 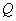 -величина, которой зависит количества тепла;
-величина, которой зависит количества тепла; 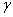 -плотность на единицу объема материала цилиндрического тела;
-плотность на единицу объема материала цилиндрического тела; 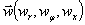 - вектор перемещений цилиндр. На внешний поверхности цилиндра при (
- вектор перемещений цилиндр. На внешний поверхности цилиндра при (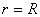 ) ставятся следующие условия [1]:
) ставятся следующие условия [1]:
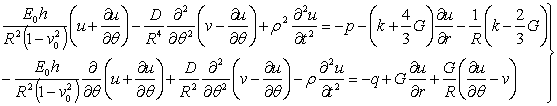 (2)
(2)
Величины 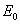 и
и 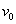 означают соответственно модуль Юнга и коэффициент Пуассона для материала оболочки.
означают соответственно модуль Юнга и коэффициент Пуассона для материала оболочки. 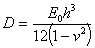 - представляет собой изгибную жесткость оболочки,
- представляет собой изгибную жесткость оболочки, 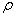 - плотность оболочки на единицу площади средней поверхности. Также к этим уравнениям присоединяем уравнение теплопроводности, описывающее распространение тепловых волн в материале одежды.
- плотность оболочки на единицу площади средней поверхности. Также к этим уравнениям присоединяем уравнение теплопроводности, описывающее распространение тепловых волн в материале одежды.
1) на поверхности (А) одежды задана температура 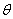 как функция от пространственных координат и времени
как функция от пространственных координат и времени
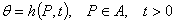 .
.
2) на поверхности (А) одежды задана нормальная компонента градиента температуры как функция координат и времени
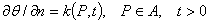 .
.
3) на поверхности одежды (А) задана функция
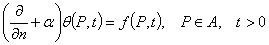 ,
,
где 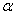 — некоторая константа.
— некоторая константа.
При заданных параметрах 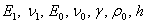 и
и 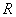 , а также заданных внешних воздействиях
, а также заданных внешних воздействиях 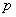 и
и 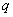 определяются все необходимое неизвестные величины.
определяются все необходимое неизвестные величины.
Решение системы уравнений (1) — (2) в некоторых частных случаях выражается через специальные функции Бесселя первого 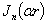 и второго
и второго 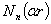 род [2]. Внешние слои цилиндра могут быть многослойными, в этом случае за счет физико- механических параметров системы оптимизируется диссипативные свойств материала одежды. Возможно вместе о системе (1)-(2) применит принцип возможных перемещений [1]:
род [2]. Внешние слои цилиндра могут быть многослойными, в этом случае за счет физико- механических параметров системы оптимизируется диссипативные свойств материала одежды. Возможно вместе о системе (1)-(2) применит принцип возможных перемещений [1]:
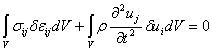 (3)
(3)
где 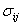 - тензор внутренних напряжений;
- тензор внутренних напряжений; 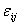 — тензор деформаций;
— тензор деформаций; 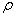 - плотность;
- плотность; 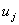 - перемещение точки материала.
- перемещение точки материала.
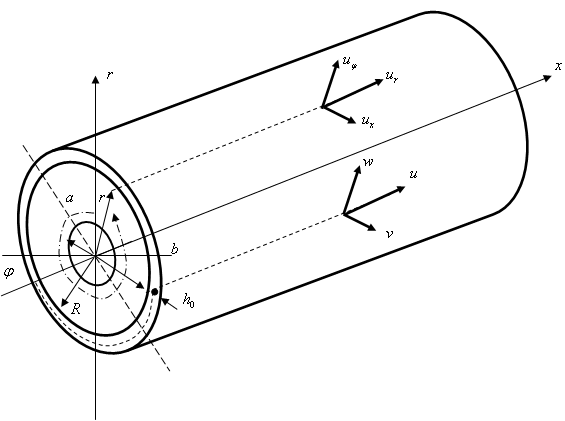
Рис.1. Расчетная схема
Если применить для решения (3) метод конечных элементов, тогда (3) сводится к системе неоднородных алгебраических уравнений высокого порядка:
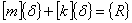 , (4)
, (4)
где 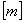 - матрица масс;
- матрица масс; 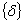 - вектор столбец перемещений;
- вектор столбец перемещений; 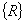 - внешние воздействия. Системы уравнения (4) решается на ЭВМ, с помощью стандартной программы комплекса МАТЛАБ.
- внешние воздействия. Системы уравнения (4) решается на ЭВМ, с помощью стандартной программы комплекса МАТЛАБ.
Математическая модель системы «человек -одежда -среда» (1) –(4) представляет собой систему дифференциальных уравнений, описывающих процесс теплообмена человека, процессы тепло — и массообмена в пододежном пространстве, процессы тепло- и влагопереноса в пакете одежды и процессы тепло- и массообмена поверхности одежды с окружающий средой в жарких климатических условиях.
Параметры и коэффициенты системы «человек -одежда -среда» соответствуют показателю среднего условного человека с весом 71 кг, площадью поверхности тела 1,65 м2 теплопродукцией 85 Вт, энергозатратами 234 Вт; показатели окружающей среды: температура воздуха 25–450С, относительная влажность 40 % [2,3].
Изложенная концептуальная модель системы «человек -одежда -среда» дает возможность на основе применения математических методов исследования определить условия физических экспериментов с дальнейшим уточнением и оптимизацией основных параметров, а также количественно оценить эффективность выбора материалов и конструкции одежды на этапе проектирования.
Литература:
1. В.Новацкий. Динамические задачи термоупругости. Издательство «Мир» Москва 1970, 256 с.
2. Жаворонков А. И. Математическая модель системы «человек -теплозащитная одежда -среда» с АСР температуры В сб.: Автоматизация технологических процессов легкой промышленности, М., 1982.
3. Gagge A. P. A model of temperature regulation in man. Ted. Proc., 1973, v.32.







