В статье рассматривается решение задачи оптимального распределения ресурсов в процессе выполнения административных регламентов с целью повышения их выполнимости при помощи модифицированного генетического алгоритма.
Ключевые слова: административный регламент, генетический алгоритм, распределение ресурсов.
Главное назначение административных регламентов (АР) заключается в интеграции в единое функциональное целое совокупности процессов и операций, реализуемых субъектами действия над существующими объектами в интересах, определенных нормативными регуляторами и инструкциями, для достижения заданной цели [1]. Поэтому если рассматривать АР как алгоритмический процесс, реализующий государственную услугу, то его основу будут составлять процессы и операции, закрепленные в нормативно-правовом акте АР (см. рис.1). Типовая структура АР предполагает наличие описания административных процедур c, каждая из которых достигается путем выполнения определенной последовательности задач z:
где P — предикат наличия элемента системы (P(e) — принимает значение «истина», если e существует в системе),
k >0.
При этом сам АР R будет характеризоваться последовательностью процедур:
где k >0.
Каждая задача предполагает совершение определенных операций субъектов над объектами, то есть:
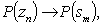
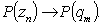
Субъект-пользователь инициирует выполнение первой задачи последовательности, в результате чего запускается процесс выполнения АР. При этом субъекты и объекты выступают в качестве ресурсов, необходимых для перехода от одной задачи к другой [2].
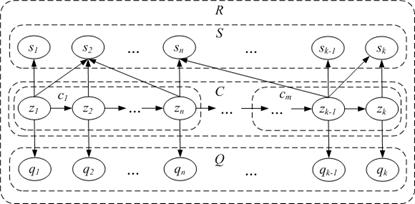
Рис. 1. Типовая структура административного регламента
Основные проблемы, препятствующие выполнению требований АР можно разделить на две группы:
- связанные с логической противоречивостью описания процессов АР;
- возникающие в процессе выполнения АР.
Решение проблем логической противоречивости связано с правильным выбором методов и средств моделирования информационных процессов, подходящих для описания АР. Построение адекватной информационной модели АР позволит выявить противоречия в описании до его реализации виде совокупности информационных процессов, исключая появление в системе ряда угроз функциональной безопасности. Однако проблемы, возникающие в процессе выполнения, являются следствием отсутствия либо неправильного распределения ресурсов системы — субъектов и объектов и требуют решения оптимизационных задач. Решение одной из таких задач предлагается авторами данной статьи.
Как уже было отмечено ранее, выполнение некоторой задачи zn связано с наличием в системе соответствующего субъекта sm' и объекта qk', которые можно определить как необходимые требования для zn. Однако стоит отметить, что система государственного управления является динамичной системой и поэтому соблюдение условий P(sm')→P(sm) и P(qk')→P(qk) зависит от того, заняты ли sm и qk вмомент времени ti, где ti — время начала выполнения задачи zn:
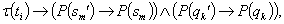
где t(ti) — предикат, принимающий значение «истина»
в момент времени ti.
При этом как показывает практика, каждый объект АР уникален и соответствует только одной задаче. Поэтому решение задачи обеспечения выполнимости АР состоит в согласовании множества необходимых объектов Q' и существующих в системе Q:
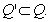
Иная ситуация обстоит с субъектами. Каждый субъект в системе государственного управления функционально может выполнять несколько задач АР. Поэтому для обеспечения выполнимости АР необходимо решение оптимизационной задачи, направленной на эффективное распределение задач между субъектами-исполнителями.
Рассмотрим процедуру решения задачи оптимального распределения субъектов-исполнителей, входящих в группу So(с общим количеством субъектов-исполнителей a), где каждый из субъектов-исполнителей snÎSo функционально может быть задействован в выполнении задач из группы Zl(с общим количеством задач b). Учитывая, что процесс выполнения задач непрерывный, а процесс поступления задач на выполнение случайный, то АР можно рассматривать как сеть узлов массового обслуживания, где каждый узел — это субъект-исполнитель sn, который представляет собой систему массового обслуживания, выполняющую поток заявок lk, соответствующий задаче zkÎZl. Учитывая, что интервал между заявками и длительность выполнения задач распределены по законам A(t) и B(t), которые необходимо определять отдельно для каждого случая (отдельно для каждого исполнителя и АР в целом) и которые также могут изменяться во времени, то следует воспользоваться общим решением для одноканальных систем массового обслуживания G/G/1, которое характеризует выполнение некоторого потока задачи zk (или задач zk,…,zk+p) исполнителем sn. На основании решений для системы G/G/1 можно определить, сколько будет выполняться задача при заданных параметрах системы, которыми являются:
- среднее фактическое время выполнения задачи tZk;
- средняя интенсивность поступающих заявок lk;
- среднеквадратическое отклонение значения интервала между поступающими заявками sA;
- среднеквадратическое отклонение значения длительности выполнения задач sB.
Рассмотрим математическую модель контроля основных параметров, влияющих на выполнимость на основе ТМО. Анализ многочисленных результатов (например результатов работ [3–5]) показывает, что наиболее удачное приближение для расчета среднего времени пребывания заявки для системы G/G/1 дает формула
, (1)
где , ,
Величины ls иts определяются следующим образом:
ls — суммарный поток заявок для исполнителя s, который равен
, где lk,…,lk+p — интенсивности поступления заявок на выполнение всех задач, выполняемых субъектом s;
ts — среднее время выполнения задач субъектом s, которое определяется как
, (2)
где
Для определения коэффициента вариации интервала между поступающими заявками vAs воспользуемся уравнением средней дисперсии для мультиплексированного входящего потока системы G/G/1, приведенным в работе [6]:
. (3)
Коэффициент вариации интервала между поступающими заявками в свою очередь будет равен
, (4)
Для определения коэффициента вариации длительности выполнения задач vBs необходимо учитывать, что субъект sn выполняет задачи последовательно, поэтому нужно рассматривать множество значений длительности выполнения задач как совокупность с математическим ожиданием ts, состоящей из групп с параметрами tk,…,tk+p и sBk,…,sBk+p. Воспользоваться правилом сложения дисперсий получим общую дисперсию длительности выполнения для sn
. (5)
Отсюда коэффициент вариации по определению равен
.
В случае если одну задачу (один поток) выполняет несколько субъектов, то необходимо воспользоваться решением для параллельных каналов с различным временем облуживания [7], то есть поступающее требование направляется на один из каналов (к одному из исполнителей) с вероятностью:
. (6)
Поэтому поток заявок для каждого из исполнителей задачи zk будет равен:
. (7)
Таким образом, выражение 2 позволяет оценить среднее время пребывания заявки у исполнителя sn. Однако использовать данное значение для оценки выполнимости АР не возможно, так оно является общим для всех задач, выполняемых исполнителем s. Поэтому необходимо определить среднее время обслуживание для каждой задачи zk,…,zk+p, выполняемой sn — Tk,...,Tk+p. Для этого рассмотрим следующую модель.
Рассмотрим узел СМО (отдельного исполнителя) как многоканальную систему (см. рисунок 2), где каждая заявка перед обслуживанием попадает в бесконечный накопитель Н, а каждый канал КN связан с выполнением определенной задачи из множества zk,…,zk+p.
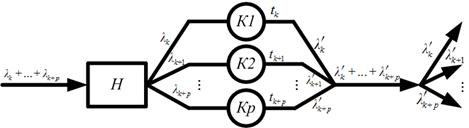
Рис. 2. Модель системы обслуживания потока различных задач АР
Учитывая, что накопитель Н является общим для всех потоков lk,…,lk+p, то среднее время ожидания в очереди будет одинаковым для всех заявок zk,…,zk+p. Поэтому с учетом 2 время пребывания заявки в системе для каждой из задач, выполняемых исполнителем sn будет определяться по формуле
. (8)
Просчитав для каждой задачи среднее время выполнения Ti и сравнив их с максимальным временем Timax, определенным нормативными регуляторами АР, можно сказать, что если Ti > Timax, то задача не выполняется с заданными условиями. Результат представим в виде коэффициента:
. (9)
В том случае, если задачу zi выполняет несколько исполнителей sn,…,sn+l, то для сравнения выбирается максимальное значение времени пребывания заявки в системе:
. (10)
Показатель ak характеризует загруженность субъекта-исполнителя при выполнении задачи zk и позволяет оценить запас времени, который доступен для решения других задач из группы Zl.
Решение любых задач распределения ресурсов требуют выбора определенного критерия в качестве целевой функции, на получение оптимальных значений которого и будет направлена задача.
Как уже было отмечено в первой главе, в качестве целевой функции необходимо использовать показатель, который характеризует насколько сбалансировано распределение исполнителей между задачами АР. В качестве такого показателя целесообразно использовать дисперсию величины ak каждой из задач АР:
. (11)
Теперь рассмотрим процедуру распределения задач между субъектами-исполнителями. Приведем технологическую матрицу, характеризующую распределение ресурсов в системе. В левом столбце приведены все задачи группы Zl, в верхней строке все субъекты группы So.
Таблица 1
Матрица распределения ресурсов в системе
|
Z |
S |
|||||
|
s1 |
s2 |
… |
sn |
… |
sa |
|
|
z1l1, sA1, T1max |
x11 |
x21 |
… |
xn1 |
… |
xa1 |
|
z2l2, sA2, T2max |
x12 |
x22 |
… |
xn2 |
… |
xa2 |
|
… |
… |
… |
… |
… |
… |
… |
|
zk lk, sAk, Tkmax |
x1k |
x2k |
… |
xnk |
… |
xak |
|
… |
… |
… |
… |
… |
… |
|
|
zblb, sAb,Tbmax |
x1b |
x2b |
… |
xnb |
… |
xab |
Для каждой задачи также указывается поток заявок lk и среднее время выполнения tZnk. При этом сумма каждой строки должна быть больше 0, так как для любой из задач должен быть определен исполнитель:
(12)
Таким образом, задача распределения ресурсов схожа с классической задачей распределения ресурсов в транспортной сети (между поставщиками и потребителями, мощностей между каналами передачи данных и т. п.) и состоит в определении величин xnk — поставка n-субъекта k-задаче, которая может принимать значение 1 либо 0. При этом для каждой из задач выполняется условие ak≤ 1, а величина D(a) минимальна.
В работе [8] проведен подробный анализ методов оптимизации для решения задачи подбора технических средств охраны. Рассматриваемая в работе задача, также как и решаемая авторами данной статьи, имеет множество дискретных решений и сложную целевую функцию и также относится к NP-полным, в связи с чем был выбран генетический алгоритм. Поэтому целесообразно применить этот метод для решения поставленной задачи.
Теперь рассмотрим каждый из этапов решения задачи с помощью классического генетического алгоритма (разработанным Холландом [9]). Вначале случайным образом выбираются N(N≥b) значений вектора x (начальная популяция изNособей), каждое из которых соответствует системе неравенств 12 и условию ak ≤ 1. Далее генерируется промежуточная популяция — это набор особей, получивших право размножаться. Для генерации промежуточной популяции используется принцип пропорционального отбора, заключающийся в том, что каждая особь попадает в популяцию с вероятностью, пропорциональной ее приспособленности. Для данной задачи: чем меньше значение D(a), тем больше вероятность попадания в промежуточную популяцию:
(13)
Далее особи в случайном порядке разбиваются на пары, и производится скрещивание (обмен случайными отсеченными частями):
К полученному в результате отбора и скрещивания новому поколению применяется оператор мутации, который инвертирует каждый бит популяции с вероятностью 1/N. Далее из полученных особей выбираются только те, что соответствуют системе неравенств 12 и условию ak<1, после чего цикл повторяется снова. Процесс эволюции (цикл отбор-скрещивание-мутация) может продолжаться бесконечное число шагов, поэтому критерием останова является получение сходимости целевой функции за n число шагов, либо достижения максимального количества итераций. При этом оптимальному значению вектора x будет соответствовать наиболее приспособленная особь из последнего поколения:
(14)
Блок-схема классического генетического алгоритма приведена на рисунке 3.
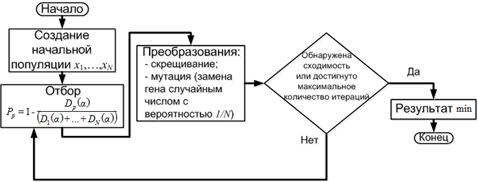
Рис. 3. Классический генетический алгоритм
Исследование полученного генетического алгоритма, выполненного в среде MATLAB, для распределения 26 задач между 8 исполнителями показывают, что он уступает алгоритму General Pattern Search (GPS), представляющий собой разновидность симплексного метода, входящей в пакет MATLAB (см. рисунок 4).
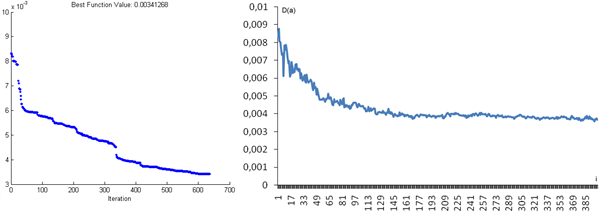
Рис. 4. Процесс оптимизации целевой функции при помощи алгоритма GPS (слева) и классического генетического алгоритма (справа)
Использование алгоритма GPS дает возможность получить наименьшее значение целевой функции (D(a)=0,00341268) за одно и то же время работы (2 часа), как и классический генетический алгоритм (D(a)=0,003580429). Поэтому автором данной статьи предлагается ряд модификаций, позволяющих улучшить сходимость генетического алгоритма. Блок-схема модифицированного генетического алгоритма приведена на рисунке 5.
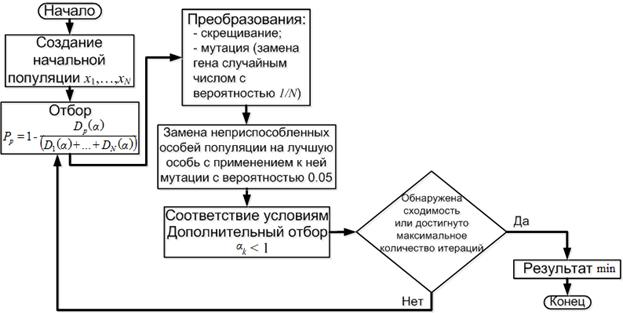
Рис. 5. Модифицированный генетический алгоритм
В данном генетическом алгоритме улучшение сходимости достигается путем дополнительного преобразования полученной после скрещивания и мутации популяции, которое включает в себя замену неприспособленных особей на лучшую особь с применением к ней мутации и вероятностью 0,05. После этого выполняется дополнительный отбор, который исключает особей, не соответствующих условию ak ≤ 1.
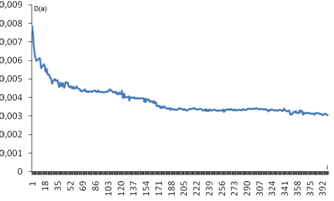
Рис. 6. Процесс оптимизации целевой функции при помощи модифицированного генетического алгоритма
Результаты вычислительного эксперимента показали, что введенные модификации позволили получить лучшее значение целевой функции (D(a)=0,003037381) при одинаковом количестве итераций (400) и времени работы алгоритма. Поэтому полученный модифицированный генетический алгоритм может быть использован в практических целях для решения задачи повышения выполнимости АР.
Литература:
1. Региональное электронное правительство: стратегия создания, архитектура, типовые решения / Под ред. В. И. Дрожжинова, А. А. Лучина. — М.: Эко-Трендз, 2004. — 288 с.
2. Копытов В. В., Науменко В. В., Минин В. А., Зайцев А. А. Анализ проблем обеспечения бесконфликтного выполнения электронных административных регламентов // Сборник научных статей (выпуск XII) / Ставропольский филиал ИГУТИ. — Ставрополь, 2012 — С. 72–78.
3. Шнепс М. А. Системы распределения информации. Методы расчета.- М.:Связь, 1979.-344 с.
4. Алиев Т. И. Основы моделирования дискретных систем. — СПб: СПбГУ ИТМО, 2009. — 363 с.
5. Нгуен Дык Тай Методы и средства исследования распределенных сетей передачи данных с неоднородным трафиком на основе неэкспоненциальных моделей: дис. канд. техн. наук: 05.13.13 / Нгуен Дык Тай. — М., 2009. — 145 с.
6. Бахарева, Н. Ф. Аппроксимативные методы и модели массового обслуживания для исследования компьютерных сетей: дис. д-р техн. наук: 05.13.15 / Н. Ф. Бахарева. — Пенза, 2011. — 335 с.
7. Саати, Т. Л. Элементы теории массового обслуживания и её приложения / Т. Л. Саати. — М.: Советское радио, 1971. — 520 с.
8. Давидюк Н. В. Разработка системы поддержки принятия решений для обеспечения физической безопасности объектов [электронный ресурс]: дис. канд. техн. наук: 05.13.01, 05.13.19 — Астрахань: РГБ, 2010.
9. Holland J. H. Adaptation in Natural and Artificial Systems: an Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence / J. H. Holland. — Massachusetts Institute of Technology, 1992. — 328 p.







