Ключевые слова: Топология, лист (лента) Мёбиуса.

Как специалисту железнодорожного транспорта, так и специалисту в любой другой отрасли необходимо развивать такие качества, как самообразование, расширение кругозора, наблюдательность, умение понимать процессы с точки зрения математики. Для развития пространственного воображения помогает такой раздел математики, как топология. Топология — часть математики, изучающая в самом общем виде явление непрерывности пространства и плоскости [1,2,3].
Топология не входит в учебную программу математики СПО, но на мой взгляд представляет большой интерес. Поэтому решил расширить знания по математики и поделиться ими со студентами (проводя анкетирование, опыты и открытые уроки). А также стал интересен взгляд прохожих людей в городе Саратове (как молодежи, так и людей в возрасте) на данный раздел математики Топология и имеют ли понятия люди, не зависимо от возраста человека, о листе Мёбиуса и его свойствах.
Целью в проекте поставил применение математического моделирования в науке и технике на основе исследования свойств листа (ленты Мёбиуса).
Для решения поставленной цели рассмотрел ряд задач:
- Изучить основные понятия и теоремы раздела «Топология».
- Ознакомиться с биографией Мёбиуса и его научными работами.
- Систематизировать информацию о листе Мебиуса и его свойствах.
- Собрать информацию о применении свойств листа Мебиуса в науке и технике.
- Провести опыты с лентой Мёбиуса.
- Провести анкетирование на знание студентов в области топологии, в частности листа Мёбиуса.
- Рассмотреть перспективы применения ленты Мёбиуса на железнодорожном транспорте.
Объектом исследования выбрал лист Мёбиуса, как элемент топологии, ярко демонстрирующий его основные свойства.
Методы исследования выбрал: научная абстракция, метод факторного анализа, синтеза, прогнозирования.
Тема «Исследование листа мёбиуса с точки зрения математики» актуальна в наше время, так как именно на листе Мёбиуса можно наблюдать проявление таких свойств, как связность, односторонность, непрерывность, неориентированность, а также хроматическое число, которое равно шести.
Основоположником односторонней поверхности является Август Фердинанд Мёбиус (1790–1868) — немецкий математик, астроном, геометр. Он ученик Гаусса и Пфаффа, а также внес в развитие математики много идей, что принесло ему известность в научном мире. Возможно, увлеченность астрономией и математикой привело его к теории топологии, в частности появлению листа (ленты) Мёбиуса.
Лист Мёбиуса — топологический объект, простейшая односторонняя неориентируемая поверхность, которая имеет всего лишь один край (см. Рис.1.). Ведь попасть из одной точки этой поверхности в любую другую можно, не пересекая края [4].

Рис. 1. Лист (лента) Мёбиуса
Все эти перечисленные свойства Мёбиуса используются в жизни человека. Только в разных сферах, например, в технике, литературе, вязании и во многом другом. В проекте будет много описано, где применяются свойства этого листа, так как мало кто знает (а это показало анкетирование).
В наше время модны снуды (шарфы, но сшитые по-другому принципу), которые можно носить как объемный воротник если намотать его, или как воротник — хомутик, а также можно надевать как жилет. А лента Мёбиуса это тот же снуд, только перевернутый.
В виде парадоксальной геометрической фигуры изготавливаются также лопасти обычного бытового миксера.
Полоса ленточного конвейера выполняется в виде ленты Мёбиуса, что позволяет ему работать дольше, потому, что вся поверхность ленты изнашивается равномерно.
В большинстве матричных принтеров, внутри находящееся красящее устройство также имеет вид листа (ленты) Мёбиуса для увеличения его ресурса (см. Рис. 2).

Рис. 2. Матричный принтер
В 1923 году выдан патент изобретателю Ли де Форсу, ведь именно он предложил записывать звук на киноленте без смены катушек, следовательно, сразу с двух сторон (см. Рис. 3).

Рис. 3. Кинолента
Имеются воплощения этого листа Мёбиуса в строительстве. Построенны в Англии (в Лондоне) велодром имеет контуры, которые можно назвать вариацией на тему листа Мёбиуса.
Аттракцион «Американские горки» необыкновенны тем, что они и похожи в большой степени на ленту Мёбиуса и имеют такой вид, что у многих людей, посещавших эти горки, приводили в восторг не только от быстроты езды, но и как раз от красоты.
В настоящее время рассматривается проект постройки библиотеки, который будет выполняться в виде ленты Мёбиуса в Казахстане.
Невероятно, даже Международный символ переработки представляет собой Лист Мёбиуса.
Лист Мёбиуса считают символом современной математики, так как именно он дал толчок новым математическим исследованиям, ведь свойства листа Мёбиуса удивительны.
В наше время пока действуют нынешние правила дорожного движения, без светофоров нам не обойтись. Поэтому дизайнеры предлагают все новые и новые, все более и более наилучшие модели этих устройств. Впрочем, здесь главное — не переусердствовать: авторы некоторых уже известных нам концептуальных светофоров явно пожертвовали простотой и понятностью в угоду эффективности. А вот светофор в виде ленты Мёбиуса очень прост, аккуратен, но в тоже время функционален. Здесь есть отдельное большое световое табло для пешеходов и отдельное — для водителей. На каждом из них ведется обратный отсчет времени. А, кроме того, светофор служит одновременно и уличным фонарем (см. Рис. 4).

Рис.4. Светофор в виде ленты Мёбиуса
И во многом, многом другом применяются свойства необыкновенного листа.
Ранее говорилось о проявлениях свойств в данном листе и его необычности. Если рассуждать, теоретически, то с лентой Мёбиуса можно производить немалое количество комбинаций.
Если обычную ленту разрезать вдоль по линии, равноудалённой от краёв, вместо двух лент Мёбиуса получится одна длинная двухсторонняя (в два раза больше закручена оборотов, чем сама лента Мёбиуса) лента, которую называют в наше время «Афганская лента».
Если теперь эту ленту разрезать вдоль посередине, то получаются уже две ленты, намотанные друг на друга.
Если разрезать ленту Мёбиуса, отступая от края примерно на треть или четверть её ширины, то получаются две ленты, одна — более короткая лента Мёбиуса, другая — длинная лента с двумя полуоборотами, а это значит, что получается снова «Афганская лента».
Если разрезать ленту с тремя полуоборотами, то получится лента, завитая в узел трилистника.
Свойства листа Мёбиуса с теоретической точки зрения:
Односторонность
Первое заметное свойство в листе (ленте) было: односторонность, а именно, лист Мёбиуса имеет одну сторону, а значит и одну грань.
Непрерывность
На листе Мёбиуса любая точка может быть соединена с любой другой точкой, так как разрывов нет, а значит непрерывность полная.
Связность.
Если квадрат разрезать от стороны к стороне, то он распадётся на два отдельных куска (части). Точно также если разрезать яблоко на две части, но вот чтобы располовинить кольцо, нужно уже два разреза. И два раза придётся резать бублик, а вот уже, например, телефонный диск можно десять раз рассечь ножом от одной замкнутой кривой до другой, а он останется единым целым. Поэтому любой тополог скажет, что квадрат и ромашка — односвязны, кольцо и оправа от очков — двусвязны, а всяческие решётки, диски с отверстиями и подобные сложные фигуры — многосвязны.
На основе данных примеров можно сказать, что лист Мёбиуса также двусвязен, так как при разрезании его вдоль, получим не два кольца, а одну ленту.
Хроматическое число № 6
Хроматическое число — это максимальное число областей можно поделить поверхность так, что каждая будет иметь общую границу со всеми другими. Если по-разному выкрасить эти области, то любой цвет должен соседствовать со всеми остальными [5].
Хроматическое число, например:
Плоского листа, цилиндра, сферы = 4.
У тора = 7.
Листа Мёбиуса = 6.
Все эти свойства показывают, что этот лист и вправду необыкновенный!
Для подтверждения всех комбинаций и свойствах листа Мёбиуса решил практически совершить ряд опытов и продемонстрировать их студентам для расширения своего кругозора и развития логического мышления.
Опыт № 1(проверка свойства — односторонность)
В наше время мы привыкли встречаться с двусторонними предметами (объектами, фигурами). Изучив свойства ленты Мёбиуса и узнав, чтобы она односторонняя решил это проверить. Закрасил одну сторону ленты Мёбиуса.

Рис. 5. Одна закрашенная сторона ленты
Результат:
Лист Мёбиуса закрасился полностью, а это значит, поверхность листа Мёбиуса односторонняя.
Из книги «Что такое математика?» Рихард Курант и Герберт Робинс пишут:
«Если кто-нибудь вздумает раскрасить только одну сторону поверхности мёбиусовой ленты, пусть сразу погрузит её всю в ведро с краской»
Если разукрасить две стороны ленты (см. Рис. 5 и см. Рис. 6) и склеить, повернув на 1800 одну сторону ленту, то и будет первоначальное изображение ленты Мёбиуса (см. Рис. 7).

Рис. 6. Две закрашенные стороны ленты

Рис. 7. Лента Мёбиуса
Провел опыты как с обычным кольцом (листом бумаги), так и кольцом Мёбиуса, а также исследовал свойства листа Мёбиуса и его отличительные характеристики по сравнению с обычным в опытах № 2,3,4.
Опыт № 2 (проверка свойства — непрерывность).
Сделал изначально обычное кольцо и кольцо Мёбиуса. Нарисовал символ на одной стороне каждого кольца и начертил непрерывную линию посередине, начиная с символа, пока не вернется в первоначальное место.
Результаты:
Обычное кольцо
Линия проходит вдоль кольца по одной стороне, сходясь в символе (точке). Вторая сторона остается такая же, какая и была. А это значит, что свойства непрерывности в обычном кольце не наблюдается (см. Рис. 8).

Рис. 8. Обычное кольцо
Кольцо Мёбиуса
Непрерывная линия проходит по двум сторонам, заканчиваясь в начальном символе (точке). А это значит, что поверхность листа Мёбиуса является непрерывной (см. Рис. 9).

Рис. 9. Кольцо Мёбиуса
Опыт № 3 (проверка на количество краёв в листе Мёбиуса)
Закрасил непрерывной линией только один край колец как обычного кольца, так и кольца Мёбиуса.
Результаты:
Обычное кольцо
Один край кольца был закрашен, а второй край нет. Значит, имеет два края, так как второй остался чистым.
Кольцо Мёбиуса
Линия края получилась, оказалась закрашена вся. Следовательно, лист Мёбиуса имеет один край
ЭТО УДИВИТЕЛЬНО: Лист Мёбиуса действительно непрерывен, односторонен и имеет один край.
Опыт № 4 (что же произойдет, если разрезать обычное кольцо и кольцо Мёбиуса?).
Разрезал данные кольца посередине, получил:
Результаты
Обычное кольцо
Получилось 2 кольца с одинаковой длиной и шириной (ширина будет одинакова, только если разрезать пополам, а длина всегда остается неизменной).
Кольцо Мёбиуса
Получилось одно перекрученное кольцо, но уже в виде восьмёрки (или бесконечности), причем длина которого в два раза больше, а ширина в два раза уже (см. Рис. 10).

Рис. 10. Разрезанный лист Мёбиуса
Опыт № 5 (Что же произойдет, если разрезать разрезанный лист (ленту) Мёбиуса?)
Порезал данную, получившуюся ленту Мёбиуса на две равные части, получил:
Результат
Два сцепленных друг с другом кольца, тем самым очередной раз подтвердил свойство непрерывности (см. Рис. 11).

Рис. 11. Двух кратное разрезание листа Мёбиуса
В анкетировании приняло участие 110 студентов, обработав анкету, получил следующие результаты:
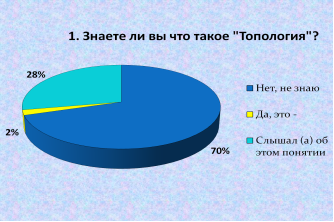
1. Знаете ли вы что такое «Топология»? — ответили:
Нет, не знаю — 77 человек = 70 %.
Да, это — 2 человека = 2 %.
Слышал (а) об этом понятии — 31 человек = 28 %.
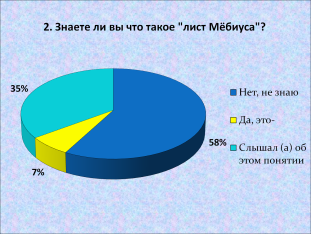
2. Знаете ли вы что такое «лист Мёбиуса»?– ответили:
Нет, не знаю — 64 человека = 58 %.
Да, это — 8 человек = 7 %.
Слышал (а) об этом понятии — 38 человек = 35 %.
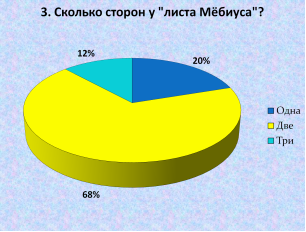
3. Сколько сторон у «листа Мёбиуса»?–ответили:
Одна — 22 человека = 20 %.
Две — 75 человек = 68 %.
Три –13 человек = 12 %.
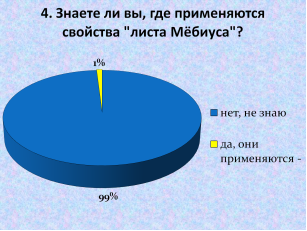
4. Знаете ли вы, где применяются свойства «листа Мёбиуса»? — ответили:
Нет, не знаю — 109 человек = 99 %.
Да, они применяются — 1 человек = 1 %.
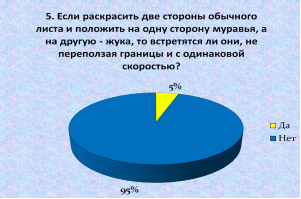
5. Если раскрасить две стороны обычного листа и положить на одну сторону муравья, а на другую — жука, то встретятся ли они, не переползая границы и с одинаковой скоростью? — ответили:
Да — 5 человек = 5 %.
Нет — 105 человек = 95 %.
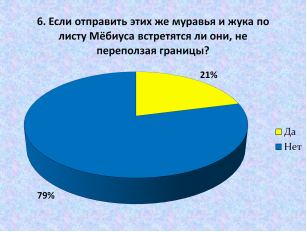
6. Если отправить этих же муравья и жука только по листу Мебиуса встретятся ли они, не переползая границы и с одинаковой скоростью? — ответили:
Да — 23 человека = 21 %.
Нет — 87 человек =79 %.
Из анкетирования видно, что большинству опрошенных не знаком лист Мёбиуса, а это подтверждает, что тема актуальна. Ведь простой лист, с одной стороны перевернутый на 180 градусов, несет в себе множество свойств, таин, а самое главное многозначное применение. А, студенты, увидев вопрос: «Где применяются свойства листа Мёбиуса» ответило всего 1 % опрошенных, а это говорит о том, что никто не знает ответ на поставленный вопрос. И моей, после анкетирования, целью стало расширить знание студентов о листе Мёбиуса.
На знании свойств ленты Мёбиуса решил внести свой небольшой вклад в развитие железной дороги, а именно гипотезу применения листа Мёбиуса на железнодорожном транспорте. Стандартизация в мире абсолютно одинакова с точки зрения математики, а предположение, которое, возможно, останется «следом» в науке отличатся как в архитектурно — художественном плане, так и в экономичном. На рис. 12. изображена тележка вагона со стандартной боковой рамы.

Рис. 12. Стандартный вид боковой рамы тележки вагона
На общем рис. 13, а именно рисунке № 1 показал схематичное изображение боковой рамы в тележке. При создании этой боковой рамы сплав применять такой же, но более твердую часть сплавить на верхнем поясе, ведь именно там состоится небольшой перегиб для перехода из одной стороны в другую. На рисунке № 2 показал то, что можно также поместить для безопасности внутренних устройств по краям тележки дверки, которые четко закрепляются между собой металлическим крючком и маленькой впадиной. При их закрывании безопасны все внутренние устройства, например, от попадания пыли внутрь к пружинам, а если быть точнее в их проемы. Из этого следует, что и боковая рама защищена повышенной тягой. На рисунке № 3 расположена сама тележка с изменением вида боковой рамы, при которой показал штриховыми линиями, что она похожа на ленту Мёбиуса и обладает этими же свойствами — односторонность, неориентированность и другие. Но в данном случае особую роль играет свойство непрерывности
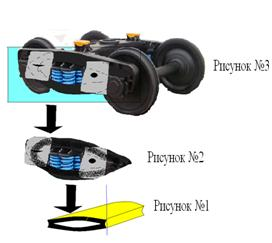
Рис. 13. Схематичное изображение трех в совокупности рисунков боковой рамы тележки вагона, выполненных в виде ленты Мёбиуса
Рассматривая отдельные составные элементы боковой рамы, как показано на Рис. 14, то можно сказать, что вся верхняя часть будет считаться обрезной (то есть срезаться непосредственно до краёв верхнего пояса), а это значит меньше количества материала для изготовления этой рамы. Из этого следует, что одним из преимуществ будет считаться экономия бюджета.
Рассмотрел достоинства и недостатки данной модели:
Достоинства
- Повышена безопасность внутренних пружин.
- Увеличена эффективность на осевую нагрузку боковой рамы, так как на верхнем поясе состоялся перегиб.
- По скорости изготовления боковая рама будет изготовлена быстрее, так как будет происходить сплав по одну сторону, а не по две.
- Улучшена часть верхнего пояса боковой рамы.
- Имеет особый вид (в виде ленты Мёбиуса), тем самым отличается от других боковых рам.

Рис. 14. Составные элементы боковой рамы тележки вагона
Недостатки
- Увеличилось количество деталей (дверок), тем самым увеличивается вес боковой рамы.
- Не для всех видов вагонов может применяться эта боковая рама. Но вполне реально может применяться для полувагонов, крытых вагонов и платформ.
- Может возникнуть проблема при сплаве верхнего пояса боковой рамы.
В заключение можно, что полностью подтвердил свойства непрерывности, односторонности, неориентируемости листа Мёбиуса. Самое главное для меня в этом проекте это формирование умения познавать новое, планировать свою работу и осуществлять её, что необходимо будущему специалисту конкурентно-способным на рынке труда. Получая знания сам — поделись с другими! Поэтому первоначально я выяснил осведомленность моих сокурсников в данной теме, проведя анкетирование, которое показало, что 58 % не знают, что такое лист Мёбиуса; 70 % не знают, что такое топология и чем она занимается; 99 % даже не имеют представления о практическом применении листа Мёбиуса. Вследствие этого я решил, что мой проект актуален для моих сверстников и провел вышеизложенную работу.
В ходе работы над проектом проанализировал и систематизировал информацию по применению листа Мёбиуса. Для этого проводил открытые уроки со своими сокурсниками и повышал не только свой кругозор, но их. А свойства этого листа применяются в архитектуре, живописи, поэзии, техники и во многом другом, а, как показало анкетирование, этого никто не знал и не мог себе даже предположить, что такое применение существует в нашем мире.
Эх, Мёбиус, ты создал чудо!
Простой всего лишь лист в пол оборота,
Он подарил красоту и необычность.
Здесь нет пределов и нет ограничений!
(Ерохин М. А «Необыкновенный лист Мёбиуса»)
Литература:
1. Большая советская энциклопедия. Главный редактор Б. А. Введенский. Второе издание. Сведения о Топологии и топологических объектов.
2. Математическая энциклопедия. Главный редактор И. М. Виноградов. Сведения о Топологии и топологических объектов.
3. Элементарная топология. О. Я. Виро, О. А. Иванов, Н. Ю. Нецветаев, В. М. Харламов
4. Большая советская энциклопедия. Главный редактор Б. А. Введенский. Второе издание. Сведения о листе Мёбиуса.
5. Математическая энциклопедия. Главный редактор И. М. Виноградов. Сведения о листе Мёбиуса.







