Несмотря на то что, построения трисекции угла при помощи линейки и циркуля является древнейшей задачей геометрии, еще она не потеряла своей актуальности для энтузиастов науки.
Наши исследовании по этому вопросу показали [2], что у некоторого угла Фалеса существует следующее легко доказуемое свойство угла, которого мы называли «свойством Темура»: «Заключенные отрезки пучка параллельных прямых между сторонами угла имеют общий разделитель. Длина которого равно длине первой прямой от вершин угла или разности длин соседних отрезков».
Если представить, что вместо пучка параллельных прямых, будут концентрические дуги или окружности с бесконечно большими радиусами, то вышеприведенное свойство можно применить и к углу или окружности.
Действительно так. Длина дуги и окружности прямо пропорционально их радиусу. То есть, если их радиус увеличить или уменьшить на одну единицу отрезка, то и длина дуги или окружности так же увеличиться или уменьшится на одну единицу, равную длине первой прямой или дуги от вершин угла, рис.1. Из рисунка видно, что длина первой прямой или дуги от вершин угла, делить второй прямой или дуги на две равные части, третей прямой или дуги на три равные части и и. т.
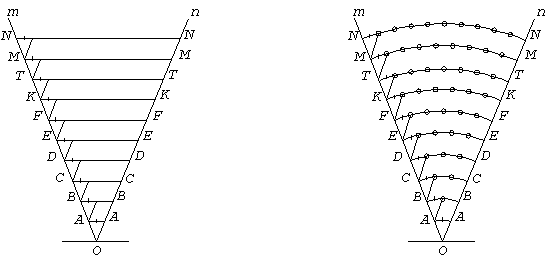
Рис.1
Наши исследования показали, что используя эти свойства можно с высокой точности построить трисекцию угла. Например, дан некоторый угол α, рис. 2. Из свойства Темура следует, длина первой дуги радиусом R, разделит дугу окружности радиусом 3R на равные три части
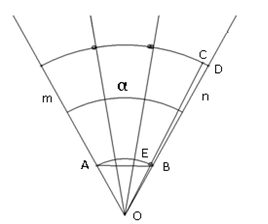
Рис. 2.
Пусть дан некоторий угол α. На основани выше преведенного свойства угла разработали следующий способ построения трисекции угла:
1. При помощи циркуля проводим дугу радиусом R1=10 мм и R3=30 мм опирающие к сторонам m и n угла α, рис.2;
2. На основании свойства Темура длина первой дуги делит вторую на равные три части. Обычно в практике, в место длины дуги пользуются длиной хорды уперающей концам дуги, которая всегда меньше чем длина дуги. И именно по этому, построения трисекции угла остаётся абсалютно точно не решенной задачей геометрии.
И по этому в нашем случае, когда хорды АВ первой дуги откладываются три раза по дуге второй, то всегда остаётся остаток дуги СD. Если СОD представить как некоторий малый угол, то хорда ЕВ приближонно делит СD на три равные части.
3. От первой точки дуги радиусом 30 мм откладывая отрезок ЕВ, находим точку для проведения первой трисекции угла. От второй точки откладывая две отрезки ЕВ, имеем вторую точку трисекции угла. После этого проводится трисекции угла α.
Наше построение трисекции заданного угла показали, что хорды (по дуге R3=30 мм) упирающие к трисекциям практически равны. То есть разработанные нами способ и методика обеспечывают преимущественно высокой точности проведения трисекции угла.
Компьютерный анализ этого способа полностью поттвердил правильность нашего вывода, рис.3.
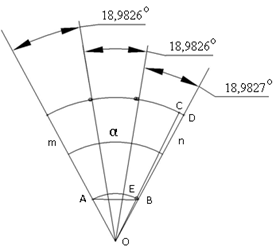
Рис. 3.
Для этого за практической точностью 1/3 угла α, мывзяли компьютерное построение трисекции данного угла равной 18,98260. Из 3- рисунка видно, что первый и второй углы равны, а третий угол отличаются на величину +0,0001°.
Таким образом, теоретически обоснованный и практически реализо-ванный новый способ обеспечивает высокую точность и простату графических построений проведения трисекции угла. Т. е. практически можно считать точным.
Если заданный угол значительно больше, то остаток дуги СD также больше. В таких случаях рекомендуется раствор циркуля взять чут больше хорды АВ первой дуги.
Если дуга ЕВ значительно меньше, то проводя дугу радиусом 9R = 90 мм, получим дугу три раза длиннее СD. Откладывая хорды дуги СD на вновь построенной дуге, получим точку К. Праводим прямую ОК, которая и делить дугу СD на 1/3. Аналогически выполняя третье действие выше изложонного способа построим трисекцию данного угла, рис.4. Результаты которого оказались одинаковыми как на рис. 3.
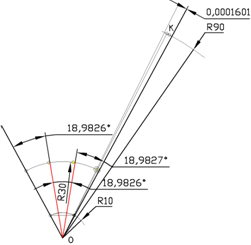
Рис. 4.
Этим способом и методом можно делить заданный угол, на любое равное n ное число. По этому новый способ можно называть универсальным. Если n =7 или n =9, то радиусом второй дуги берётся 70 или 90 мм.
Литература:
1. Атаджанов Р. К. Элементы конструктивной геометрии. Тошкент: Ўқитувчи, 1974 –С. 14–19.
2. М.Мамасалиев, Н.Гулямова, Т.Рихсибаев. «Универсальный способ проведения трисекции угла». Севастополь. Тезисы докладов ХI Международной студенческой научно-теоретической конференции, 2008. -С. 32–33.







