Введение
На сегодняшний день биоинформатика является интенсивно развивающейся областью исследований на стыке биологии и информатики. Она помогает решать задачи анализа биологических последовательностей, таких как ДНК, РНК и белки с помощью компьютеров, что ускоряет процесс получения результатов в научных областях, связанных с исследованиями уже имеющихся биологических последовательностей, и секвенированием новых.
В основе многих операций с биологическими последовательностями лежит их сравнение. Сравнение последовательностей состоит в поиске их схожих и отличающихся частей. Основными задачами, решаемыми при сравнении биологических последовательностей, являются определение подобия двух последовательностей как меры того насколько последовательности сходны, и выравнивание двух последовательностей для определения соответствия их знаков и подстрок в соответствующих позициях [1].
Согласно [2] выравнивание — это процедура сравнения двух или более последовательностей для поиска сходных участков последовательностей.
В дальнейшем под выравниванием понимается парное выравнивание последовательностей.
Основными алгоритмами выравнивания биологических последовательностей являются:
- алгоритм Нидлмана-Вунша для глобального выравнивания биологических последовательностей;
- алгоритм Смита-Ватермана для локального выравнивания биологических последовательностей.
Данные алгоритмы используют принцип динамического программирования для нахождения оптимального выравнивания биологических последовательностей.
Задача динамического программирования сводится к разбиению основной задачи на более мелкие подзадачи, и затем объединению их решений в общее решение задачи. В некоторых случаях все множество подзадач имеет одинаковый алгоритм решения. Тогда множество подзадач может быть разбито на несколько непересекающихся подмножеств, так, чтобы в одном подмножестве оказались независящие друг от друга подзадачи, которые могут быть решены параллельно. Задачи подобного типа могут быть решены с использованием параллельных вычислительных структур, таких как SIMD‑процессоры. Недостаток подобного способа решения состоит в его высокой стоимости. Более доступным вариантом является использование параллелизма на уровне GPU.
Решения данной задачи с использованием CUDA рассматривалось в [3], на примере выравнивания белков, и в [4] при исследовании сворачивания РНК. Однако вопросы оптимизации обращения к глобальной памяти в работах [3,4] не рассматривается. В [3] рассматривается использование разделяемой памяти для обращения к элементам матрицы, но размер разделяемой памяти ограничен, что ограничивает использование больших блоков потоков.
В дальнейшем в предлагаемой статье будет описан способ оптимизации обращения к глобальной памяти на GPU с использованием программной модели CUDA при решении задачи динамического программирования.
SIMT-архитектура
Архитектура NVIDIA GPU построена на масштабируемых многопоточных потоковых мультипроцессорах (SM). Мультипроцессор предназначен для выполнения сотен тысяч потоков параллельно. Для управления таким количеством потоков разработана уникальная архитектура, называемая SIMT (Single Instruction Multiple-Thread). Инструкции в данной архитектуре являются конвейерными, что позволяет использовать как параллелизм на уровне команд, так и параллелизм на уровне потоков. Мультипроцессор создает, управляет и выполняет потоки группами по 32 параллельных нити. Такая группа называется варпом (warp). Все нити варпа начинают выполняться с одного адреса, но каждая нить имеет свой счетчик команд и регистр состояний, и может выполнять независимую ветвь программы. Полуварп является половиной варпа [5], эта единица деления варпа была введена с целью оптимизации обращения к множествам нитей.
На GPU глобальная память обладает высокой латентностью, поэтому для достижения большей эффективности выполнения приложения доступ к ней необходимо оптимизировать. Основными способами оптимизации обращения к памяти являются выравнивание по границе 4-, 8-, 16-байтным словам, и объединение запросов всех нитей полуварпа или всего варпа в одно обращение к непрерывному блоку памяти. При этом блок должен быть выровнен по своему размеру [6].
Задача динамического программирования
Согласно [7] Существует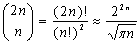 
глобальных выравниваний двух последовательностей длины n. Перебрать все возможные выравнивания для поиска оптимального физически невозможно, даже для малых значений n. Поэтому алгоритмы поиска оптимального выравнивания основаны на методе динамического программирования. Данный метод занимает центральное место в анализе биологических последовательностей.
Для глобального выравнивания биологических последовательностей рассмотрим алгоритм Нидлмана-Вунша, предложенный в [8] и усовершенствованный в [9]:
Алгоритм заключается в заполнении матрицы F. В ячейках Fi,j матрицы содержатся веса оптимального выравнивания между подпоследовательностями длины i и j.
Вначале заполняются элементы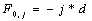 
и 
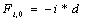. Далее матрица заполняется согласно рекуррентному соотношению:
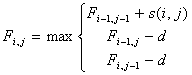, (1)
где
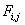— элемент матрицы F;
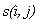— функция, возвращающая значение 1, если i и j элементы последовательностей равны, 0 в противном случае;
d — штраф за разрыв.
Если в формуле (1) выбран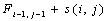 
, то сравниваются 2 элемента последовательностей, иначе если выбран 
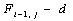или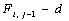 
то удаляется j-й символ второй последовательности или i-й символ первой соответственно.
После этого производится обратный проход по матрице от правой нижней ячейки и по пути оптимального выравнивания полученном на предыдущем шаге для нахождения оптимального выравнивания двух последовательностей.
Создание параллельного алгоритма
Алгоритм заполнения матрицы можно распараллелить. Для этого согласно методологии канонического отображения [10] необходимо разработать граф зависимости.
Граф зависимости элементов матрицы представлен на рисунке 1.
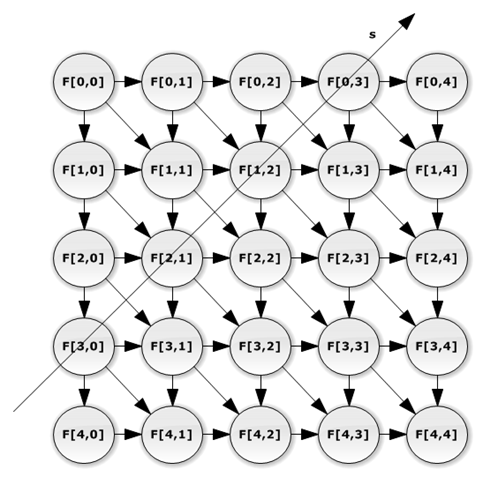
Рис. 1. Граф зависимости
На рисунке 1 задано решетчатое дискретное пространство. В узлах решетки располагаются вычисления, которые могут быть назначены реальным или виртуальным вычислительным узлам (например, моделируемым нитями). Связи между вычислениями направленные и задают зависимости по данным в ходе вычисления. В данном пространстве можно выделить множество гиперплоскостей, каждая гиперплоскость объединяет множество вычислений, которые могут быть выполнены одновременно. Текущая гиперплоскость объединяет вычисления, которые производятся в текущий момент времени. Текущую гиперплоскость будем задавать с помощью вектора s.
Далее согласно методологии канонического отображения необходимо составить граф потока сигналов (рисунок 2)
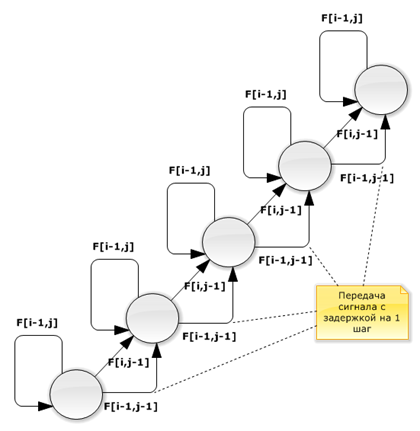
Рис 2. Граф потока сигналов
На рисунке 2 решетчатое пространство, представленное на рисунке 1, спроецировано на гиперплоскость, параллельную вектору s. В узлах графа зависимости расположены процессорные элементы. Каждому процессорному элементу назначен столбец графа зависимости. Дугами показаны передачи сигналов между процессорными элементами.
Данная схема плоха тем, что при использовании программной модели CUDA элементы матрицы будут сохраняться в глобальную память в отдельных транзакциях, так как они не расположены в непрерывном участке памяти.
Для оптимизации обращений к глобальной памяти элементы матрицы должны быть переупорядочены, как представлено на рисунке 3.
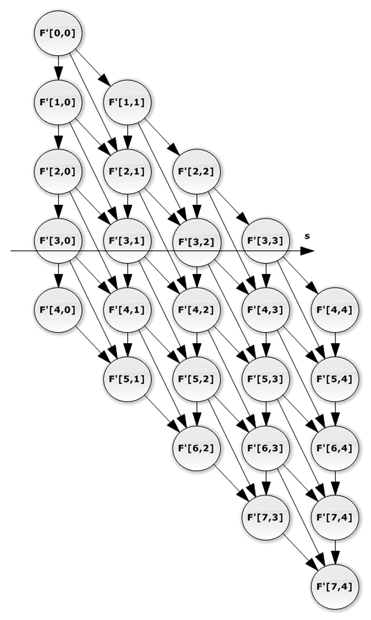
Рис. 3. Модифицированный граф зависимости
На рисунке 3 гиперплоскости вычислений расположены вдоль строк матрицы, поэтому при сохранении результатов вычислений в узлах решетки в глобальную память транзакции могут быть объединены, что ускорит работу алгоритма.
Составим граф потока сигналов для данного решетчатого пространства.
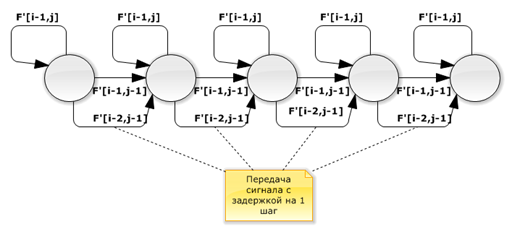
Рис. 4. Модифицированный граф потока сигналов
Как видно из рисунков оригинальный и модифицированный графы зависимости и соответствующие им графы потока сигналов изоморфны. Поэтому модель вычислений осталась прежней.
Аналогичная идея оптимизации обращения к памяти была представлена в [11], однако достаточно простого решения проблемы не было предложено.
Нумерация элементов матрицы
Для того чтобы элементы матрицы располагались как представлено на рисунке 2 необходимо их перенумеровать. Нумерация — это отображение множества натуральных чисел на соответствующее множество [12]. Основное применение нумераций — построение эффективной модели представления данных в памяти [13].
В нашем случае под нумерацией понимается взаимно однозначное отображение из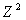 
в .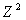
Введем отношение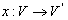 
, где 
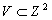и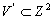 
, то есть паре чисел 
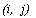ставится в соответствие пара 
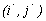, значения которых могут быть вычислены по формуле:
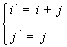
Обратная нумерация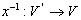 
задается формулой
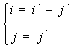
Данная нумерация переносит элементы матрицы с диагоналей параллельных побочной диагонали в строки, так что они находятся в соседних позициях.
Свойства нумерации:
1) номер строки в новой матрице совпадает с номером итерации цикла;
2) номера столбцов исходной и новой матриц совпадают;
3) число строк новой матрицы равно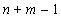 
;
4) число столбцов в матрицах совпадает.
Из свойств 1 и 2 следует, что во время вычисления значений матрицы нет необходимости вычислять пару 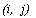, а значения соседних элементов, необходимых для вычисления, определяются по формулам:
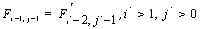
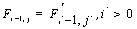
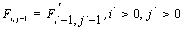
Из свойств 3 и 4 следует, что размер дополнительной памяти, необходимый для организации матрицы равен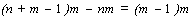 
слов. Поэтому для более эффективного расхода памяти и лучшей загрузки процессора необходимо чтобы выполнялось условие 
.
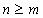Реализация алгоритмов
Рассмотрим реализацию алгоритма Нидлмана-Вунша на языке CUDA для семейства GPGPU Nvidia, поддерживающего данную технологию. Язык CUDA является расширением языка C. В него добавлены средства запуска ядра и API для работы и управления GPU, управления выполнением нитей ядра и передачей данных между нитями и между CPU и GPU. Программа на языке CUDA компилируется с помощью специального компилятора, который разделяет программный код для GPU и CPU. Программный код для GPU компилируется с данным компилятором в объектный или ассемблерный код. А программный код для CPU компилируется стандартным C компилятором, затем линковщик соединяет объектные файлы в программу.
Каждая нить вычисляет отдельный столбец матрицы в цикле. Для вычисления значений матрицы на CUDA необходимо, чтобы нити работали синхронно. Для этого внутри цикла необходимо поставить барьерную синхронизацию. Однако для упрощения межпроцессорного взаимодействия можно синхронизировать только нити внутри блока, межблочная синхронизация стандартными средствами CUDA невозможна. Поэтому для вычисления элементов матрицы воспользуемся следующим методом, предложенным в [14]. Схема вычислений представлена на рисунке 5.
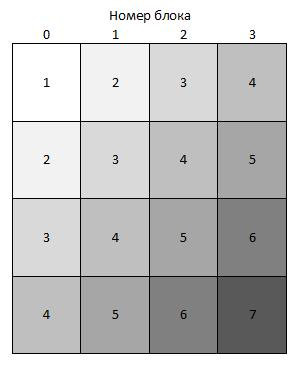
Рис. 5. Схема вычислений
Каждый блок из n нитей вычисляет фрагмент матрицы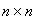 
, после чего ядро перезапускается. Блоки, отмеченные на рисунке одинаковыми номерами, могут быть запущены в одном ядре. В данном случае получается параллелизм как на уровне нитей, так и на уровне блоков.
В алгоритме Нидлмана-Вунша для вычисления значения элементов матрицы методом динамического программирования необходимо знать значения трех соседних элементов матрицы, вычисленных на предыдущих шагах. Их необходимо прочитать из глобальной памяти GPU. Так как данная операция выполняется достаточно долго, можно передавать вычисленные значения напрямую между нитями, минуя глобальную память. Для этого необходимо воспользоваться разделяемой памятью. Разделяемая память имеет небольшой размер, и поэтому находится в кэше, что ускоряет доступ к ней. Однако полностью избавиться от чтения из глобальной памяти невозможно, т. к. в начале работы ядра необходимо проинициализировать разделяемую память, прочитав в нее из глобальной значения полученные ранее.
Скорость выполнения программы зависит от размера блока. Чем больше блок, тем меньше число запусков ядра, что ускоряет работу программы. Однако чем больше блок тем больше накладные расходы связанные с барьерной синхронизацией, и тем больший объем разделяемой памяти необходим блоку, из-за чего разделяемая память может не поместиться в кэш полностью.
Исходный код программы расположен в git-репозитории по адресу https://bitbucket.org/apotapoff/sequence_alignment.git версия 0.0.1. Эксперименты проведены на платформе NVIDIA GeForce GTX 460.
На рисунке 6 показаны графики времени выполнения ядра в зависимости от размеры входных данных и размера блока.
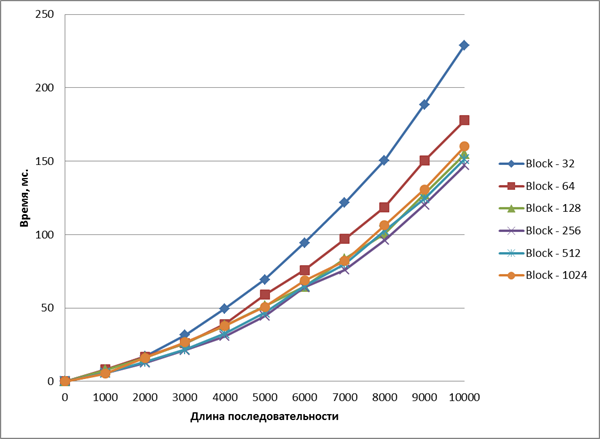
Рис. 6. Время выполнения ядра неоптимизированного алгоритма
Из рисунка видно, что наиболее оптимальный размер блока составляет 256 потоков. При увеличении блока увеличиваются накладные расходы времени на организацию работы блока.
После переупорядочивания элементов матрицы транзакции к глобальной памяти для потоков варпа (полуварпа) объединяются, что дает увеличение скорости обращения к глобальной памяти в 32 (16) раза. Для оптимизированного алгоритма также необходима синхронизация потоков, для этого воспользуемся такой же схемой вычисления, как и в предыдущем случае. Данное решение увеличивает число запусков ядра, что влечет за собой увеличение времени работы алгоритма, однако более лучшего способа обойти данное ограничение архитектуры, пока не найдено.
Для уменьшения числа обращения к глобальной памяти воспользуемся также передачей данных между нитями через разделяемую память.
Результаты экспериментов представлены на рисунке 7.
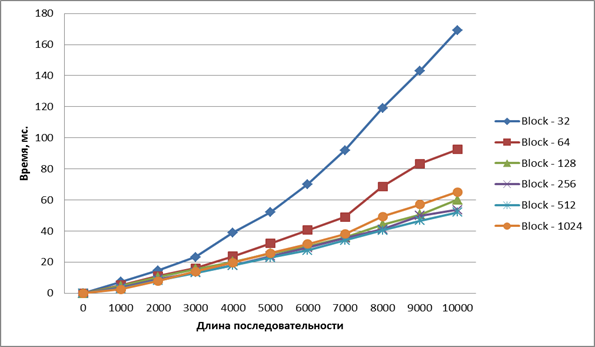
Рис. 7. Время выполнения ядра оптимизированного алгоритма
Согласно рисунку, время работы алгоритма снижается при увеличении числа потоков в блоке. Однако при числе нитей 256, 512 и 1024 ускорения выполнения не наблюдается.
Сравним скорость выполнения алгоритмов при числе потоков в блоке равном 256 (Рисунок 8).
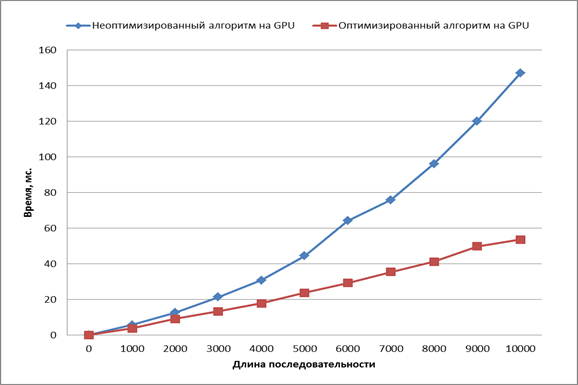
Рис. 8. Сравнение скорости работы алгоритмов
Как видно из графика, оптимизированный алгоритм работает быстрее неоптимизированного, и на последовательностях ДНК длинной 10000 элементов его время выполнения в 3,5 раза меньше.
Сравним размер необходимой глобальной памяти для работы алгоритмов (Рисунок 9)
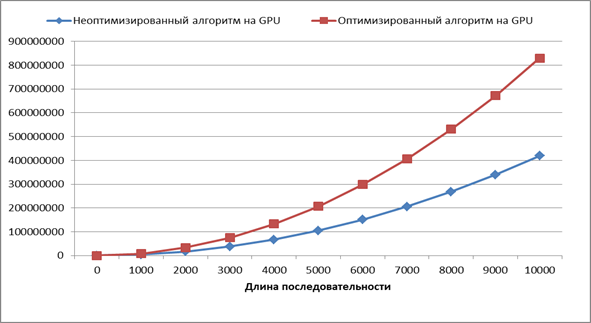
Рис. 9. Сравнение размера памяти для работы алгоритмов
Размер памяти требуемой алгоритмам имеет одинаковую асимптотику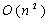 
, однако для оптимизированного алгоритма требуется в два раза больше памяти, что ограничивает его использование на больших последовательностях. Однако память является менее критичным ресурсом, чем время. Обойти данное ограничение можно, либо увеличив количество памяти на GPU, либо используя кластеры из GPU.
Вывод
В работе рассмотрен метод переупорядочивания элементов матрицы динамического программирования для алгоритмов выравнивания биологических последовательностей, оптимизирующий обращение к глобальной памяти на GPU. Предложен способ нумерации элементов матрицы. И проведены эксперименты, доказывающие, что переупорядочивание элементов матрицы дает уменьшение времени работы алгоритма за счет объединения транзакций к глобальной памяти GPU в каждом варпе.
Литература:
1. Сетубал Ж, Мейданис Ж. Введение в вычислительную молекулярную биологию. — Москва-Ижевск: НИЦ «Регулярная и хаотическая динамика», Институт компьютерных исследований, 2007. — 420 с.
2. Mount DM. (2004). Bioinformatics: Sequence and Genome Analysis (2nd ed.). Cold Spring Harbor Laboratory Press: Cold Spring Harbor, NY.
3. T. R. P. Siriwardena & D. N. Ranasinghe «Global Sequence Alignment using CUDA compatible multi-core GPU», Information and Automation for Sustainability (ICIAFs), 2010 5th International Conference on, 2010
4. Peter Steen, Robert Giegerich, Mathieu Giraud, «GPU parallelization of algebraic dynamic programming», Proceedings of the 8th international conference on Parallel processing and applied mathematics: Part II, 2010
5. CUDA C programing Guide.
6. Боресков А. В. «Параллельные вычисления на GPU. Архитектура и программная модель CUDA: учеб. пособие» — М.:Издаельство Московского университета, 2012–336 с.
7. Дурбин Р., Эдди Ш., Крог А., Митчисон Г. Анализ биологически последовательностей. — М.-Ижевск: НИЦ «Регулярная и хаотическая динамика», Институт компьютерных исследований, 2006. — 480 с.
8. Saul B. Needleman, Christian D. Wunsch «A general method applicable to the search for similarities in the amino acid sequence of two proteins», Journal of Molecular Biology 48, 1970.
9. Osamu Gotoh «An improved algorithm for matching biological sequences»», Journal of Molecular Biology 162, 1982.
10. Кун С. Матричные процессоры на СБИС: Пер. с англ. — М.: Мир, 1991. — 672 с.
11. Singbo Jung GPU data-parallel computing computing of sequence alignment using CUDA, 2008.
12. Ершов Ю. Л. Теория нумераций — М., 1977. — 416 с.
13. Линьков В. М. Нумерационные методы проектирования систем управления данными: Монография — Пенза: Изд-во Пенз. гос. техн. ун-та, 1994. — 156 с.
14. S. Che, M. Boyer, J. Meng, D. Tarjan, J. W. Sheaffer, and K.Skadron. A performance study of general-purpose pplications on graphics processors using cuda. [Online]. Available:http://citeseerx.ist.psu.edu/viewdoc/summary?oi=10.1.1.143.4849
