В данной статье представлено решение в напряжениях некоторых осесимметричных задач для упругого пространства с единственной сферической неоднородностью единичного радиуса (которая может представлять собой полость, упругое или жесткое включение) при одноосном растяжении на бесконечности.
Сферические неоднородности являются концентраторами напряжений (например, включения в композиционных материалах), определение напряженно-деформированного состояния вблизи которых имеет важное практическое значение. Часто такие задачи являются осесимметричными и обычно решаются при помощи уравнений Ламе [6–11]. В отличие от известных подходов к решению подобных задач [1] в данной работе использована постановка и метод решения, предложенный в работах [2–5]. Суть подхода состоит в следующем:
1. Основными уравнениями являются два уравнения равновесия и два уравнения сплошности, записанные в напряжениях. В напряжениях записываются статические и кинематические граничные величины.
2. Решение представлено в виде степенных рядов по косинусу угла между осью вращения и радиусом сферы. Коэффициенты этих рядов, зависящие от радиальной координаты сферической системы координат, вычисляются при помощи системы обыкновенных дифференциальных уравнений типа Эйлера.
Преимущество даннного подхода заключается в том, что неизвестные данной системы совпадают с кинематическими и статическими краевыми величинами, а это, в свою очередь, упрощает удовлетворение краевых условий на сферической поверхности.
Постановка задачи для трех задач отличается только граничными условиями, для её формулировки воспользуемся соотношениями, приведенными в [2].
Тензор напряжений представлен в виде
(1)
вектор перемещений
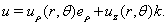
Здесь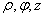 
— цилиндрические координаты с ортами 
; 
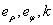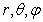— сферические координаты с ортами 
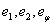(см. рисунок 1). Ось 
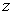совпадает с осью вращения тела.
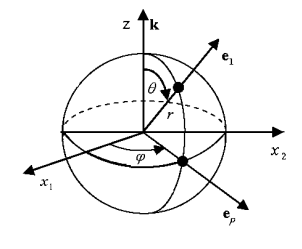
Рис. 1. Система координат
Таким образом, тензор напряжений хоть и записан в цилиндрических координатах, но независимыми аргументами являются координаты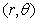 
. Компоненты тензора напряжений (1) удовлетворяют следующим дифференциальным уравнениям:
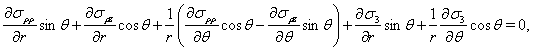
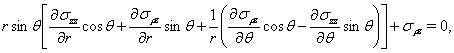
(2)
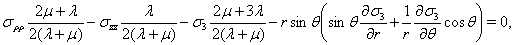
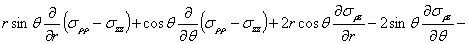
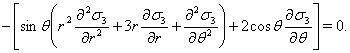
Здесь
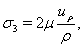
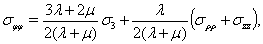(3)
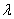и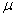 
-физические постоянные Ламе.
Осевую составляющую перемещения находим при помощи следующих уравнений [3]:
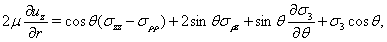
(4)
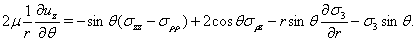
Наличие в пространстве:
- полости означает, что на границе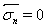 
при 
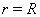, где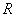 
— радиус полости.
- жесткого включения означает, что на границе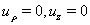 
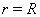при , где 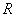— радиус жесткого включения.
- упругого включения означает, что в данном случае на границе упругого включения должны выполняться условия сопряжения: (индекс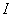 
соответствует матрице, а 
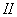-включению)
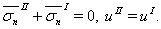(5)
Считаем, что на бесконечности задано напряженное состояние
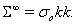
Искомые напряжения представим следующим образом:
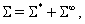(6)
где
Тогда компоненты тензора (6) можно представить в виде
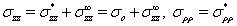
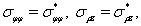
а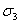 
в соответствии c (3)
Компоненты тензора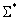 
удовлетворяют системе (2). Соответствующие граничные условия при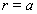 
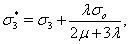(7)
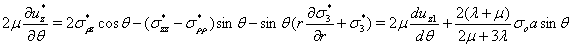. (8)
Рассматриваемая задача симметрична относительно плоскости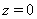 
, и решение будем искать в виде рядов [4]
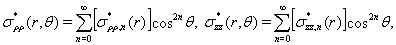
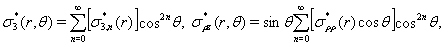(9)
Далее систему (2) преобразуем путем введения новых величин по формулам
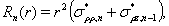
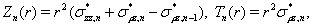(10)
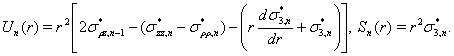
В итоге основная система уравнений примет вид системы обыкновенных дифференциальных уравнений типа Эйлера:
,
,
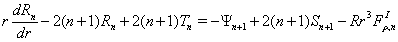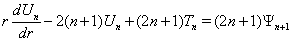, (11)
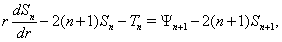
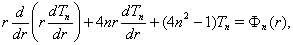
где
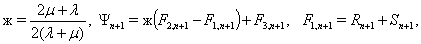
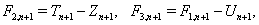
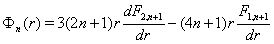
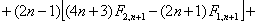
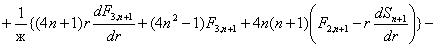
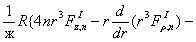
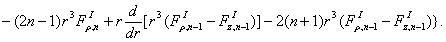
Решение системы уравнений (11) при отсутствии массовых сил и конечном числе членов ряда (9) представляют собой конечные ряды по отрицательным и положительным степеням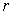 
, неопределенный коэффициенты которых находятся из граничных условий. Кроме того, эти ряды должны тождественно удовлетворять условию
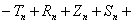
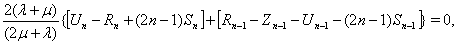
Краевые условия в терминах системы имеют вид:
для полости
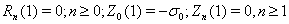, (12)
для жесткого включения
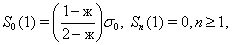(13)
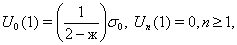
упругого включения
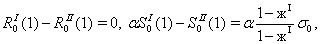(14)
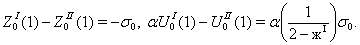
Во всех трех задачах оказалось, что в рядах (9) можно удержать не более трех членов ряда. Так как все искомые величины системы (11), как было сказано выше, представляют собой конечные ряды по отрицательным и положительным степеням 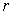, то неопределенные коэффициенты величин 
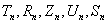с учетом вида граничных условий определяются из системы линейных алгебраических уравнений.
В случае, упругого включения, когда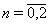 
, решение системы (11) при граничных условиях (14) будет следующим:
,
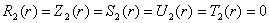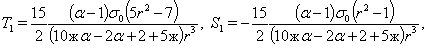
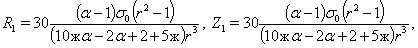
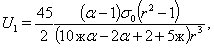
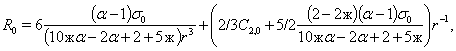
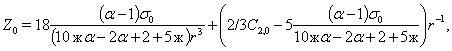
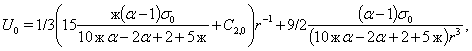
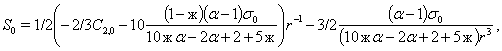
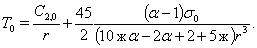
Соответственно по обратным формулам к (15), а именно
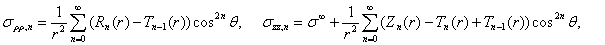
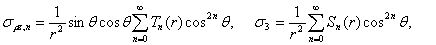(15)
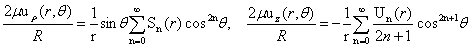
можем записать искомые напряжения и перемещения. Далее для краткости изложения ниже представлены графики напряжения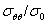 
на границе упругого включения в зависимости от 
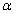. Как видно из рис. 2, график при 
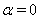совпадает с графиком 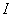, что соответствует случаю, когда шаровидная неоднородность является полостью. Кроме того, график при 
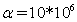совпадает с графиком 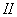, что соответствует случаю, когда шаровидная неоднородность является жестким включением. Точка пересечения графиков 
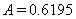, соответствует примерно 
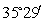, полученные аналитические решения совпали с [1], но различие сред описывается одним параметром 
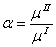, что удобнее для численных расчетов. Корме того, из графика видно, что пр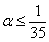и 
и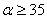 
упругим включением можно пренебречь и рассматривать задачу как частный случай полости или жесткого включения соответственно.
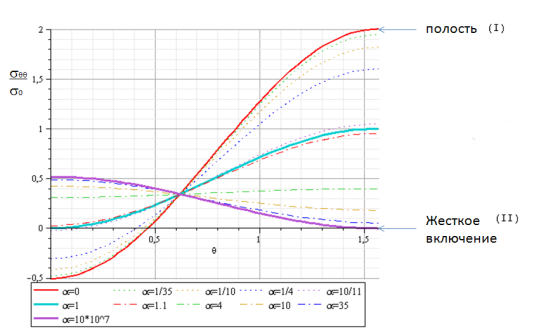
Рис. 2: График напряжения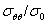
Предложенный подход к решению осесимметричных задач для сферы можно использовать и несферических неоднородностей в упругом пространстве.
Литература:
1. Goodier J. N. Concentration of stress around spherical and cylindrical inclusions and flaws. J Appl Mech 1933;APM-55–7:39–44.
2. Гасратова Н. А., Шамина В. А. Решение в напряжениях линейной осесимметричной задачи для сферы и упругого пространства со сферической полостью // Вестн. С.-Петерб. ун-та. Сер. 1: Математика, механика, астрономия. 2008. Вып. 2 С. 122–128.
3. Шамина В. А. Постановка линейной осесимметричной задачи механики деформируемого тела в напряжениях // Вестн. С.-Петерб. ун-та. Сер. 1: Математика, механика, астрономия. 2000. Вып.1 (№ 1). С. 145–148.
4. Гасратова Н. А., Шамина В. А. Об одном подходе к решению осесимметричных задач линейной теории упругости // Вестн. С.-Петерб. ун-та. Сер. 1: Математика, механика, астрономия. 2007. Вып. 2. С. 101–107.
5. Гасратова Н. А. Напряженно-деформируемое состояние упругого пространства со сферическим жестким включением. //Вестник С.-Петерб. ун-та. Сер.10, 2009. С. 14–18,
6. Hamid R. Sadraie, Steven L. Crouch, Sofia G. Mogilevskaya. A boundary spectral method for elastostatic problems with multiple spherical cavities and inclusions//Engineering Analysis with Boundary Elements 31 (2007) p.425–442.
7. Noda Nao-Aki, Nozomu Ogasawara, Tadatoshi Matsuo. Asymmetric problem of a row of revolutional ellipsoidal cavities using singular integral equations.//International Journal of Solids and Structures 40 (2003) p. 1923–1941.
8. Noda Nao-Aki, Yasuhiro Moriyama. Stress concentration of an ellipsoidal inclusion of revolution in a semi-infinite body under biaxial tension. //Archive of Applied Mechanics 74 (2004) p. 29–44.
9. Edwards R. H. Stress concentrations around spherical inclusions and cavities.// J. Appl. Mech., 1951, 18, p. 19–30.
10. Sadowsky M. A., Sternberg E. Stress concentration around a triaxial ellipsoidal cavity.// J. Appl. Mech., 1949, v. 16, p. 149–157.
11. Олегин И. П. Осесимметричное напряженное состояние в трансверсально-изотропной упругой среде с двумя жесткими эллипсоидальными включениями//Сибирский журнал индустриальной математики. Январь–март, 2002. Том V, № 1(9).С.127–132.
