Математическая модель логистической популяции на линейном ареале

Формулируется математическая модель одиночной популяции на отрезке, представляющая собой краевую задачу для нелинейного дифференциального уравнения в частных производных. Исследуются на устойчивость стационарные решения, решение стационарного уравнения представлено в квадратурах. Предлагается алгоритм численного решения нелинейной краевой задачи. Проведено исследование влияния различных параметров на поведение решений.

Ключевые слова: популяция, краевые задачи, математическое моделирование

Введение. Теоретические позиции, лежащие в основе большинства сегодняшних математических моделей взаимодействующих популяций, закладывались в работах Лотка и Вольтерра [1, 2, 4]. Начиная с 60х годов 20 века, предлагаются и исследуются модели с отличными от вольтеровских кинетическими функциями, описывающими взаимодействие популяций [1, 2, 9, 14, 19, 20, 22, 25]. Большая часть моделей, посвященных динамике взаимодействующих популяций, представлена задачей Коши для системы обыкновенных дифференциальных уравнений. Точечные модели предполагают, что среда обитания является гомогенной и плотность популяции не зависит от пространственных координат. Реальные популяции существуют на ограниченных территориях и в ограниченных пространственных объемах с различными свойствами среды в разных ее частях. Гетерогенные свойства среды, внутренняя социальная организация популяции, сформировавшиеся в эволюционном процессе стратегии выживания, вызывают, по крайней мере, у некоторых особей, необходимость к расселению. Распространение их по территории происходит, как правило, от мест с большей концентрацией особей в места с меньшей их концентрацией [3, 5, 8, 10–13, 15–17, 21, 23, 26, 27]. Математические модели в этом случае разрабатываются на основе аппарата уравнений в частных производных [9, 18, 19, 22, 25, 30, 31].

Механизмы спонтанного распространения животных на территории наиболее хорошо изучены на примере мелких млекопитающих [10, 21, 23]. Выделяют 2 основных типа расселения особей по территории: до насыщения ареала особями и при насыщении. До насыщения происходит расселение особей, чувствительных к росту плотности популяции, стремящих занимать участки с минимальной плотностью. При насыщении территории начинается вытеснение с территории особей низкого социального ранга, обреченных на гибель при оседлом образе жизни, а также молодых особей из-за нехватки ресурсов [10, 16, 21, 23]. Т. е., процесс распространения популяции на территории, вызванный этими причинами, можно рассматривать как случайное индивидуальное или групповое перемещение особей.

В работе рассматривается модель одиночной обобщенной логистической популяции на неограниченном трофическом ресурсе, находящейся на линейном ареале (на прямой). Для описания динамики численности популяции используется эволюционное уравнение.

Модель обобщенной логистической популяции. Первой математической моделью, описывающей эволюцию изолированной популяции с ограниченным ростом ее численности, была, по-видимому, модель Ферхюльста [1]. Обобщением модели Ферхюльста является модель обобщенной логистической популяция [22], закон роста которой описывается уравнением

где непрерывная и дважды дифференцируемая функция 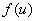 удовлетворяет следующим условиям:

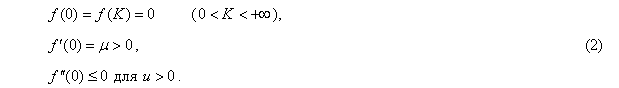
Функция 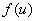 называется локальной скоростью роста популяции,  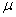— мультизианским параметром,  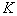— емкостью среды [1, 2, 18, 30].

Условие 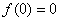 естественное, поскольку в отсутствие особей популяция возникнуть не может, условие  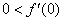обеспечивает рост возникшей популяции, а условие  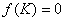— ограниченность численности популяции сверху. Стационарная точка  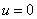является неустойчивой, а точка  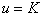— устойчивой. Поэтому все решения уравнения (1) при выполнении условий (2) будут монотонно возрастающими на промежутке 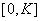, выходить из точки  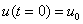и стремиться к значению  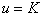при 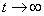. В дальнейшем за единицу измерения численности популяции принимается емкость среды, т. е. .

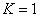Примерами моделей обобщенной логистической популяции являются логистическая — 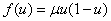, Розенцвейга — 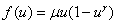. Для моделей Свирижева [2, 22]  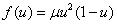и ее обобщения  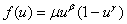(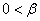, 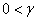) не выполняется условие 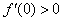. Но, как и в случае логистической популяции, стационарная точка  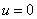будет неустойчивой, а  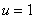— устойчивой.

Диффузионная модель. Вприроде в качестве примеров протяженных в одном направлении ареалов, в которых живут различные виды флоры и фауны, могут служить обочины полей и дорог, трубопроводы, реки и т. п. [13, 15, 17, 23]. В модели этот тип распространения популяции можно рассматривать как распространение популяции вдоль прямой. В этом случае процесс распространения особей можно описать эволюционным уравнением [18, 30]

где 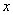 — декартова координата, а функция  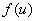соответствует локальной скорости изменения численности популяции. Функция  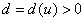характеризует подвижность особей. В этой модели учитывается эффект вытеснения особей или их уплотнения при изменении численности популяции. Если 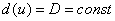, то естественно считать, что перемещение особей на территории происходит случайным образом. В качестве одного из вариантов зависимости  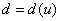в [30] предлагается  ().

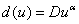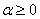К уравнению (3) для случая отрезка длины 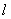 необходимо добавить начальные и граничные условия. В качестве начальных условий задается значение функции  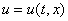в начальный момент времени: при  .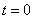

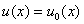В качестве граничных условий рассматриваются два варианта:

Условие обращения в ноль функции 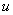 на границе отрезка соответствует невозможности существования популяции в этой точке. Условие же обращения в ноль производной  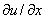на границах отрезка (условие наполнения среды [18, 19, 30]) допускает свободный рост численности популяции.

Если в качестве начальных условий для уравнения (3) взять 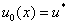, где 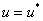 корни уравнения 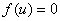, то функция  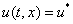будет решением этого уравнения при граничных условиях (4). Если уравнение  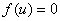имеет несколько решений, то и уравнение (3) при граничных условиях (4) может иметь неединственное решение.

Стационарное решение. Уравнение (3) пр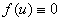и  и 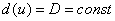 переходит в уравнение диффузии и его решение при стационарных граничных условиях со временем стремится к решению статической задачи независимо от значения искомой функции в начальный момент времени [24]. При рассматриваемых вариантах граничных условий (4) и (5) это будет тривиальное решение. Для нелинейного уравнения (3) это свойство может отсутствовать.

Стационарное решение нелинейного уравнения (3) должно удовлетворять дифференциальному уравнению

Это уравнение при естественном требовании 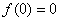, накладываемом на функцию 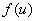, при граничных условиях (4) и (5) будет иметь тривиальное решение.

Если уравнение (6) умножить на 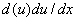 и проинтегрировать, то можно получить квадратуру [9, 18]

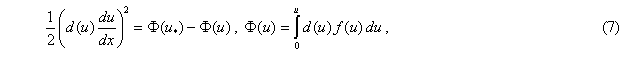
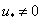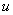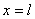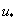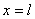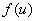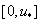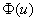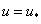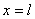где  — значение функции  в точке . Такой выбор постоянной интегрирования  обеспечивает выполнение граничного условия при  в (4) и (5). Если функция  на промежутке  неотрицательна, а для обобщенной логистической популяции это выполняется, то  в силу этого будет монотонно возрастающей функцией с экстремальным значением в точке  (при ). Поэтому уравнение  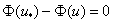может иметь только один корень на промежутке  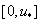и, соответственно, удовлетворить первому условию в (4), как это следует из (7), можно только в том случае, если решением будет 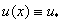. В этом случае решениями уравнения (6), при граничных условиях (4), будут являться корни уравнения 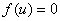. Для обобщенной логистической популяции ими являются  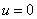и .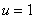

Поскольку функция 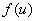 на промежутке  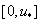принимает положительные значения, то решение  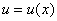уравнения (6) с граничными условиями (5) в точке  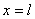принимает экстремальное значение. При этом на промежутке  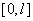должны выполняться условия 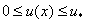. С учетом этого из (7) следует зависимость 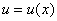, выраженная в виде интеграла

.

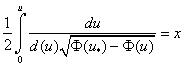Это решение будет удовлетворять граничному условию 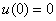, если выполняется равенство

в котором неизвестной величиной является 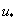 и, соответственно, (8) рассматривается как уравнение для нахождения постоянной интегрирования .

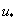Подынтегральное выражение в (8) имеет особенность в точке 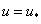, поскольку функция  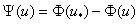обращается в ноль. Если и ее производная в этой точке равная  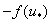будет обращаться в ноль, то  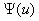будет иметь кратный корень и интеграл в левой части уравнения (8) будет расходиться. Поэтому на решениях уравнения (7)  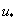не должно совпадать с корнями уравнения 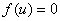. Для обобщенной логистической популяции функция  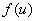обращается в ноль при 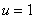. Поэтому уравнение (8) при  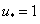решений иметь не будет. А это означает, что на решениях уравнения (6) при граничных условиях (3) выполняются условия .

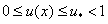Устойчивость равновесных состояний при 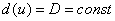. При исследовании устойчивости решения 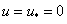, являющегося решением уравнения (3) при граничных условиях (5), и решения 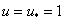, являющегося решением уравнения (3) при граничных условиях (4), естественно полагать, что в первом приближении отклонения от равновесного состояния малы. Решение уравнения (3) представляется в вид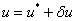е , где 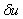 — малая по сравнению с единицей величина. Тогда из уравнения (3) с точностью до величин второго порядка малости следует уравнение для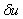

с начальным условием 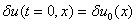, где 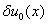 — малое отклонение от гомогенного положения равновесия такое, что .

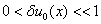Решение, удовлетворяющее граничным условиям (5), представляется в виде тригонометрического ряда

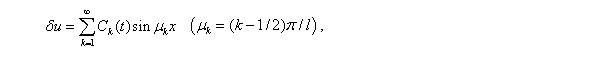
коэффициенты разложения 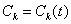 которого должны удовлетворять уравнениям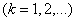

.

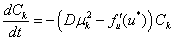Начальные условия для 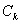 находятся из разложения в ряд Фурье функции :

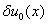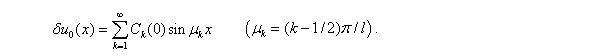
Если 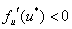, все 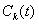 как функции времени будут стремиться к нулю при любых значениях 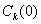. И, соответственно, решение будет устойчивым. Если 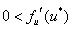, то решение будет устойчивым только в том случае, если будет выполняться неравенство 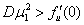. Для обобщенной логистической популяции  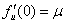и, соответственно, нулевое положение равновесия будет устойчивым при значениях коэффициента .

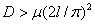Для случая граничных условий (4) решение уравнения (9) представляется в виде тригонометрического ряда

.

При положительных значениях 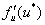 решение будет неустойчивым, при отрицательных — устойчивым.

Численные эксперименты. Построение численного решения уравнения

при граничных условиях (5) на отрезке единичной длины (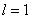) осуществлялось с применением численных методов. Уравнение аппрокисмировалось конечными разностями [7, 9, 24, 28, 29] на равномерной сетке по пространственной переменной с шагом  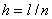и с шагом  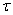по временной переменной

,                    

          (),

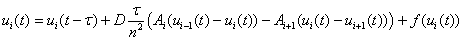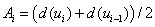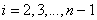для граничных условий (4) , ,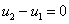

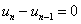а для граничных условий (5) , ,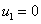

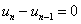где 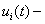 значение функции в 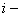ом узле в момент времени 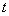, 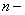число отрезков, на которые разбивался интервал интегрирования,  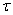— шаг интегрирования по временной переменной. Система уравнений (11) на каждом временном шаге решалась с применением метода простой итерации [6, 7, 9, 24, 28, 29]. Численная реализация осуществлялась в среде программировании пакета MatLab. Сравнение результатов осуществлялось с решениями, полученными с использованием встроенных в MatLab функций. 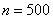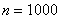Результаты на сетках с  и  с шагом интегрирования  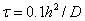по временной переменной совпали с точность до 1 %. Итерационный процесс сходился за 2–3 итерации при заданной степени точности (0.1 %) для максимальных относительных отклонений для всех узлов сетки.

Результаты основных численных экспериментов представлены на рис. 1–6. На рис. 1 отражено изменений функции 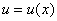 вдоль координаты для граничных условий (4) в различные моменты времени (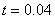, , 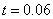, 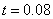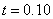) для случая 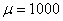, , 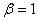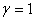. В качестве начального значения функции  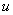бралось 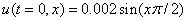. Рис. 2 соответствует случаю, когда 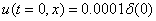, где 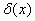 — дельта функция Дирака (, , , ).

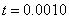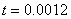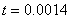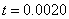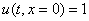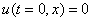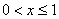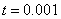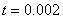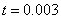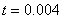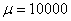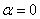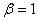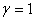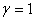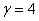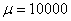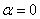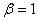Решение уравнения (10) при граничном условии  и начальном условии  при  в моменты времени , , ,  представлено на рис. 3 (, , , ), для  и  (,, ) в момент времени  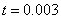приведено на рис. 4, а для случая  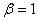в момент времен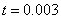и  и 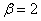 в момент времени  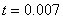(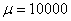, , 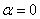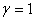) — на рис. 5. На рис. 6 отражено изменение функции  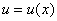в момент времен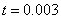и  при 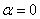 и в момент времен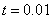и  при  (, , ).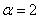

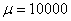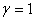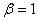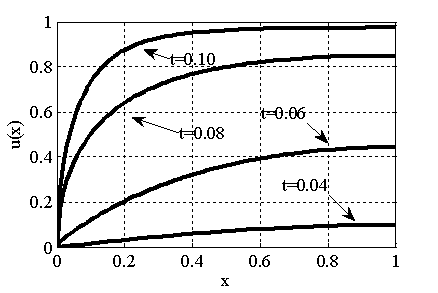
Рис. 1. Решение уравнения (10) в различные моменты времени при граничных условиях (4), , , ,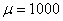

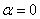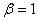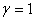
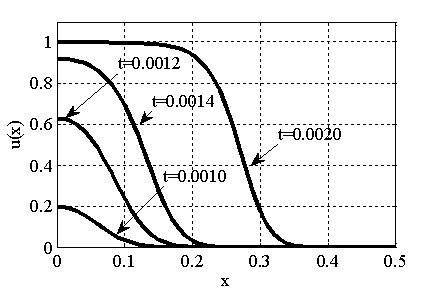
Рис. 2. Решение уравнения (10) в различные моменты времени при граничных условиях (4) и начальном условии , , , ,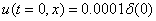

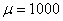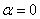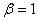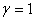
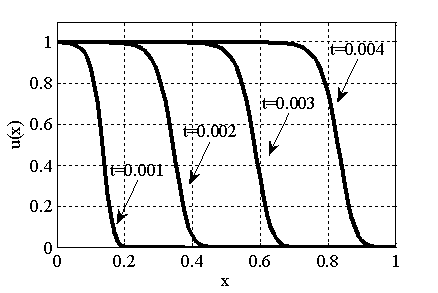
Рис. 3. Решение уравнения (10) в различные моменты времени при граничном условии 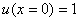 и начальном услови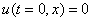и  при  (,, , )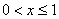

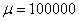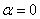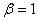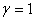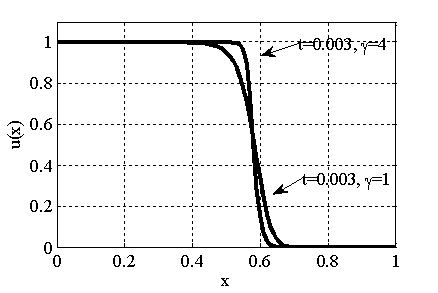
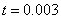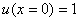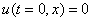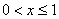Рис. 4. Решение уравнения (10) в момент времени  при граничном условии  и начальном условии  при  для значений параметра  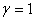и  (, , )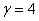

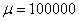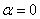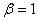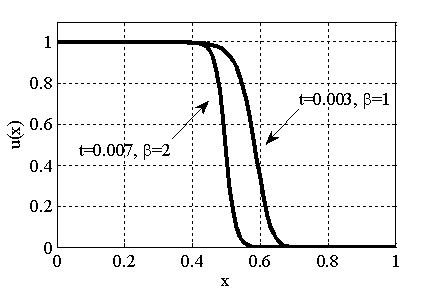
Рис. 5. Решение уравнения (10) при граничном условии 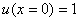 и начальном услови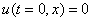и  при 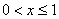 для значений параметра  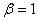в момент времен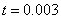и  и 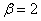 в момент времени  (, , )

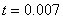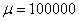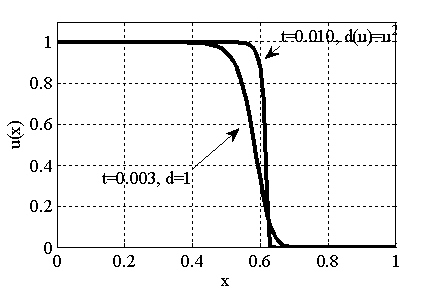
Рис. 6. Решение уравнения (10) при граничном условии 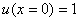 и начальном услови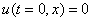и  при 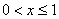 в момент времени  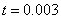(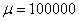, , 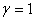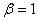) для параметра  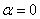и в момент времени  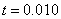для параметра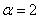

Как следует из анализов численных экспериментов логистическая популяция при малой подвижности по сравнению с высокой рождаемостью (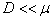) постепенно распространится на весь отрезок независимо от места ее зарождении будь то весь отрезок (рис. 1) или локальная точка (рис. 2). При этом распространение на территории может происходить в виде «волны» (рис. 3), движущейся со скоростью близкой к теоретическому значению  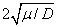для 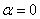 [22, 31]. Параметр  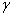в (10) несущественно влияет на «фронт» волны (рис. 4). Более существенное влияние оказывает параметр  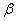— с ростом этого параметра скорость распространения волны уменьшается (рис. 5). Увеличение параметра  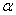приводит к уменьшению скорости распространения популяции на отрезке.

Заключение. Как следует из полученных выше результатов из «диффузионной» модели одиночной популяции следуют результаты, не содержащиеся в «точечных» моделях. Для обобщенной логистической популяции на отрезке с ограничениями роста на границах при высокой подвижности особей устойчивым может оказаться только тривиальное решение, если «подвижность» особей станет больше «критической».

Литература:

1.                   Александров А. Ю., Платонов А. В., Старков В. Н., Степенко Н. А. Математическое моделирование и исследование устойчивости биологических сообществ. СПб.: Соло, 2006. 186 с.

2.                   Базыкин А. Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: Институт компьютерных технологий, 2003. 368 с.

3.                   Бигон М., Харпер Дж., Таунсенд К. Экология. Особи, популяции и сообщества: в двух томах. М.: Мир, 1989. Т. 1. 667 с. Т. 2. 477с.

4.                   Вольтерра В. Математическая теория борьбы за существование. Москва-Ижевск:, Институт компьютерных технологий, 2004. 288 с.

5.                   Гилев А. В. Закономерности пространственного распределения и научные основы охраны рыжих лесных муравьев // Зоологический журнал. 2010. Т. 89. № 12. С. 1413–1420.

6.                   Глызин С. Д. Разностная аппроксимация уравнения «реакция — диффузия» на отрезке // Моделирование и анализ информационных систем. 2009. Т. 16. № 3. С. 96–116.

7.                   Годунов С. К., Рябенький В. С. Разностные схемы (введение в теорию). М.: Наука, 1973. 400 с.

8.                   Горбач В. В., Кабанен Д. Н. Пространственная организованность популяции черного аполлона (parnassius mnemosyne) в условиях Заонежья // Зоологический журнал. 2009. Т. 88. № 12. С. 1493–1505.

9.                   Горбунова Е. А., Колпак Е. П. Математические модели одиночной популяции // Вест. С.-Петерб. ун-та. Сер. 10. 2012. Вып. 4. С. 18–30.

10.               Громов В. С. Пространственно-этологическая структура популяций грызунов. М.: Т-во научн. изданий КМК. 2008. 581 с.

11.               Емельченко Н. Н. Обзор миграций белолобого гуся (anser albifrons) в Западной Палеарктике // Зоологический журнал. 2009. Т. 88. № 9. С. 1090–1108.

12.               Загребальный С. В., Фомин В. В., Бурдин А. М. Динамика численности, структуры популяции каланов Enhydra lutris на Командорских островах и оценка их миграционной активности между островами архипелага // Экология. 2008. № 1 С. 43–49.

13.               Зеленская Л. А. Численность и распределение птиц на острове Матыкиль (Ямские острова, Охотское море) // Зоологический журнал. 2009. Т. 88. № 5. С. 546–555

14.               Колпак Е. П., Горбунова Е. А., Балыкина Ю. Е., Гасратова Н. А. Математическая модель одиночной популяции на билокальном ареале // Молодой ученый. 2014. № 1 (6). С. 28–33.

15.               Коробченко М. А. Расширение ареала крота европейского (talpa europaea) в долине реки Северный Донец // Зоологический журнал. 2009. Т. 88. № 4. С. 465–472.

16.               Лидерман Г. В., Абатуров Б. Д., Быков А. В., Лопушков В. А. Динамика населения позвоночных животных Заволжской полупустыни. М.: Наука, 2005. 252 с.

17.               Мамонтов С. Н. Распределение по стволу дерева короеда-типографа (ips typographus, coleoptera, scolyniddae) и его энтомогафов // Зоологический журнал. 2009. Т. 88. № 9. С. 1139–1145.

18.               Мятлев В. Д., Панченко Л. А., Ризниченко Г. Ю., Терехин А. Т. Теория вероятностей и математическая статистика. Математические модели. М.: Издательский центр «Акадкмия», 2009. 320 с.

19.               Ризниченко Г. Ю., Рубин А. Б. Биофизическая динамика продукционных процессов. Москва — Ижевск: Институт компьютерных технологий, 2004. 464 с.

20.               Романов М. Ф., Федоров М. П. Математические модели в экологии. СПб.: Иван Федоров, 2003. 240 с.

21.               Садыков О. Ф., Бененсон И. Е. Динамика численности мелких млекопитающих: Концепции, гипотезы, модели. М.: Наука, 1992. 191с.

22.               Свирежев Ю. М. Нелинейные волны, диссипативные структуры и катастрофы в экологии. М: Наука, 1987. 368 с.

23.               Сейфулина Р. Р. Аранеокомплекс (arachnida, aranei) в агросистемах кубанской равнины (видовой состав, пространственное размещение и сезонная динамика) // Зоологический журнал. 2010. Т. 89. № 2. С. 151–166.

24.               Тихонов А. Н., Самарский А. А. Уравнение математической физики. М.: Наука, 1972. 735 с.

25.               Тютюнов Ю. В. Пространственная модель развития устойчивости насекомых-вредителей к трансгенной инсектицидной сельскохозяйственной культуре // Биофизика. Т. 52. № 1. С. 95–113.

26.               Шиятов С. Г., Терентьев М. М., Фомин В. В., Циммерман Н. Е. Вертикальный и горизонтальный сдвиги верхней границы редколесий и сомкнутых лесов в XX столетии на полярном Урале // Экология. 2007. № 4. С 243–248.

27.               McLeod P., Martin A. P., Richards K. J. Minimum length scale for growth — limited oceanic plankton distributions // Ecological Modeling. 2002. V. 158. № 1–2. P. 111–120.

28.               Mickens R. E. A nonstandard finite difference scheme for a PDE modeling combustion with nonlinear advection and diffusion // Mathematics and computers in simulation. 2005. № 69. P. 439–446.

29.               Mickens R. E. A nonstandard finite difference scheme for the diffusionless Burgers equation with logistic reaction // Mathematics and computers in simulation. 2003. № 62. P. 117–124.

30.               Murray D. D. Mathematical biology. N. Y. Springer. 2002. 551 p.

31.               Schofield P. Spatial explicit models of Turelli-Hoffmann Wolbachia invasive wave fronts // J. Theor. Biol. 2001. Vol. 212. N. 1. P. 121–131.