С каждым годом математические методы все больше проникают во все сферы жизни общества. Высокий уровень математической подготовки — необходимое условие успешности и востребованности выпускника на рынке труда. Работодатели ждут от молодых специалистов ответственности, способности логично мыслить, анализировать и прогнозировать результаты своей деятельности. И математика, как нельзя лучше, способствует формированию этих способностей. На занятиях, в процессе решения поставленных задач, у студентов формируется системность мышления и действий, способность к анализу, абстрагированию, систематизации.
Однако, зачастую, студенты задаются вопросом: зачем им математика, как она пригодится им в дальнейшей жизни, как знания формул и теорем помогут в выбранной специальности? Ответить на эти вопросы, а также показать студентам связь математики с их будущей профессией, изменить их эмоционально-чувственное отношение к предмету позволяют задачи прикладного характера.
Прикладные задачи — задачи из различных областей жизни, не связанных с математикой, но решаемые с помощью математических методов.
Прикладные агро-задачи — задачи и проблемы сельского хозяйства, решение которых осуществляется с помощью математики.
Прикладная агро-задача должна отвечать ряду требований:
1. Содержание задачи и ее решение должны демонстрировать прочную взаимосвязь между поставленной проблемой сельскохозяйственной практики и математическим аппаратом.
2. Способы решения должны быть направлены на применение теоретических знаний к проблемам сельского хозяйства.
3. Задача должна соответствовать целям и задачам курса высшей математики.
Например, тема «Производная и дифференциал» занимает одно из центральных в курсе высшей математики. Но ее изучение дается студентам с трудом. Для отработки использования табличных значений производных и правил дифференцирования, нахождения наибольшего и наименьшего значений, можно использовать следующие задачи:
1. Искусственный пруд для разведения карасей имеет форму прямоугольника, завершённого с двух сторон полукругом. Периметр пруда 80 метров. При каком радиусе полукруга, площадь пруда будет наибольшей?
2. Требуется соорудить клумбу и огородить ее декоративным забором. Периметр клумбы должен равняться 6м. Определить размеры клумбы, на забор для которой потребуется наименьшее количество материала.
3. Определить размеры резервуара для водопоя поросят с квадратным дном и объемом 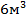 , чтобы на его сооружение пошло наименьшее количество материала.
, чтобы на его сооружение пошло наименьшее количество материала.
Решение каждой из данных задач подразумевает: анализ задачи, абстрагирование и запись условия на языке математики, нахождение производной, исследование на экстремум, переход от математических результатов к языку задачи.
Дифференциальные уравнения описывают многие физические и биологические процессы. Однако, традиционно, в рамках учебного процесса рассматриваются лишь основные виды дифференциальных уравнений и методы их решения. Не удивительно, что студенты не видят связи дифференциальных уравнений с задачами сельского хозяйства. В тоже время дифференциальные уравнения имеют широкое применение при моделировании биологических процессов. При изучении данной темы можно использовать задачи такого типа:
1. Составить дифференциальное уравнение изменения температуры тела и найти его решение.
В начальный момент (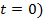 температура тела
температура тела 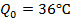 . Скорость изменения температуры характеризуется коэффициентом
. Скорость изменения температуры характеризуется коэффициентом 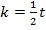 и температурой окружающей среды
и температурой окружающей среды 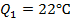 . Найти температуру тела в момент времени
. Найти температуру тела в момент времени 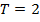 .
.
2. Составить дифференциальное уравнение, описывающее динамику прироста биомассы популяции кроликов и найти его решение. Известна начальная биомасса популяции 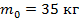 при
при 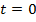 , скорость прироста биомассы кроликов пропорциональна биомассе популяции с коэффициентом
, скорость прироста биомассы кроликов пропорциональна биомассе популяции с коэффициентом 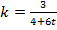 . Найти величину биомассы кроликов в момент времени
. Найти величину биомассы кроликов в момент времени 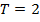 .
.
При составлении дифференциального уравнения, студенты вспоминают физический смысл производной (скорость изменения физических процессов) и применяют его к решению задачи. Получив дифференциальное уравнение, устанавливают его вид и способ решения. При нахождении общего решения дифференциального уравнения отрабатываются навыки интегрирования. Заканчивается решение интерпретацией полученных результатов.
Пытаясь выявить закономерности в наблюдаемом явлении, его характерные особенности, специалисту необходимо абстрагироваться от «помех», лишних, несущественных деталей. Перед ним стоит сложная задача разграничения случайных и неслучайных событий, систематизации зафиксированных данных, состоящих из огромного количества цифр. В решении данной задачи первостепенное значение имеют знания теории вероятностей и математической статистики. При изучении тем возможно использование следующих задач:
1. У фермера две коровы. Вероятность отела первой коровой составляет 0,6; второй — 0,9. Какова вероятность того, что: 1) отел будет у обеих коров; 2) отел будет хотя бы у одной коровы; 3) отел будет только у первой коровы.
Задача позволяет отработать формулу классической вероятности, операции над событиями, вероятности суммы и произведения, противоположного события.
2. Вероятность того, что масса холмогорского теленка при рождении окажется более 40 кг составляет 0,8. Составить ряд распределения числа телят с массой более 40кг из 4 новорожденных. Вычислить математическое ожидание и дисперсию. Найти вероятность, что из 4 телят не менее 3-х окажутся с массой более 40 кг.
3. Вероятность того, что масса яблока окажется более 160 г составляет 0,9. Составить ряд распределения числа яблок с весом более 160 г из 5 яблок. Вычислить математическое ожидание и дисперсию. Найти вероятность, что из 5 яблок не менее 3-х окажутся с весом более 160 г.
Анализ задачи позволяет выявить значения случайной величины. Соответствующие вероятности находятся по формуле Бернулли. Отрабатываются формулы нахождения числовых характеристик (математическое ожидание, дисперсия, среднее квадратическое отклонение), на основании предварительно составленного ряда распределения.
4. Вес поросят при рождении — случайная величина, распределенная по нормальному закону с математическим ожиданием 5 кг и средним квадратичным отклонением 1 кг. Какой процент новорожденных поросят имеет вес в пределах от 4,5 кг до 6 кг? Каков диапазон изменения веса поросят? Найти вероятность того, что отклонение веса поросят от стандартного значения, по абсолютной величине, составит не более 2 кг.
Формула Лапласа, правило «трех сигм» позволяют студентам ответить на вопросы задачи.
5. На уровне значимости 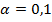 выяснить существенность влияния содержания катализатора на время химической реакции.
выяснить существенность влияния содержания катализатора на время химической реакции.
|
Содержание катализатора |
Повторности (номер эксперимента) |
|||
|
1 |
2 |
3 |
4 |
|
|
5 % |
5,5 |
5,9 |
6,5 |
6,0 |
|
10 % |
5,1 |
6,2 |
5,3 |
4,5 |
|
15 % |
6,8 |
7,5 |
8,2 |
8,0 |
6. Методом дисперсионного анализа исследовать зависимость привеса (г) поросят от содержания протеина в корме (г). Установить существенность влияния содержания протеина (фактора) при уровне значимости 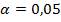 .
.
|
Протеин |
Повторности |
|||
|
1 |
2 |
3 |
4 |
|
|
80 |
520 |
530 |
550 |
540 |
|
90 |
550 |
570 |
580 |
570 |
|
100 |
610 |
620 |
590 |
580 |
Задачи дисперсионного анализа требуют от студентов особого внимания и точности расчетов. Они вызывают трудности арифметического характера, но вместе с тем приучают студентов к внимательности и ответственности. Решение сводится к нахождению и сравнению факторной и остаточной дисперсии, что позволяет оценить существенность влияния заданного условия на рассматриваемый признак.
Зачастую, проводимые измерения указывают на существование зависимости между величинами. Определяя тесноту этой зависимости, а так же как одна величина зависит от другой, оценивают степень корреляционной зависимости наблюдаемых случайных величин. Расчет коэффициентов корреляции и регрессии весьма трудоемок, так как требуется обработать большое количество исходных данных. Для отработки расчетных навыков у студентов используются задачи такого типа:
7. Методом корреляционного анализа исследовать зависимость между среднегодовым удоем молока от коровы 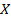 (ц) и расходом кормов на 1 корову в год
(ц) и расходом кормов на 1 корову в год 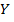 (ц. корм. ед.). Рассчитать коэффициенты регрессии и корреляции. Построить график корреляционной зависимости.
(ц. корм. ед.). Рассчитать коэффициенты регрессии и корреляции. Построить график корреляционной зависимости.
|
|
31,9 |
37,6 |
33,3 |
40,3 |
33,7 |
35,8 |
35,1 |
34,5 |
34,9 |
38,2 |
|
|
40 |
41 |
41 |
43 |
43 |
44 |
45 |
42 |
42 |
43 |
8. Методом корреляционного анализа исследовать зависимость между удельным весом картофеля 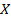 (
(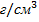 ) и содержанием крахмала
) и содержанием крахмала 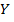 (%). Рассчитать коэффициенты регрессии и корреляции. Построить график корреляционной зависимости.
(%). Рассчитать коэффициенты регрессии и корреляции. Построить график корреляционной зависимости.
|
|
1,05 |
1,06 |
1,08 |
1,08 |
1,07 |
1,09 |
1,06 |
1,10 |
1,11 |
1,87 |
|
|
10 |
12 |
15 |
13 |
13 |
16 |
11 |
17 |
19 |
14 |
Биология, зоотехния, агрономия, агрохимия и другие направления сельского хозяйства с каждым годом все более математизируются. Эксперименты, проводимые специалистами, требуют значительных финансовых затрат. В связи с чем, требуют тщательного планирования, которое всегда опирается на анализ с использованием математического аппарата. Широко используются методы математического анализа, синтеза и абстрагирования, методы связанные с точными расчетами и сложными выкладками. В этой связи, изучение прикладных аспектов математики, решение задач прикладного характера, столь важно для студентов, будущих специалистов аграрного сектора.