Общая задача идентификации кинетических процессов формирования физико-механических характеристик композитов здесь решается, исходя из простоты и адекватности описания реальных кинетических процессов (с приемлемой для практических целей точностью и простотой физической интерпретации результатов).
Сравнение результатов экспериментальных исследований с теоретическими (дополнительная информация об искомом решении) показало возможность моделирования основных кинетических процессов(набор прочности, изменение модуля упругости, контракция и усадка, нарастание внутренних напряжений, тепловыделение, химическая стойкость, водопоглощение и водостойкость)вклассе обыкновенных дифференциальных уравнений n-го порядка. А именно, четвертогопорядка с постоянными коэффициентами и с действительными корнями характеристического полинома.
Опираясь на результаты многолетних исследований по синтезу материалов специального назначения [1…5], приведем основные модели для оценки формирования отдельных свойств материала (критериев качества).
Кинетическая модель набора прочности. Прочность композитов зависит от степени наполнения, дисперсности и физико-химической активности поверхности наполнителя, адгезионной связи в зоне контакта связующего и наполнителя, концентрации полимеризующего вещества, пористости композиции, температуры исходных компонентов, от технологии приготовления и некоторых других факторов. Регулирование прочности эпоксидных композитов возможно за счет использования комбинированных наполнителей, регулирования режимов отверждения, обработки аппретами, механической очистки поверхности наполнителя, введения модифицирующих, легирующих, пластифицирующих добавок, а также поверхностно активных веществ.
Кинетика набора прочности композитов часто аппроксимируется функцией
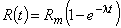 , (1)
, (1)
где 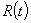 — прочность композита в момент времени t;
— прочность композита в момент времени t; 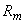 –максимальная прочность; t — время твердения; l — показатель, характеризующий скорость твердения (постоянный для данного материала).
–максимальная прочность; t — время твердения; l — показатель, характеризующий скорость твердения (постоянный для данного материала).
Легко показать, что (1) является частным случаем процесса
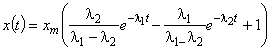 - (2)
- (2)
решение задачи Коши:
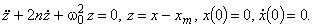 (3)
(3)
Таким образом, в обоих рассматриваемых случаях кинетический процесс набора прочности описывается динамической моделью вида (3).
Кинетика изменения модуля упругости. Другим из основных показателей свойств дисперсно-наполненных композитов является модуль упругости. Для его эффективного повышения особенно часто применяются дисперсные наполнители, хорошо смачивающиеся матричным связующим. Кинетическая модель изменения модуля упругости представляется в виде
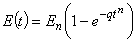 , (4)
, (4)
где n=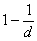 ; d — структурная размерность композиционной системы.
; d — структурная размерность композиционной системы.
Учитывая экспоненциальный характер кинетического процесса, и здесь вполне возможна ее аппроксимация линейной комбинацией функций вида 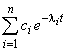 .
.
Кинетика контракции и усадки. Кинетика контракции и усадки является отражением процессов структурообразования. Структура композита (плотность, регулярность, упаковки, наличие или отсутствие дефектов, пористость) зависит не столько от величины энергии, сообщенной системе, сколько от скорости расхода этой энергии.
Кинетика контракции и усадки рассматриваемых материалов хорошо аппроксимируется в виде
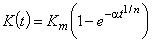 , (5)
, (5)
где К(t) — контракция в момент времени t; Кm — максимальная контракция для данного композита; a — коэффициент пропорциональности, характеризующий скорость отверждения, для полиэфирных смол n = 1.
И здесь наряду с (5) возможно описание кинетического процесса линейной комбинацией экспоненциальных функций вида 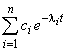 .
.
Кинетика нарастания внутренних напряжений. Внутренние напряжения связаны с неравномерно протекающими и незавершенными усадочными процессами. Знание механизма возникновения внутренних напряжений дает возможность направленно изменять их величину, например, путем уменьшения густоты пространственной сшивки полимера; увеличения гибкости макромолекул с увеличением за счет этого скорости релаксационных процессов; изменения характера надмолекулярных структур за счет влияния на скорость процессов структурообразования и т. д. Вид кинетических процессов нарастания внутренних напряжений приводится на рис. 1.
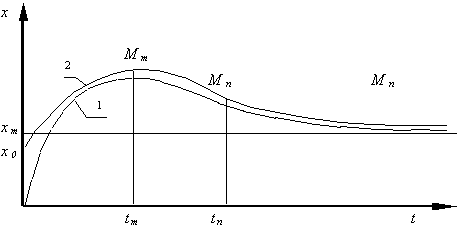
Рис. 1
Процессы вида, приведенные на рис.1, кривая 1, являются решением задачи Коши:
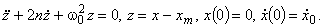 (6)
(6)
Процессы, приведенные на рис. 1, кривая 2, являются решением задачи Коши:
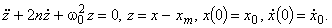 (7)
(7)
Процессы тепловыделения. Процесс образования структуры эпоксидного полимера происходит за счет присоединения к полимерной цепи каждого нового звена олигомера. Образование каждой новой связи в процессе полимеризации сопровождается выделением определенной порции тепла. Снижение тепловыделения при полимеризации является важным условием получения бездефектной структуры эпоксидного композита. Экспериментально определялась кинетика тепловыделения, которая имеет вид, аналогичный приведенному на рис.1, кривая 2. Указанные процессы являются решением задачи Коши (7).
Химическая стойкость композиций.Увеличение химической стойкости композита (стойкость материалов и конструкций в заданном интервале времени эксплуатации к воздействию агрессивных сред без разрушения и существенного изменения геометрических размеров и формы) достигается правильным выбором вяжущих и наполнителей (они должны иметь близкие значения коэффициента температурного расширения и упругих свойств, а также хорошую адгезию), созданием плотной структуры материала, а также введением в материал активных добавок. В рассматриваемом случае 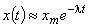 . Естественно сглаживание линейной комбинацией экспоненциальных функций даст более точные результаты. В частности, при n = 2 рассматриваемый кинетический процесс является решением задачи Коши:
. Естественно сглаживание линейной комбинацией экспоненциальных функций даст более точные результаты. В частности, при n = 2 рассматриваемый кинетический процесс является решением задачи Коши:
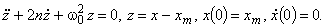 (8)
(8)
Здесь xm определяется непосредственно по экспериментально полученному процессу (xm = x(0)), параметр l легко определится методом наименьших квадратов.
Как следует из указанного выше, используемая экспоненциальная модель для анализа химической стойкости также является лишь частным случаем модели (7).
Водопоглощение и водостойкость. Вода оказывает разнообразное воздействие на композиционные строительные материалы; ускоряет процессы деструкции, изменяет свойства композитов. Поэтому сопротивление действию воды является одной из наиболее важных характеристик композиционного материала. Диффузия воды в композит во многом определяется проницаемостью граничного слоя полимер-наполнитель, которая в свою очередь и определяет водопоглощение и водостойкость композита. Например, водопоглощение и водостойкость эпоксидных композитов соответственно носят экспоненциально возрастающий и убывающий характер. Естественно, в соответствии с предыдущим более точно эти процессы могут описываться линейной комбинацией экспоненциальных функций. В частности, при n = 2они являются решением задачи Коши (8).
Моделирование процессов седиментации и флокуляции осуществляется на основе моделирования системы частиц (подробно рассматривалось в [5,7]).
Как показывает практика, существуют системы, кинетические процессы в которых не могут быть описаны рассмотренными выше моделями первого и второго порядка. К таким системам, в частности, относятся некоторые полидисперсные системы. Так, например, кинетика набора прочности композиционного материала имеет иногда не одну, а две точки перегиба. При этом на основе экспериментально полученных кинетических закономерностей формирования основных физико-механических характеристик композиционных материалов для их описания предлагается обобщенная динамическая модель [1]: кинетический процесс x(t) является решением задачи Коши:
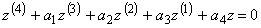 ,
,
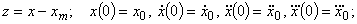
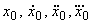 определяются требуемым видом кинетического процесса и заданным эксплуатационным значением
определяются требуемым видом кинетического процесса и заданным эксплуатационным значением 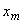 исследуемой характеристики материала.
исследуемой характеристики материала.
Таким образом, параметрическая идентификация и последующая оптимизация кинетических процессов сводится к определению параметров модели или связанных с ними корней характеристического полинома.
Литература:
1. Будылина Е. А., Гарькина И. А., Сухов Я. И. Математическое моделирование кинетических процессов в дисперсных системах / Молодой ученый. — 2013. — № 12. — С. 104–107.
2. Будылина Е. А., Гарькина И. А., Данилов А. М., Сухов Я. И. Некоторые подходы к анализу и синтезу сложных систем / Молодой ученый. — 2013. — № 10(57). — С.105–107.
3. Будылина Е. А., Гарькина И. А. Данилов А. М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. — 2013. –№ 2(16). — C. 138–143.
4. Гарькина И. А., Данилов А. М. Управление в сложных технических системах: методологические принципы проектирования системах / Региональная архитектура и строительство. — 2012. — № 1. — C. 39–42.
5. Данилов А. М., Гарькина И. А. Сложные системы: идентификация, синтез, управление: монография. — Пенза: ПГУАС. — 2011. –308 с.
6. Данилов А. М., Гарькина И. А. Методология проектирования сложных систем при разработке материалов специального назначения / Известия ВУЗов. Строительство.– 2011. — № 1. — С.80–85
7. Гарькина И. А., Данилов А. М., Смирнов В. А. Флокуляция в дисперсных системах /
8. Системы управления и информационные технологии. — 2008. — № 2.3 (32). — С. 344–346.







