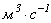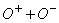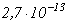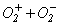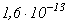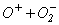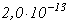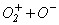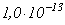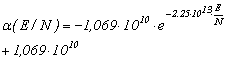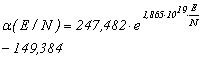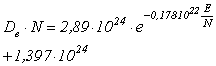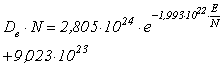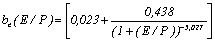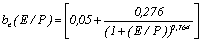В статье приводится система дифференциальных уравнений, моделирующая отрицательный коронный разряд, параметры модели принимаются функциями локальной напряженности электрического поля. На основе эмпирических данных получены аналитические зависимости коэффициентов ударной ионизации, диффузии и подвижности частиц от локальной напряженности. Проведен сравнительный анализ параметров модели для электроотрицательного и инертного газов, определено влияние свойств газа на значения коэффициентов.
Ключевые слова: коронный разряд, электроотрицательная корона, инертный газ, электроотрицательный газ, ударная ионизация, диффузия, подвижность.
1. Введение. Состав и свойства газов, заполняющих газоразрядный промежуток, оказывают существенное влияние на механизмы образования и закономерности протекания коронного разряда. Так, в электроотрицательных газах носителями заряда являются электроны и ионы обоих знаков, причем наличие отрицательных ионов обусловливает импульсный характер тока разряда (импульсы Тричеля). В инертных газах проводимость обеспечивают электроны и положительные ионы. В результате многочисленных экспериментальных исследований для различных газов были получены эмпирические зависимости параметров (коэффициенты ударной ионизации, прилипания, рекомбинации, диффузии, подвижности) от локальной напряженности электрического поля. Дж. Даттон [5] обобщил накопленные эмпирические данные, представив их в графической и табличной формах. Однако математическое моделирование коронного разряда сводится к решению системы дифференциальных уравнений, при этом удобнее использовать зависимости коэффициентов от локальной напряженности, представленные в виде функций. Таким образом, необходимо получить аналитический вид зависимостей и выявить закономерности изменения параметров модели в газах с различными свойствами.
2. Модель коронного разряда в электроотрицательном и инертном газах. Для моделирования коронного разряда в электроотрицательном газе (например, кислороде О2) применяется система дифференциальных уравнений второго порядка [1]:
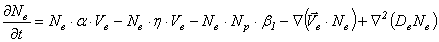 ;
;
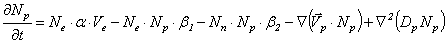 ;
;
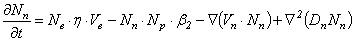 .
.
Данная система, решаемая совместно с уравнением Пуассона, позволяет определить концентрации электронов 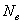 , положительных
, положительных 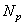 и отрицательных
и отрицательных 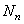 ионов и построить распределение частиц в газоразрядном промежутке. В качестве параметров модели выступают скорости частиц (
ионов и построить распределение частиц в газоразрядном промежутке. В качестве параметров модели выступают скорости частиц (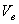 ,
, 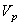 ,
, 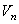 ), коэффициенты ионизации (
), коэффициенты ионизации (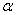 ), прилипания (
), прилипания (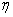 ), рекомбинации (
), рекомбинации (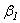 и
и 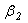 ) и диффузии (
) и диффузии (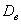 ,
,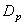 ,
,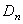 ). Предполагается, что параметры зависят от локальной напряженности поля (
). Предполагается, что параметры зависят от локальной напряженности поля (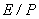 или
или 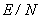 ) и не зависят от времени.
) и не зависят от времени.
Для инертного газа (например, аргона) из системы уравнений следует исключить всех слагаемые, содержащие параметры отрицательных ионов (концентрация 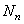 , коэффициенты прилипания
, коэффициенты прилипания 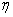 , ион-ионной рекомбинации
, ион-ионной рекомбинации 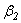 и диффузии
и диффузии 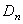 ). В результате получается система уравнений:
). В результате получается система уравнений:
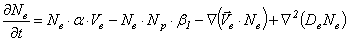 ;
;
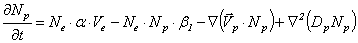 .
.
3. Сравнительный анализ зависимостей параметров моделей от локальной напряженности поля. Коэффициент ударной ионизации 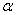 .Ударная ионизация – ионизация невозбужденных атомов (молекул) при столкновениях с электронами [2, с.22] – является основным механизмом рождения заряженных частиц в разрядном промежутке. На рис. 1 а представлен график зависимости коэффициента ударной ионизации от локальной напряженности электрического поля для кислорода, построенный на основе экспериментальных данных D. Price [5]. На рис. 1 б – график той же зависимости для аргона, построенный на основе экспериментов A. Kruithof [5]. Аппроксимация проводилась в математическом пакете MATHCAD.
.Ударная ионизация – ионизация невозбужденных атомов (молекул) при столкновениях с электронами [2, с.22] – является основным механизмом рождения заряженных частиц в разрядном промежутке. На рис. 1 а представлен график зависимости коэффициента ударной ионизации от локальной напряженности электрического поля для кислорода, построенный на основе экспериментальных данных D. Price [5]. На рис. 1 б – график той же зависимости для аргона, построенный на основе экспериментов A. Kruithof [5]. Аппроксимация проводилась в математическом пакете MATHCAD.
В результате были получены аналитические зависимости для кислорода:
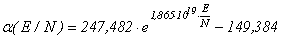 ,
,
для аргона:
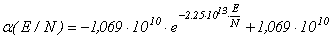 .
.
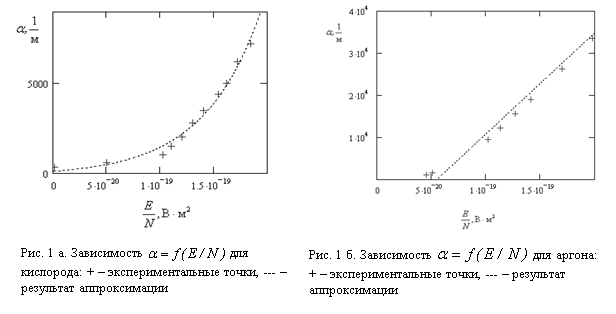 Из полученных зависимостей видно, что значения коэффициента ударной ионизации для аргона на порядок выше, чем для кислорода. Так, при значении локальной напряженности
Из полученных зависимостей видно, что значения коэффициента ударной ионизации для аргона на порядок выше, чем для кислорода. Так, при значении локальной напряженности 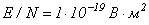 для кислорода
для кислорода 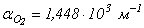 , для аргона
, для аргона 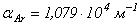 . Данный факт хорошо согласуется со значениями пробивного напряжения: для аргона
. Данный факт хорошо согласуется со значениями пробивного напряжения: для аргона 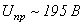 , что существенно ниже, чем для двух и многоатомных газов (
, что существенно ниже, чем для двух и многоатомных газов ( 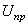 от 280 В до 420 В)[3, c. 108]. Кроме того, из рис. 1 видно, что с ростом локальной напряженности коэффициент ударной ионизации для аргона увеличивается быстрее, чем для кислорода, поэтому график зависимости
от 280 В до 420 В)[3, c. 108]. Кроме того, из рис. 1 видно, что с ростом локальной напряженности коэффициент ударной ионизации для аргона увеличивается быстрее, чем для кислорода, поэтому график зависимости 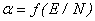 для аргона в заданном интервале напряженностей близок к прямой линии.
для аргона в заданном интервале напряженностей близок к прямой линии.
Коэффициенты электрон-ионной и ион-ионной рекомбинации.Электрон-ионная рекомбинация является процессом, обратным ударной ионизации и приводит к уменьшению количества заряженных частиц в газоразрядном промежутке. Экспериментальные исследования Ю.П. Райзера [4] и Дж. Даттона [5] показали, что коэффициент рекомбинации существенно зависит от температуры и практически не зависит от локальной напряженности поля. Для аргона, в соответствии с результатами экспериментов F.J. Mehr [5], при температуре 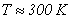 коэффициент рекомбинации электронов и положительных ионов принимает значение
коэффициент рекомбинации электронов и положительных ионов принимает значение 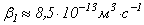 и уменьшается по мере увеличения температуры газа. Для кислорода по результатам экспериментов W.H. Kasner и D. Smith [5]
и уменьшается по мере увеличения температуры газа. Для кислорода по результатам экспериментов W.H. Kasner и D. Smith [5] 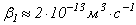 . Ион-ионная рекомбинация наблюдается только в электроотрицательных газах. В таблице 1 приведены возможные варианты ион-ионной рекомбинации в кислороде и значения соответствующих коэффициентов
. Ион-ионная рекомбинация наблюдается только в электроотрицательных газах. В таблице 1 приведены возможные варианты ион-ионной рекомбинации в кислороде и значения соответствующих коэффициентов 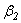 [4, с.79].
[4, с.79].
Таблица 1
Ион-ионная рекомбинация в кислороде
|
Рекомбинирующие ионы |
Значение коэффициента рекомбинации |
|
|
|
|
|
|
|
|
|
|
|
|
 Коэффициенты диффузии электронов и ионов. Диффузия заряженных частиц играет большую роль в возникновении газового разряда, в частности, объясняет импульсный характер коронного разряда в электроотрицательном газе. На рис. 2 а представлен график зависимости произведения коэффициента диффузии электронов и концентрации частиц от локальной напряженности поля (
Коэффициенты диффузии электронов и ионов. Диффузия заряженных частиц играет большую роль в возникновении газового разряда, в частности, объясняет импульсный характер коронного разряда в электроотрицательном газе. На рис. 2 а представлен график зависимости произведения коэффициента диффузии электронов и концентрации частиц от локальной напряженности поля (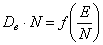 ) для кислорода, построенный на основе экспериментальных данных D. Nelson [2], на рис. 2 б – аналогичный график для аргона по результатам экспериментов Wagner [5].
) для кислорода, построенный на основе экспериментальных данных D. Nelson [2], на рис. 2 б – аналогичный график для аргона по результатам экспериментов Wagner [5].
В результате была получена аналитическая функция для кислорода:
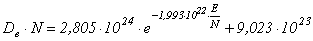 ;
;
для аргона:
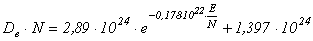 .
.
Из полученных функциональных зависимостей видно, что коэффициенты диффузии для кислорода и аргона существенно отличает только степень экспоненты: для кислорода она на порядок больше, чем для аргона. Поэтому с ростом локальной напряженности произведение коэффициента диффузии на концентрацию частиц для кислорода снижается быстрее, чем для аргона (рис. 2).
Для определения коэффициентов диффузии положительных 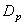 и отрицательных
и отрицательных 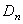 ионов применяется соотношение Эйнштейна, связывающее их с подвижностями:
ионов применяется соотношение Эйнштейна, связывающее их с подвижностями:
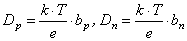 ,
,
где 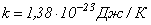 – постоянная Больцмана,
– постоянная Больцмана, 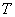 – температура газового разряда,
– температура газового разряда, 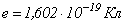 – элементарный заряд.
– элементарный заряд.
 Скорости (подвижности) частиц.Скорости частиц связаны с их подвижностями
Скорости (подвижности) частиц.Скорости частиц связаны с их подвижностями 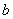 (
(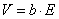 ), поэтому интерес представляет исследование зависимости подвижности частиц от локальной напряженности
), поэтому интерес представляет исследование зависимости подвижности частиц от локальной напряженности 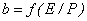 . Зависимость скорости электронов
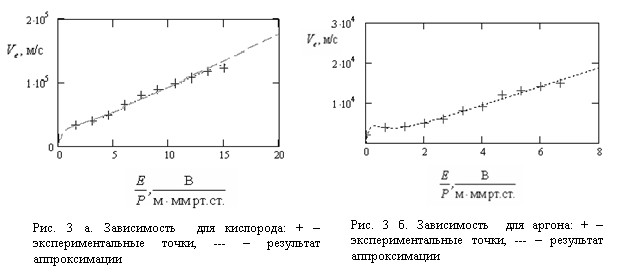
. Зависимость скорости электронов 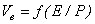 для различных газов приведена в работе Ю.П. Райзера [4, с. 42]. На рис. 3 а представлен график
для различных газов приведена в работе Ю.П. Райзера [4, с. 42]. На рис. 3 а представлен график 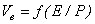 для кислорода, на рис. 3 б – для аргона, полученные по результатам исследований С. Брауна [5].
для кислорода, на рис. 3 б – для аргона, полученные по результатам исследований С. Брауна [5].
В результате аппроксимации была получена функциональная зависимость подвижности электронов от локальной напряженности для кислорода:
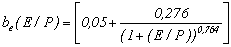 ;
;
для аргона:
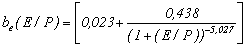 .
.
Функции существенно отличает степень знаменателя дроби (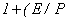 )), что сказывается на внешнем виде графиков (рис. 3). Расчеты показывают, что с ростом напряженности электрического поля подвижность электронов стремится к постоянной величине. Для кислорода при больших локальных напряженностях
)), что сказывается на внешнем виде графиков (рис. 3). Расчеты показывают, что с ростом напряженности электрического поля подвижность электронов стремится к постоянной величине. Для кислорода при больших локальных напряженностях 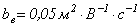 , для аргона
, для аргона 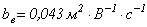 , что согласуется с результатами экспериментов [6].
, что согласуется с результатами экспериментов [6].
Подвижности ионов в газоразрядном промежутке определяют по формуле Ланжевена [4, с. 55]. Расчеты позволяют получить следующие значения: для положительных и отрицательных ионов кислорода при 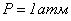
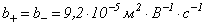 , для аргона
, для аргона 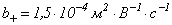 .
.
4. Вывод. Для параметров модели отрицательного коронного разряда в кислороде и аргоне на основе эмпирических данных нами были получены аналитические зависимости, сведенные в таблицу 2.
Таблица 2
Эмпирические зависимости параметров модели для аргона и кислорода
|
Коэффициенты |
Аргон |
Кислород |
|
Ударной ионизации |
|
|
|
Электрон-ионной рекомбинации |
|
|
|
Диффузии электронов |
|
|
|
Подвижность электронов |
|
|
|
Подвижность ионов |
|
|
Как видно из результатов математической обработки экспериментальных данных существенное расхождение наблюдается только для коэффициента ударной ионизации (у аргона он на порядок выше, чем у кислорода). Остальные параметры можно считать достаточно близкими (по порядку величины) и при рассмотрении коронного разряда в первичном приближении различия в их значениях не учитывать. Однако детальное изучение закономерностей протекания коронного разряда потребует получения более точных аналитических зависимостей для широкого интервала значений локальной напряженности поля.
Литература:
1. Брант ван Р. Физика и химия частичных разрядов и короны: последние достижения и будущие последствия: Уайтхедовские чтения. 1994. URL: http://sibdiag.ru.
2. Капцов Н. А. Электрические явления в газах и вакууме. М.: Гос. изд-во технико-технической литературы, 1950. – 836 с.
3. Колесов С.Н., Колесов И.С. Материаловедение и технология конструкционных материалов. – М.: Высшая школа, 2004. – 519 с.
4. Райзер Ю. П. Физика газового разряда. М.: Наука, 1992 – 536 с.
5. Dutton J. A Survey of Electron Swarm Data // J. Phys. Chem. Ref. Data. 1975. Vol. 4, №3. Р. 577-856. URL: http://www.nist.gov/data/PDFfiles/jpcrd69.pdf.
6. Sattari P., Adamiak K. Numerical Simulation of Trichel Pulses in a Negative Corona Discharge in Air // IEEE. Transactions on Industry Applications. 2010. Vol. 47. P. 1935-1943.