имени А. П. Чехова (Ростовская обл.)
Текстовые задачи в математическом образовании младших школьников играют огромную роль. Умение решать задачи является одним из основных показателей уровня математического развития школьника, глубины освоения им учебного материала. Поэтому перед учителем начальной школы стоит главная задача — научить учащихся решать арифметические задачи [6, с. 94], в том числе, задачи на движение. Решение этого типа задач связано с использованием таких понятий, как абстракция, аналогия, гипотеза и др. Моделирование рассматривается как основной метод обучения. Главная особенность метода моделирования состоит в том, что это метод опосредованного познания предмета с помощью объектов-заместителей. Модель выступает и используется в процессе обучения как своеобразный инструмент познания, с помощью которого исследуется и изучаетсятот или иной объект, который изучается посредством его моделирования. Модель определяется нами как некий объект (система), исследование которого служит средством получения новых знаний о другом объекте (оригинале). Проектирование в школе современных, так называемых, проблемных методов обучения имитируется как процесс обучения, так и как путь научного познания. Поэтому моделирование в школе может использоваться как вид проектирования учебной деятельности, и как прием обучения в разных методических системах. Когда учитель ставит цель наглядно показать учащимся движение тел в противоположном направлении, он использует модель — заместитель реальной ситуации, чертеж отрезка прямой линии, по которой движутся тела, и направление их движения. В этом случае совершенно очевидно моделирование используется как вид проектирования учебной деятельности учащихся. Когда учитель говорит: «Представим себе (предположим).».., то моделирование используется как способ познания, при котором имеются:
1) субъект познания (учащиеся);
2) объект познания (ситуация, отраженная в тексте задачи);
3) модель, опосредствующая отношения познающего субъекта и познаваемого объекта.
Таким образом, поскольку моделирование служит способом, а модель средством познания, то учитель, таким образом, проектирует учебную деятельность младших школьников, а учащиеся под руководством учителя пользуются и тем и другим в процессе получения новых знаний. Это означает, что моделирование может успешно применяться и как вид проектирования учебной деятельности, и как способ алгоритмизации учебной деятельности учащихся.
Мы будем рассматривать такие «модели», которые являются инструментами получения новых знаний. Разграничивая моделирование процесса познания и моделирование задачи как таковой, под моделированием (проектированием) учебной деятельности в процессе познания понимаем построение, изучение и применение моделей в процессе обучения решению текстовых задач [5, с. 17].
Существующие программы обучения математике, учебники «Математика» для начальной школы содержат такой вид знаково-символической деятельности, как кодирование, схематизация, моделирование. Программой так же предусмотрена выработка умений учащихся отобразить некоторое явление, свойство по определенным правилам, умений сделать схему, чертеж и, наконец, умения моделировать в процессе решения разного рода математических задач, то есть переводить ситуацию, отраженную в задаче, на язык математических символов, схем, графических чертежей, арифметических действий.
Обучая решению задач на движение, учитель демонстрирует сначала готовые модели; постепенно под руководством учителя учащиеся переходят к построению разного рода моделей (овладевают приемами моделирования). Такие действия учителя являются приемом проектирования учебной деятельности учащихся, используя для этой цели модель как способ познания.
Подготовка учащихся к решению задач на движение с использованием приема моделирования начинается во втором классе. Сначала демонстрируются готовые модели, отражающие виды движения. Решая задачу: «Длина аллеи 70 м. Два мальчика одновременно пошли навстречу друг другу с разных концов аллеи. Один прошел до встречи 22 м. Сколько метров прошел до встречи другой мальчик?», учащиеся по рисунку учебника [1, с. 53] производят:
- анализ данной модели (рис. 1);

Рис. 1.
- выделяют смысловые части системы элементов данных в задаче и их отношений, которые изображены с помощью знаково-символических средств;
- приходят к выводу, что мальчики: 1) вышли из разных пунктов и идут навстречу друг другу; 2) один мальчик прошел до места встречи 22 м (другой — до момента встречи прошел большее расстояние, чем первый. Это визуально определяется по чертежу); 3) расстояние между пунктами 70 м; 4) требуется определить, какое расстояние, прошел второй мальчик.
Прием моделирования учебной деятельности учащихся продолжается как процесс подготовки к решению задач на движение постепенным усложнением решаемых задач. В учебнике «Математика», 2 класс читаем: Составьте по схематическому чертежу задачу и реши ее.

Рис. 2.
Анализируя чертеж (рис. 2), учащиеся, используя модель как процесс познания, определяют, что: 1) девочка догоняет мальчика (очевидно по рисунку). Учащиеся осознают, что осуществляется движение в одном направлении; 2) дети выбежали из одного пункта; 3) мальчик бежит быстрее, чем девочка — он оказался впереди девочки (получают представление о скорости движения); 4) расстояние, пройденное мальчиком (зафиксировано) составляет 100 м, а девочке нужно пробежать еще 30м (видят расстояние, уже пройденное мальчиком, и расстояние, которое осталось пройти девочке до места назначения); 5) нужно найти расстояние, которое прошла девочка на момент остановки мальчика (это расстояние отмечено знаком «?»).
Хотя обучение решению задач на движение в соответствии с государственными стандартами школ России предусмотрено в четвертом классе, тем не менее в учебнике «Математика», 2 класс, часть 2 дается представление и о таком виде движения как движение навстречу друг другу [2, с. 37].
По модели движения и по данным задачи учащиеся должны составить задачу и решить ее (рис. 3), затем составить две задачи, обратные первой, и решить их.

Рис. 3.
Для составления обратной задачи учащиеся должны не только изменить модель, но и соотнести вновь полученные модели с реальностью, что позволит им получить новую информацию о моделируемой задаче, глубже проникнуть в ее суть.
Обучение приему моделирования, как методу познания, продолжается в 3 классе [3, с. 3]. Рассмотрим задачу: «Нина и Коля, когда идут из дому в школу, подходят к зданию школы с разных сторон. От Нининого дома до здания школы 40 м, а от Колиного — 60 м. Узнайте расстояние между этими домами».
1) Сделайте чертеж к задаче и решите ее.
2) Сравните свой чертеж и решение с теми чертежами, которые выполнили девочки:
Оля сделала такой чертеж (рис. 4):
 Рис. 4.
Рис. 4.
Решение: 40 + 60 = 100 (м). Ответ: 100 метров.
Вера сделала такой чертеж (рис. 5):
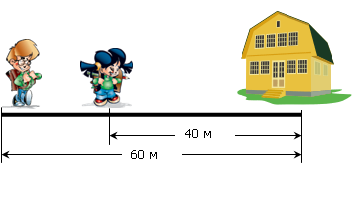
Рис. 5.
Решение: 60–40 = 20 (м). Ответ: 20 метров.
3) Какой из чертежей отражает (моделирует) условие задачи? Как нужно изменить условие задачи (какие слова надо добавить в условие), чтобы права была Оля, и как — чтобы права была Вера. Или: какую задачу можно составить по Олиному чертежу, а какую — по чертежу Веры.
Анализируя условие, соответствующие чертежи и решения задач, учащиеся не только соотносят модель с реальными ситуациями, но и проникают в суть пространственных отношений, выражаемых словами: «находится между …», «находится по разные стороны от…», «находится по одну сторону от …» и др.
Значительное место использованию приема моделирования в процессе познания уделяется в четвертом классе. Так, подготовкой к решению задач на движение методом моделирования являются задачи типа: «Из двух городов навстречу друг другу вышли две машины. Одна из них до встречи с другой прошла 128 км, другая — на 56 км меньше. Сделайте чертеж к задаче и узнайте расстояние между городами» [4, с. 83].
Для рационального решения задач такого вида учащиеся должны смоделировать текст задачи. Это значит, что необходимо показать: 1) направление движения; 2) соответственно условию отметить расстояние, пройденное одной машиной до встречи с другой; 3) соотнести его с расстоянием, пройденным другой машиной («на меньше»); 4) указать соответственно пройденному расстоянию каждой машиной место встречи.
Покажем как учитель проектирует учебную деятельность учащихся при работе с задачей: «Расстояние между остановками автобусов 1 км. От остановок отошли 2 автобуса, но в пути они остановились. Один из них до момента остановки проехал 140 м, другой — 160 м. На каком расстоянии друг от друга остановились автобусы?» [4, с.41] (рис. 6 и 7).
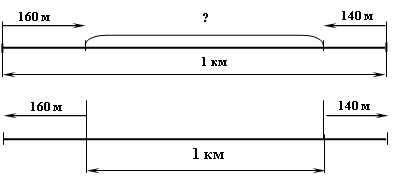
Рис. 6 и 7
Возможно при этом выполнение заданий типа:
− Сформулируйте недостающее условие и (или: − Чего не хватает в задаче для ее решения?).
Учитель предлагает учащимся рассмотреть два чертежа (рис. 6 и 7) с изображенными на них моделями движения.
Далее разбор задачи идет в зависимости от уровня развития учащихся, от скорости их мышления, от способности к аналитическому мышлению, от способности к догадке и т. д. Главное, чтобы учащиеся при одинаковых числовых значениях исходных величин, при одном и том же вопросе обнаружили различие одного из элементов модели: в первом случае автомобили двигались навстречу в противоположных направлениях, сближаясь друг с другом (рис. 6), во втором двигались в противоположных направлениях (рис. 7) — удаляясь друг от друга.
Соответственно этими выражениями учащиеся дополняют условия «двигались навстречу, сближаясь», «двигались, удаляясь друг от друга». При этом учитель обращает внимание на то, что в обоих случаях автобусы двигались в противоположных направлениях, но в одном случае — сближались, в другом — удалялись друг от друга. И на вопрос учителя, сколько задач изображено на рисунках, учащиеся ответят: «Две задачи».
Возможен иной вариант проектирования учебной деятельности: учащимся дается задание по двум отраженным в моделях видам движений объектов относительно друг друга (рис. 6 и рис. 7) придумать вопрос задачи.
Учащиеся сравнивают модели и при одинаковых обозначенных на двух рисунках числовых значениях исходных данных формулируют один и тот же вопрос: «Каким было расстояние между автобусами в момент их остановки?» (или: − На каком расстоянии автобусы остановились друг от друга?).
Уместным может оказаться вопрос, который может быть задан до или после предыдущего: − Когда автобусы остановились в пути, в каком случае (предложенном на 6-м или 7-м рисунке) расстояние между автобусами было больше, и в каком, соответственно, меньше?
Этот вопрос будет способствовать уяснению важнейшего элемента модели, без которого задачи данного типа не существует, а именно: движутся ли объекты при движении в разных (противоположных) направлениях, навстречу друг другу, сближаясь (когда расстояние между ними уменьшается), или в разные стороны, удаляясь друг от друга (когда расстояние между ними увеличивается). В зависимости от этого элемента, в котором отражен разный характер взаимно направленного движения в противоположных направлениях, на один и тот же вопрос: − На каком расстоянии друг от друга остановились автобусы (или: − Каково (чему равно) расстояние между автобусами в момент их остановки в пути?) будут получены разные ответы, как и принципиально разными будут решения этих двух задач.
В соответствии с моделью движения, отраженной на рисунке 6, имеем решение:
1. 160 + 140 = 300 (м) — проехали автобусы до остановки.
2. 1000–300 = 700 (м) — между автобусами на момент остановки.
В соответствии с моделью движения, отраженной на рисунке 7, имеем решение:
160 + 140 + 1000 = 1300 (м) — расстояние между автобусами на момент остановки.
Подобные задания, а их в учебнике немало, способствуют приему моделирования как процессу познания при решении задач на движение. Учитель, направляя деятельность учащихся, способствует тому, чтобы в рассмотренных ситуациях учащиеся выделили те компоненты задачи, которые необходимы им для ее решения, осуществляя тем самым процесс абстрагирования.
Понятная и усвоенная учениками модель задачи вызывает у них наглядный образ существенных свойств моделируемого объекта, то есть дает возможность ученикам выделить такие существенные свойства движении, как: «двигаться навстречу друг другу», «двигаться в противоположных направлениях навстречу друг другу», «двигаться в противоположных направлениях в разные стороны, удаляясь друг от друга». Все остальные свойства, несущественные в данном случае, отбрасываются. Таким образом, у учащихся создается обобщенный образ моделируемого объекта.
Итак, моделирование в обучении математике служит методическим приемом, а именно приемом проектирования учебной деятельности учащихся, приемом формирования у учащихся математических понятий, приемом привития им навыков математических действий, а также использования моделей как внешних опор для организации мыслительной деятельности.
Литература:
1. Моро М. И., Бантова М. А., Бельтюкова Г. В., Волкова С. И., Степанова С. В. Математика. 2 класс. Ч. 1. − М., 2011.
2. Моро М. И., Бантова М. А., Бельтюкова Г. В., Волкова С. И., Степанова С. В. Математика. 2 класс. Ч. 2. − М., 2011.
3. Моро М. И., Бантова М. А., Бельтюкова Г. В., Волкова С. И., Степанова С. В. Математика. 3 класс. Ч. 1. − М., 2011.
4. Моро М. И., Бантова А. М., Бельтюкова Г. В., Волкова С. И., Степанова С. В. Математика. 4 класс. Ч. 1. − М., 2011.
5. Тихоненко А. В. Обучение решению текстовых задач в начальной школе. — Ростов-на/Д, 2007.
6. Трофименко Ю. В. Типовые текстовые задачи, рассматриваемые в курсе математики на факультете педагогики и методики начального образования. Вестник Таганрогского государственного педагогического института. 2013. № 1.







