Известно, что трубопроводом называется устройство, предназначенное для транспортировки жидких, газообразных или сыпучих сред. Классификация трубопроводов достаточно обширна, но все трубопроводы в первую очередь делятся на магистральные, городские коммунально-сетевые и техно-экологические. В свою очередь каждый из перечисленных видов трубопроводов имеет свою классификацию, которая более подробно представлена, например, в [1]. В зависимости от транспортируемой среды применяются различные термины для конкретизации названия трубопровода: водопровод, газопровод, нефтепровод и др. Каждому трубопроводу предъявляются определенные требования по их прочности, безопасности, непроницаемости, долговечности и т.п.
Одной из важнейших задач практического использования трубопроводов является
повышение их прочности. Важными составляющими при исследовании прочности трубопровода является использование соответствующего материала изделия и размеры поперечного сечения. Проведение расчета элемента трубопровода на прочность позволит, в частности, обоснованно выбрать наиболее приемлемый материал, из которого будет произведен трубопровод, подобрать оптимальные размеры поперечного сечения.
Рассмотрим трубопровод как толстостенный цилиндр (рис. 1). Для определенности вводим обозначения: 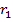 – внутренний радиус,
– внутренний радиус, 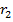 – внешний радиус, t– толщина трубы.
– внешний радиус, t– толщина трубы.
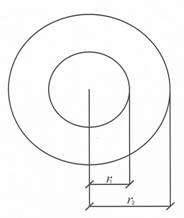
Рис. 1. Поперечное сечение трубопровода
В теории расчета толстостенных цилиндров доказано, что при действии внутреннего и внешнего давлений возникают нормальные напряжения на цилиндрической поверхности элемента, имеющего радиус r, которые принято обозначать 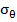 . Также возникают нормальные напряжения на плоских гранях элемента, которые обозначают
. Также возникают нормальные напряжения на плоских гранях элемента, которые обозначают 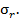 Будем придерживаться общепринятой терминологии:
Будем придерживаться общепринятой терминологии: 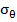 – тангенциальные, или окружные напряжения;
– тангенциальные, или окружные напряжения; 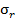 – радиальные напряжения.
– радиальные напряжения.
Рассмотрим трубопровод под действием внутреннего давления p. На основании общих формул вычисления нормальных напряжений 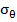 и
и 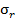 , приведенных, в частности, в [2, с.475], получим формулы вычисления радиальных и окружных напряжений в нашем частном случае
, приведенных, в частности, в [2, с.475], получим формулы вычисления радиальных и окружных напряжений в нашем частном случае
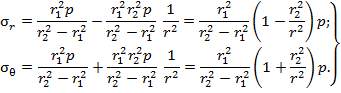
Введем коэффициент 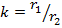 , который назовем коэффициентом формы. Так как по условию приняли
, который назовем коэффициентом формы. Так как по условию приняли 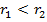 , то теоретически этот коэффициент должен изменяться в интервале от 0 до 1:
, то теоретически этот коэффициент должен изменяться в интервале от 0 до 1: 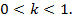 Дополнительно относительно интервала изменения коэффициента
Дополнительно относительно интервала изменения коэффициента 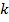 можно сделать следующее замечание. Принято цилиндр считать толстостенным, если выполняется соответствующее условие для толщины его стенки [2, с. 471], именно:
можно сделать следующее замечание. Принято цилиндр считать толстостенным, если выполняется соответствующее условие для толщины его стенки [2, с. 471], именно:
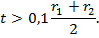
Следовательно, для толщины трубопровода также должно выполняться это условие
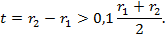
Решая записанное неравенство с учетом величины введенного коэффициента 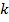 , получим, что существует ограничение этого коэффициента:
, получим, что существует ограничение этого коэффициента: 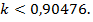 Поэтому можно принять интервал изменения для
Поэтому можно принять интервал изменения для 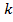 в виде
в виде 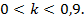 С учетом принятых обозначений радиусов очевидно, что чем меньше значение коэффициента формы, тем меньше внутренний радиус, то есть меньше внутреннее пространство и, соответственно, толще стенки трубопровода. С увеличением значения коэффициента формы
С учетом принятых обозначений радиусов очевидно, что чем меньше значение коэффициента формы, тем меньше внутренний радиус, то есть меньше внутреннее пространство и, соответственно, толще стенки трубопровода. С увеличением значения коэффициента формы 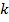 увеличивается внутреннее пространство, уменьшается толщина стенки трубопровода. Для практического использования изделия именно в виде трубопровода необходимо иметь достаточное внутреннее пространство, следовательно, окончательно принимаем интервал изменения коэффициента формы в виде
увеличивается внутреннее пространство, уменьшается толщина стенки трубопровода. Для практического использования изделия именно в виде трубопровода необходимо иметь достаточное внутреннее пространство, следовательно, окончательно принимаем интервал изменения коэффициента формы в виде 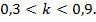 Таким образом, нижний предел изменения коэффициента
Таким образом, нижний предел изменения коэффициента 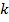 заведомо принимаем несколько большим, чем это допустимо теоретически.
заведомо принимаем несколько большим, чем это допустимо теоретически.
С учетом зависимости 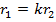 представленные ранее формулы радиальных и тангенциальных нормальных напряжений принимают вид
представленные ранее формулы радиальных и тангенциальных нормальных напряжений принимают вид
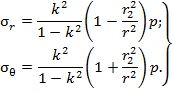
Здесь r – произвольный радиус элемента поверхности трубопровода, для которого вычисляются нормальные напряжения.
Очевидно, при 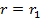 получим значения напряжений на внутренней поверхности трубопровода в виде
получим значения напряжений на внутренней поверхности трубопровода в виде
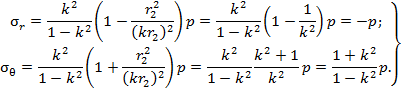
Современные трубопроводы широко представлены в виде металлических и пластиковых труб, имеющих различные свойства, область применения, способы монтажа и срок эксплуатации. Для выполнения расчетов в качестве материалов трубопроводов приняты сталь, отожженная медь, поливинилхлорид (ПВХ), полиэтилен высокого давления (ПВД). Именно эти материалы в настоящее время получили наибольшее распространение для трубопроводов промышленного и бытового назначения. На основании существующих СНиП для трубопроводов [1] и с учетом результатов испытаний, представленных в [3] для каждого из вариантов выполненных расчетов напряжений принимаем внутренне давление трубопровода 12,5 МПа. При постоянном значении внутреннего давления и задаваемом значении коэффициента формы вычислены нормальные радиальные 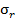 и окружные напряжения
и окружные напряжения 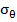 , а также эквивалентное напряжение
, а также эквивалентное напряжение 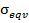 . При вычислении эквивалентного напряжения использована третья теория прочности. Варианты расчетов, выполненных с помощью программного комплекса Excel, приведены в таблицах 1–3.
. При вычислении эквивалентного напряжения использована третья теория прочности. Варианты расчетов, выполненных с помощью программного комплекса Excel, приведены в таблицах 1–3.
На рис. 2 представлены графики, построенные на основе расчетных значений, приведенных в таблице. Построение графиков также выполнено в Excel. По оси ординат отложены значения расчетных сопротивлений исследуемых и возможных материалов трубопроводов. По оси абсцисс отложены значения долей толщины трубопровода. Расчеты
Таблица 1. Расчетные значения напряжений при 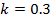
|
Нагрузка, МПа |
Доля толщины |
|
|
|
|
12,500 |
0,700 |
0,000 |
2,473 |
2,473 |
|
12,500 |
0,600 |
-0,290 |
2,763 |
3,053 |
|
12,500 |
0,550 |
-0,475 |
2,947 |
3,422 |
|
12,500 |
0,500 |
-0,695 |
3,168 |
3,863 |
|
12,500 |
0,400 |
-1,287 |
3,759 |
5,046 |
|
12,500 |
0,350 |
-1,690 |
4,162 |
5,852 |
|
12,500 |
0,300 |
-2,198 |
4,670 |
6,868 |
|
12,500 |
0,200 |
-3,709 |
6,181 |
9,890 |
|
12,500 |
0,100 |
-6,490 |
8,963 |
15,453 |
|
12,500 |
0,000 |
-12,500 |
14,973 |
27,473 |
Таблица 2. Расчетные значения напряжений при 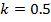
|
Нагрузка, МПа |
Доля толщины |
|
|
|
|
12,500 |
0,500 |
0,000 |
8,333 |
8,333 |
|
12,500 |
0,450 |
-0,450 |
8,783 |
9,234 |
|
12,500 |
0,400 |
-0,977 |
9,311 |
10,288 |
|
12,500 |
0,350 |
-1,600 |
9,934 |
11,534 |
|
12,500 |
0,300 |
-2,344 |
10,677 |
13,021 |
|
12,500 |
0,250 |
-3,241 |
11,574 |
14,815 |
|
12,500 |
0,200 |
-4,337 |
12,670 |
17,007 |
|
12,500 |
0,150 |
-5,695 |
14,029 |
19,724 |
|
12,500 |
0,100 |
-7,407 |
15,741 |
23,148 |
|
12,500 |
0,000 |
-12,500 |
20,833 |
33,333 |
Таблица 3. Расчетные значения напряжений при 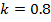
|
Нагрузка, МПа |
Доля толщины |
|
|
|
|
12,500 |
0,200 |
0,000 |
44,444 |
44,444 |
|
12,500 |
0,190 |
-0,451 |
44,896 |
45,347 |
|
12,500 |
0,180 |
-0,916 |
45,361 |
46,277 |
|
12,500 |
0,170 |
-1,396 |
45,840 |
47,236 |
|
12,500 |
0,150 |
-2,401 |
46,845 |
49,246 |
|
12,500 |
0,140 |
-2,927 |
47,372 |
50,299 |
|
12,500 |
0,130 |
-3,471 |
47,916 |
51,387 |
|
12,500 |
0,120 |
-4,033 |
48,477 |
52,510 |
|
12,500 |
0,100 |
-5,213 |
49,657 |
54,870 |
|
12,500 |
0,000 |
-12,500 |
56,944 |
69,444 |
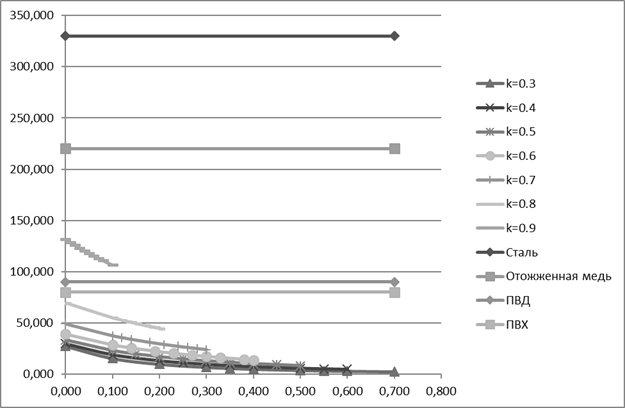
Рис. 2. Распределение максимальных напряжений по толщине
проводились для каждой десятой доли толщины трубопровода. Общее количество расчетных значений связано с толщиной трубопровода, которая фактически (см. рассуждения, приведенные ранее) определяется значением коэффициента формы в зависимости от внешнего радиуса. Чем больше задаем значение коэффициента формы, тем меньше расчетных значений по оси абсцисс можно получить. Именно этим обстоятельством объясняется «протяженность» полученных зависимостей. Например, для 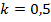 расчетными являются следующие доли толщины трубопровода:
расчетными являются следующие доли толщины трубопровода: 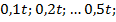 а при
а при 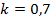 расчетными являются:
расчетными являются: 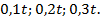
Представленные графики можно трактовать по-разному в зависимости от практических целей. Во-первых, с точки зрения расчета на прочность представленные зависимости показывают, что при заданном внутреннем давлении можно использовать любой из рассматриваемых материалов трубы, если выполняется ограничение для коэффициента формы 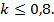 В этом случае максимальная толщина трубопровода не должна превышать значения, равного 20% от внешнего радиуса. При
В этом случае максимальная толщина трубопровода не должна превышать значения, равного 20% от внешнего радиуса. При 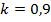 (толщина трубопровода составляет 10% от внешнего радиуса) следует использовать трубопроводы, выполненные только из отожженной меди или из стали. В этом случае уменьшается толщина трубопровода, следовательно, необходимо использовать более прочный материал. Выводы, сделанные на основе представленных расчетных зависимостей, полностью согласуются с требованием экономичности: чем прочнее материал, тем меньше толщина трубопровода и, соответственно, меньше материала требуется.
(толщина трубопровода составляет 10% от внешнего радиуса) следует использовать трубопроводы, выполненные только из отожженной меди или из стали. В этом случае уменьшается толщина трубопровода, следовательно, необходимо использовать более прочный материал. Выводы, сделанные на основе представленных расчетных зависимостей, полностью согласуются с требованием экономичности: чем прочнее материал, тем меньше толщина трубопровода и, соответственно, меньше материала требуется.
Во-вторых, обсуждаемые зависимости можно рассматривать и с другой точки зрения, с точки зрения подбора материала трубопровода. При конкретном (задаваемом) значении коэффициента 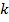 (и соответственно, известной толщине трубопровода) на основе имеющейся графической зависимости можно подобрать материал трубопровода по соответствующему конкретному значению расчетного сопротивления, допускаемого полученной графической зависимостью. Поэтому можно рассматривать представленные графические зависимости как один из вариантов проектирования материала трубопровода с заданными свойствами. Подобное решение позволит в определенных практических случаях рассматривать менее прочные (по величине расчетного сопротивления материала), но более выгодные с других точек зрения, материалы: например, новые материалы, более дешевые и т.п. Ведь каждый материал имеет свои достоинства и недостатки. Например, сталь имеет существенный запас прочности, но в то же время существует и проблема коррозии для трубопроводов, проводимых под землей, в агрессивной среде.
(и соответственно, известной толщине трубопровода) на основе имеющейся графической зависимости можно подобрать материал трубопровода по соответствующему конкретному значению расчетного сопротивления, допускаемого полученной графической зависимостью. Поэтому можно рассматривать представленные графические зависимости как один из вариантов проектирования материала трубопровода с заданными свойствами. Подобное решение позволит в определенных практических случаях рассматривать менее прочные (по величине расчетного сопротивления материала), но более выгодные с других точек зрения, материалы: например, новые материалы, более дешевые и т.п. Ведь каждый материал имеет свои достоинства и недостатки. Например, сталь имеет существенный запас прочности, но в то же время существует и проблема коррозии для трубопроводов, проводимых под землей, в агрессивной среде.
Далее на рис. 3 и рис. 4 представлены некоторые варианты расчета нормальных радиальных и окружных напряжений при конкретном значении коэффициента 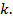 В этом случае на оси ординат показаны значения радиальных и окружных нормальных напряжений, а на оси абсцисс – значения долей толщины трубопровода. Как и раньше, расчеты выполнены для каждой десятой доли толщины трубопровода в пределах соответствующих ограничений, наложенных изменением коэффициента
В этом случае на оси ординат показаны значения радиальных и окружных нормальных напряжений, а на оси абсцисс – значения долей толщины трубопровода. Как и раньше, расчеты выполнены для каждой десятой доли толщины трубопровода в пределах соответствующих ограничений, наложенных изменением коэффициента 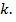 Графики показывают, что напряжения по толщине трубы изменяются по гиперболическому закону. На графиках очевидно постоянство начального и конечного значений радиальных напряжений. Это обосновывается тем, что значения сжимающих напряжений напрямую зависят от величины внутреннего давления, которое в данном расчете принято неизменным:
Графики показывают, что напряжения по толщине трубы изменяются по гиперболическому закону. На графиках очевидно постоянство начального и конечного значений радиальных напряжений. Это обосновывается тем, что значения сжимающих напряжений напрямую зависят от величины внутреннего давления, которое в данном расчете принято неизменным: 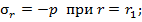
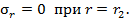 Максимальное значение окружных напряжений определяется значением коэффициента формы.
Максимальное значение окружных напряжений определяется значением коэффициента формы.
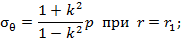
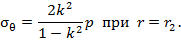
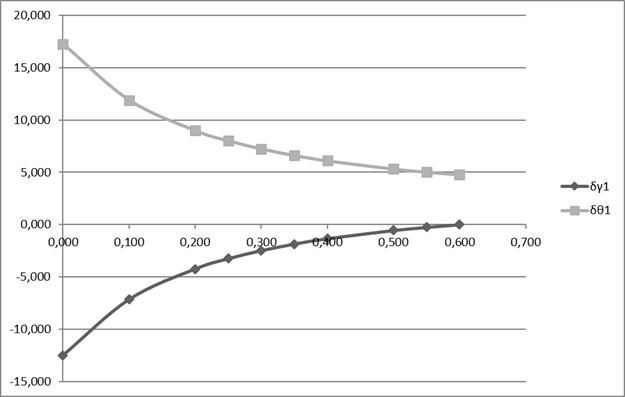
Рис. 3. Распределение нормальных и окружных напряжений по толщине при k=0.4
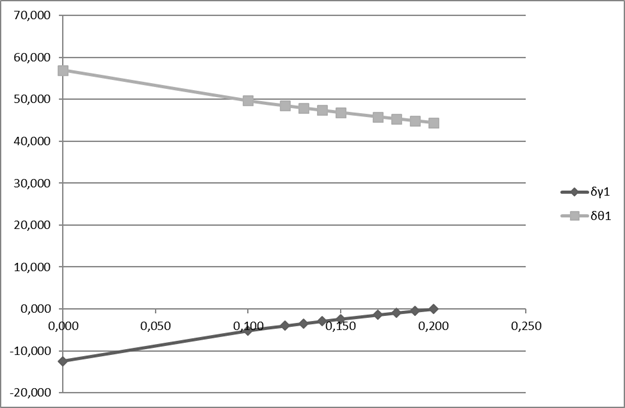
Рис. 4. Распределение нормальных и окружных напряжений по толщине при k=0.8
Таким образом, представленный частный вариант исследования радиальных и окружных нормальных напряжений в трубопроводе показывает возможность графического анализа нормальных напряжений в трубопроводе в зависимости от его материала и толщины.
Литература:
- СНиП 2.05.06-85 Магистральные трубопроводы.
- Сопротивление материалов / Под. ред. акад. АН УССР Писаренко Г. С.-5-е изд., перераб. и доп.-К.: Вища шк. Головное изд-во, 1986.-775 с.
- СНиП 3.05.05-84 Технологическое оборудование и технологические трубопроводы.







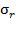 , МПа
, МПа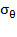 , МПа
, МПа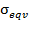 , МПа
, МПа