Рассматривается задача численного решения уравнения колебаний балки при разных типах граничных условий. Для этого был разработан новый численный подход к решению этой задачи, который, несмотря на недостаток в производительности по сравнению с численным методом, основанным на методе редукции, имеет ряд неоспоримых преимуществ.
Ключевые слова: колебания балки, жёсткое, шарнирное и свободное закрепление концов балки.
Введение. Колебания балки описываются гиперболическим по Петровскому уравнением
, 
,
,
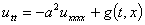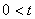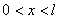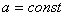, (1)
где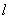 
– длина балки, 
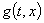– функция из некоторого класса, являющаяся внешним воздействием на процесс колебания балки и может представлять собой управляющую функцию. Начальные возмущения для задачи считаются известными
, 
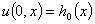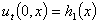. (2)
На концах балки можно наложить разные типы закреплений. В данной работе будут рассматриваться четыре них, а именно, шарнирный (нежёсткий) тип закрепления на обоих концах
, 
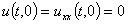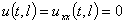, (3)
жёсткое закрепление на обоих концах
, 
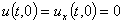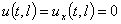, (4)
жёсткое закрепление одной стороны и свободный конец с другой стороны
, 
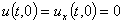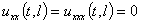, (5)
нежёсткое закрепление одной стороны и свободный конец с другой стороны
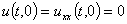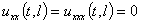, . (6)
Численный метод решения. Уравнение (1) представим в виде следующей системы
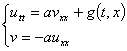(7)
Помимо представления (7) часто бывает удобно воспользоваться также следующим разложением
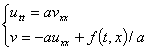, (8)
где
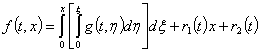(9)
Для определения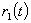 
, 
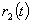воспользуемся тем фактом, что при симметричной функции 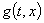, решение уравнения тоже должно быть симметричным. Тогда пусть 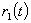и 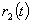такие функции, что 
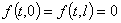. В результате из (9) получаем, что значения этих функций определяются следующим образом
, 
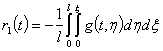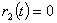(10)
Поэтому окончательное выражение для функции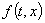 
будет иметь вид
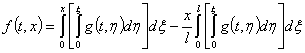(11)
В дальнейшем будет рассматриваться система (7), поскольку все выкладки для неё легко перенести и для системы (8).
Далее в рассматриваемой области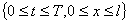 
введём сетку, для чего зададим натуральные числа 
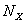и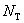 
, и разобьём её на прямоугольные ячейки параллельными прямыми 
, 
, 
, 
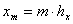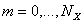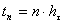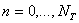, где 
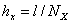и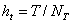 
являются шагами разностной сетки. Аппроксимируем системы (7) на этой сетке со вторым порядком аппроксимации [3], в результате получим следующую конечно-разностную схему
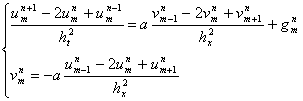(12)
Из (12) возникает вопрос, как мы сможем определить значение на 1-ом слое (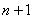
слой при 
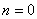), если нам необходимо значение функции 
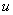на -1 слое. Для этого воспользуемся вторым условием в (2) и аппроксимируем его следующим образом
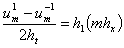(13)
Из (13) следует выражение функции 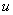на -1 слое
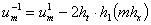(14)
Таким образом, из первого уравнения системы (12) и выражения (14) для слоя 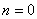получается, что
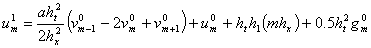(15)
Далее просто пользуемся схемой (12).
При переходе к системе (7) возникает необходимость определить граничные условия для появившейся функции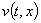 
. Рассмотрим условия (3) – (6) по отдельности.
Для граничных условий (3) получаются следующие соотношения
, 
, 
, 
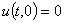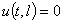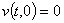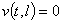, (16)
где для функции 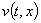условия получаются из второго уравнения в системе (7) и условий на вторые производные в (3).
Для граничных условий (4) получаются следующие соотношения
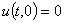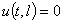, , (17)
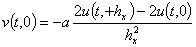, (18)
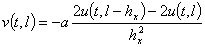, (19)
где для функции 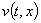из второго уравнения в системе (7) и условий на первые производные в (4), из которых получаются следующие равенства для сеточной функции 
, 
.
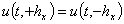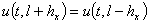Для граничных условий (5) для функци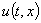й 
и 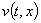условия определялись выше
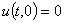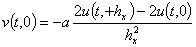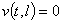, , , (20)
кроме значения функции 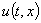в точке 
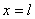. Для этого воспользуемся последними условиями в (5) и распишем их в виде конечно-разностных представлений
,
,
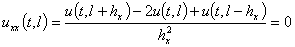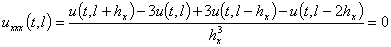из которых получается, что
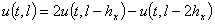(21)
Для граничных условий (6) все значения на границе мы уже определили выше:
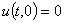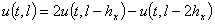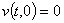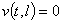, , , (22)
В случае использования системы (8) все граничные условия легко преобразовать с учётом функции .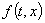
Начальное условие для функции 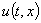будет определяться из первого равенства в (2), а для функции 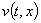– из второго уравнения системы (12).
Проверка на устойчивость методом Неймана [3] показала, что схема (12) условно устойчива. Подставив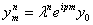 
в однородную систему (12), где 
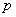– параметр, а 
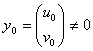, получается, что условная устойчивость достигается при соотношении [4]
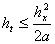(23)
Приведём примеры численного подхода к решению задачи (1)-(6). Для этого будем рассматривать свободные колебания балки при разных граничных условиях. При численном решении будут заданы следующие входные параметры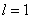 
, 
, 
, 
, 
.
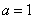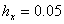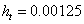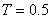Пример 1. Рассмотрим однородное уравнение (1), и пусть начальные возмущения задаются как следующие функции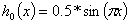 
, 
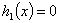. Тогда процесс свободного колебания 
будет иметь вид, указанный на рисунках с 1 по 4, соответственно, для четырёх граничных условия (3) – (6)
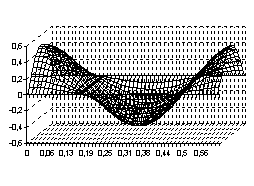
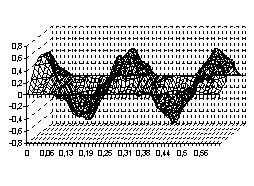
Рис. 1 Рис. 2
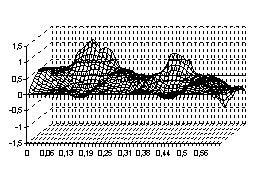
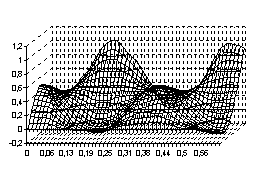
Рис. 3 Рис. 4
Пример 2. Рассмотрим однородное уравнение (1), и пусть начальные возмущения задаются как следующие функции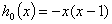 
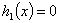, . Тогда процесс свободного колебания 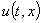будет иметь вид, указанный на рисунках с 5 по 8, соответственно, для четырёх граничных условия (3) – (6)
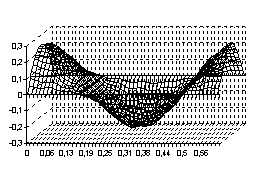
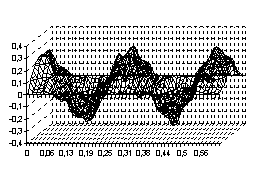
Рис. 5 Рис. 6
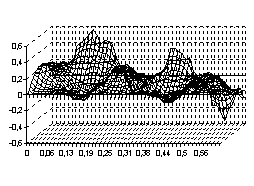
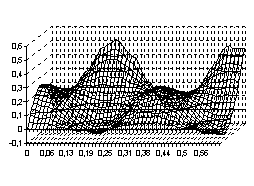
Рис. 7 Рис. 8
Пример 3. Рассмотрим однородное уравнение (1), и пусть начальные возмущения задаются как следующие функции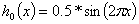 
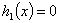, . Тогда процесс свободного колебания 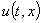будет иметь вид, указанный на рисунках с 9 по 12, соответственно, для четырёх граничных условия (9) – (12)
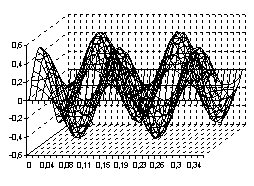
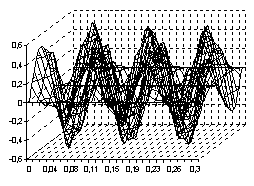
Рис. 9 Рис. 10
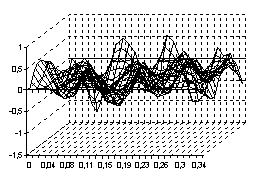
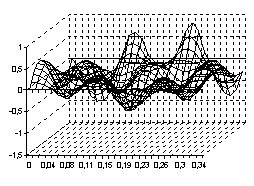
Рис. 11 Рис. 12
Для проверки, что численный метод решения задачи колебаний балки предложенный в данной статье, стремится к точному решению при уменьшении шагов сетки, воспользуемся правилом Рунге исследования сходимости и порядка разностных схем. Суть этого метода следующая, если выполняется следующее соотношение
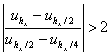, (24)
где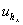 
, 
, 
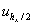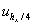– численные решения задачи (1) – (6) с шагами 
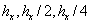, соответственно, то можно утверждать, что численный метод сходится к точному решению.
Для проверки будем использовать начальные условия 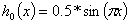, 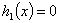и в качестве точки отсчёта возьмём шаг 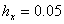. Тогда для граничных условий (3) при некоторых значени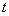й 
и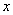 
получатся значения выражения (24), указанные в таблице 1.
Таблица 1
|
t = 0,1 |
t = 0,2 |
t = 0,3 |
t = 0,4 |
t = 0,5 |
t = 0,6 |
|
|
x = 0,1 |
3,98 |
3,99 |
4,03 |
3,98 |
3,98 |
4,06 |
|
x = 0,25 |
3,99 |
3,98 |
4,04 |
3,97 |
3,99 |
4,04 |
|
x = 0,75 |
3,99 |
3,98 |
4,04 |
3,97 |
3,99 |
4,04 |
|
x = 0,9 |
3,98 |
3,99 |
4,03 |
3,98 |
3,98 |
4,06 |
Нетрудно заметить, что условие (24) достигается.
Ранее уже предлагался численный подход к решению уравнения (1) на основе метода редукции [1, 2]. Предложенный в [1, 2] метод обладает неоспоримым преимуществом, поскольку конечно разностная схема, лежащая в его основе, является безусловно-устойчивой, что делает его быстрым и менее требовательным к ресурсам вычислительной машины. Однако его можно назвать хорошим образцом тех методов, которые используются в промышленных целях, поскольку высокая скорость достигается за счёт трудоёмкой алгоритмизации. В исследовательских целях экспериментаторам может понадобиться более прозрачный алгоритм, который будет позволять более просто вносить различные модификации в саму модель колебания балки. Метод, предложенный в данной статье, является хорошим примером простоты и лаконичности, что позволяет проводить эксперименты более очевидным образом, хотя и за счёт больших требований к ресурсам вычислительной машины.
Заключение. Таким образом, данный метод позволяет при различных типах граничных и начальных условий уравнения (1), получать решение уравнения.
Литература:
1. Атамуратов А.Ж.., Михайлов И.Е., Муравей Л.А. О гашении колебаний балки. // Труды ИСА РАН. Динамика неоднородных систем. Том 50(1). М.: Изд-во ЛКИ, 2010. С. 53-58.
2. Атамуратов А.Ж.., Михайлов И.Е., Муравей Л.А. О гашении колебаний сложных механических структур. //Научно-технический журнал. Авиакосмическая техника и технология. Выпуск 4. М.: ИТЭП, 2012. С. 54 – 59.
3. Самарский А.А., Гулин А.В. Численные методы. М.: Наука. 1989. 432 с.
4. Атамуратов А.Ж. Исследование устойчивости двух конечно разностных схем для численного решения уравнения колебаний балки. // Молодой ученый. №1. 2014. С. 1-7. http://www.moluch.ru/archive/60/8637/
