Рассматривается задача разработки и использования методов параллельного программирования при численном решении задач оптимизации методами координатного и градиентного спусков. Задача оптимизации рассматривается в контексте решения задачи гашения колебаний таких элементов механических структур как прямоугольные мембраны, балки и прямоугольные пластины.
Ключевые слова: параллельное программирование, метод координатного спуска, метод градиентного спуска, прямоугольная мембрана, балка, прямоугольная пластина, уравнение колебаний, численное решение, библиотека OpenMP.
Введение. Большинство задач оптимизации и математической физики являются очень сложными для решения их аналитическим способом, например, задачи гашения колебаний элементов механических структур, таких как прямоугольные мембраны, балки и прямоугольные пластины [1–14]. Поэтому огромное практическое значение имеет умение решать такие задачи численным способом, то есть аппроксимация исходной задачи конечно разностными схемами и использование существующих классических подходов к оптимизации заданного функционала методами координатного и градиентного спусков. Подобные методики дают приближённое решение, которое при увеличении точности стремится к аналитическому решению. Но с увеличением точности, а под час и при простейшей реализации численного алгоритма требование к производительности вычислительной машины может возрастать чуть ли не экспоненциально. Для того чтобы, если и не избежать таких моментов, но, по крайней мере, обойти их, необходимо использовать нестандартные подходы к проектированию комплекса программ, основанные на использовании алгоритмов параллельного программирования.
В этой работе будет показано, как можно эффективно выстроить численный алгоритм в программном комплексе на основе параллельного программирования так, чтобы скорость выполнения программ значительно увеличилась.
Особенности разработки параллельных алгоритмов. Если несколько задач выполняются в течение одного и того же временного интервала, то говорят, что они выполняются параллельно. Другими словами, задачи, которые существуют в одно и тоже время и выполняются в течение одного и того же интервала времени, являются параллельными. Основной фактор, влияющий на степень приемлемости для параллелизма того или иного интервала времени, определяется конкретным приложением. Цель технологий параллелизма — обеспечить условия, позволяющие компьютерным программам делать больший объём работы за тот же интервал времени. Поэтому проектирование программ должно ориентироваться не на выполнение одной задачи в некоторый промежуток времени, а на одновременное выполнение нескольких задач, на которые предварительно должна быть разбита программа.
Методы параллельного программирования позволяют распределить работу программы между двумя (или больше) процессорами в рамках одного физического или одного виртуального компьютера. При этом процесс проектирования таких программ включает в себя три составляющие: декомпозиция, связь и синхронизация. При этом в современных библиотеках для параллельного программирования за обеспечение связи и синхронизации отвечает сама библиотека и набор функций, например, в библиотеке OpenMP. Поэтому главное, на что необходимо обратить внимание, — это декомпозиция. Декомпозиция — это процесс разбиения задачи и её решения на части. Декомпозиция программного обеспечения часто сводится к декомпозиции работ. Одна из основных проблем параллельного программирования — идентификация естественной декомпозиции работ для программного решения. Главная цель — обнаружить параллелизм. Если естественный параллелизм не наблюдается, не стоит его навязывать насильно. На вопрос, как разбить приложение на параллельно выполняемые части, необходимо найти ответ в период проектирования. Параллелизм можно обеспечить на уровне инструкций, подпрограмм, объектов или приложений.
Постановка задачи гашения. В целях рассмотрения задачи введения параллельности в задачу оптимизации необходимо начать с постановки задач, которые приводят к необходимости использования параллельных алгоритмов. Будут рассматриваться три задачи, имеющие огромную практическую ценность для науки и общества в целом: гашение колебаний балки, гашение колебаний прямоугольной мембраны и пластины [1–14].
Колебания балки описываются гиперболическим по Петровскому уравнением
, 
,
,
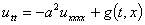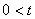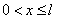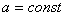, (1)
со следующими начальными и граничными условиями
, 
, 
, 
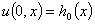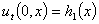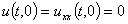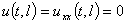. (2)
Колебания прямоугольной мембраны описываются уравнением общего вида
, 
,
,
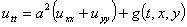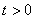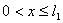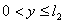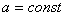,. (3)
со следующими начальными и граничными условиями
, 
, 
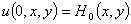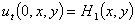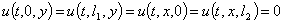. (4)
Малые поперечные колебания упругой изотропной пластины постоянной толщины описываются уравнением Жармен-Лагранжа
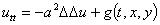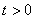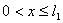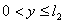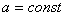, ,,,. (5)
со следующими начальными и граничными условиями
, 
, 
, 
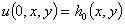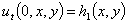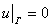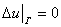(6)
Задача гашения ставится для всех трёх структур так [1–14]: требуется найти управляющую функцию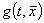 
из пространства 
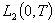, где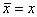 
для балки и 
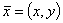для мембраны и пластины, позволяющую за минимальное время 
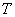, полностью погасить колебания, что определяется условием 
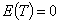равенства нулю интеграла энергии соответствующей механической структуры. Познакомиться с видом интегралов энергии и их выводом можно ознакомиться здесь [6].
В зависимости от задачи функция 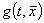могла принимать разные формы, но в общем виде она разбивалась на две составляющие: функцию импульса
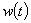и функцию расположения на структуре 
.
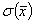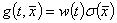(7)
При аппроксимации [15–17] функции 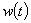кусочно-постоянной функцией 
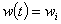, где 
, 
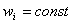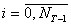для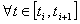 
интеграл энергии получается функцией переменных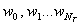 
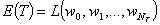(8)
Таким образом, задача гашения колебаний сводится к поиску такой комбинации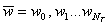 
, при которой выполняется условие 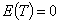, что можно делать с помощью как метода градиентного спуска, так и метода координатного спуска [15–17].
Методы градиентного и координатного спусков и необходимость параллелизации. Метод градиентного спуска заключается в следующем [15–17]. Выбрав произвольное начальное приближение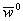 
, строится следующая итерационная последовательность
, 
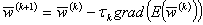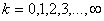(9)
где величины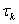 
выбирается достаточно малыми из условия 
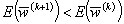. Сам же итерационный процесс (9) завершается в случае, если было достигнуто условие на значение интеграла энергии 
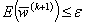или если перестали меняться значения функции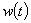, то есть 
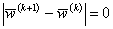. Вспоминая, что 
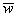— это вектор, тогда в скалярной форме (9) примет вид
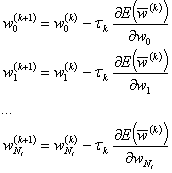(10)
Метод координатного спуска заключается в следующем [15–17]. Выбрав произвольное начальное приближение 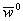, зафиксируем координаты 
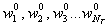и найдём значение 
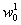как решение задачи
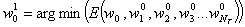(11)
каким-либо методом поиска минимума функции одной переменной, например, методом парабол. Далее аналогично находим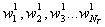 
как решения задач одномерной оптимизации
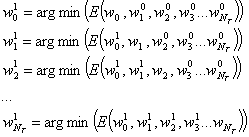(12)
На этом первая итерация заканчивается, и весь итерационный процесс состоит из последовательных решений задач минимизации по отдельным координатам.
Отдельно стоит упомянуть о методе парабол для задачи одномерной оптимизации, о котором упоминалось выше и детали которого понадобятся дальше. Для начала выбираем шаг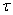 
, с которым будем производить смещения. Затем, для определения на первой итерации
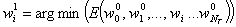(13)
необходимо сделать три шага и получить три значения интеграла энергии в трёх точках, а именно
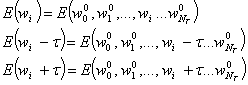(14)
По этим трём значениям можно построить параболу
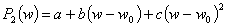, (15)
где коэффициенты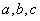 
находят из
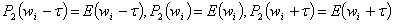(16)
От сюда получаем, что
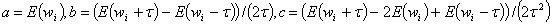(17)
Далее ищем минимум параболы (15) и исходя из этого определяется значение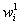 
и так далее.
Оба метода, и градиентный и координатный спуск, являются классическими методами оптимизации, которые приводят к результату. Но в зависимости от сложности задачи и нетривиальности функционала минимизации, они могут быть очень неэффективными в плане скорости сходимости. Ранее уже разрабатывались подходы к улучшению этих методов, в частности для метода градиентного спуска были разработана методы увеличивающие скорость сходимости посредством модификации самого метода [15–17]. Но всё это решает проблему отчасти. Попробуем воспользоваться современными компьютерными технологиями, что исправить данную ситуацию и воспользуемся методами параллельного программирования для ускорения работы классических методов оптимизации.
Параллелизация классических методов оптимизации. Рассматривая классические методы оптимизации, такие как методы градиентного и координатного спусков, необходимо определить есть ли место для естественной параллелизации и, если есть, то где именно её можно встроить.
Если вспомнить про скалярную форму метода градиентного спуска (10), можно заметить что она содержит в себе возможность для естественной параллелизации на уровне инструкций, поскольку каждый сдвиг по каждой координате на зависит от других координат. В обычной последовательной реализации метод градиентного спуска выглядит для одной итерации как на рис. 1
Рис. 1. Метод градиентного спуска в последовательном исполнении.
В случае же использования параллельного программирования программный код можно преобразовать так, чтобы каждый шаг по каждому параметру в (10) выполнялся параллельно остальным, а именно
Рис. 2. Метод градиентного спуска в параллельном исполнении.
Для этого можно использовать следующую языковую конструкцию (здесь и далее будет использоваться псевдоязык программирования как совмещение языка программирования C, библиотеки OpenMP и математических формул)
#pragma omp parallel for schedule(dynamic, 1)
for(int k=0; k<=NT-1; k++)
{
;
}
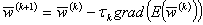Данная директива (#pragma omp parallel) заставит для каждого k проводить вычисления параллельно на всех доступных процессорах (ядрах) вычислительной машины. При этом библиотека берёт на себя заботу о связи и синхронизации.
В случае же метода координатного спуска при рассмотрении записи (12) можно увидеть, что в ней нет возможности для естественной параллелизации, поскольку для определения очередного значения координаты используется только что найденное значение предыдущей координаты. Но возможность для естественной параллелизации существует в тот момент, когда мы используем метод одномерной оптимизации по конкретной координате, а именно, метод парабол (14), поскольку шаги по координате делаются независимо друг от друга. Поэтому в последовательном исполнении это выглядит как на рис. 3.
Рис. 3. Метод парабол в методе координатного спуска в последовательном исполнении.
В случае же использования параллельного программирования программный код можно преобразовать так, чтобы каждый из трёх шагов в (14) выполнялся параллельно остальным, а именно
Рис. 4. Метод парабол в методе координатного спуска в параллельном исполнении.
Для этого можно использовать следующую языковую конструкцию
#pragma omp parallel sections
{
#pragma omp section
{
}
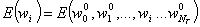
#pragma omp section
{
}
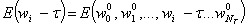
#pragma omp section
{
}
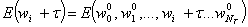
Заключение. Врезультате этих манипуляций с программным кодом можно значительно сократить время выполнения программы, сократить время сходимости. Однако стоит учитывать ряд особенностей. Для параллелизации метода градиентного спуска время сходимости уменьшается пропорционально количеству процессоров, однако количество координат, по которым осуществляется спуск, может значительно превосходить количество доступных процессоров, поэтому возможности параллелизации не будут использованы полностью. Однако это можно решить за счёт выделения дополнительных вычислительных мощностей. В случае же метода парабол в методе координатного спуска могут использоваться всего лишь 3 процессора, поскольку в методе делается 3 шага, и даже при наличии сводных мощностей, они будут просто простаивать.
Литература:
1. Атамуратов А. Ж., Михайлов И. Е., Муравей Л. А.. О гашении колебаний балки. // Труды ИСА РАН. Динамика неоднородных систем. Том 50(1). — М.: Книжный дом «ЛИБРОКОМ», 2010. — С. 53–58.
2. Атамуратов А. Ж., Михайлов И. Е., Муравей Л. А. О гашении колебаний сложных механических структур // Авиакосмическая техника и технология, 2012, № 4. С. 54–59.
3. Атамуратов А. Ж. О гашении колебаний прямоугольной мембраны // Вестник Тверского государственного университета. Серия Прикладная математика. — 2013. — № 2. — С. 49–59.
4. Атамуратов А. Ж. Исследование подходов к решению задач математической физики на примере уравнения колебаний прямоугольной мембраны // Молодой ученый. № 10. 2013. С. 1–5. http://www.moluch.ru/archive/57/6198/
5. Атамуратов А. Ж. Приведение к тригонометрической проблеме моментов на примере задачи гашения колебаний прямоугольной мембраны, балки и прямоугольной пластины // Молодой ученый. № 11. 2013. С. 6–10. http://www.moluch.ru/archive/58/8092/
6. Атамуратов А. Ж. Получение интегралов энергии для прямоугольной мембраны, балки и прямоугольной пластины // Молодой ученый. № 11. 2013. С. 10–15. http://www.moluch.ru/archive/58/8112/
7. Атамуратов А. Ж., Михайлов И. Е. Численное решение задачи о гашении колебаний балки. Тезисы докладов Международной конференции по прикладной математике и информатике, посвященной 100-летию со дня рождения академика А. А. Дородницына. ВЦ РАН, Москва, 7–11 декабря 2010 г. С. 83–84.
8. Muravey L., Mikhailov I., Atamuratov A., The damping problem of vibrations for large mechanical systems // ICIAM2011, Abstracts, Vancouver, Canada, July 18–22, 2011. P. 87.
9. Atamuratov A., Mikhailov I., Muravey L. On the numerical damping of beam’s vibrations // VII International Aerospace Congress IAC’12. Abstracts. Moscow, Russia. 26–31 August, 2012. P. 31–32.
10. Атамуратов А. Ж. Решение уравнения колебаний балки. // XXXV ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференции. Москва, апрель 2008 г. Москва: МАТИ, 2008. Т.5.
11. Атамуратов А. Ж. О гашении колебаний балки. // XXXVI ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференции. Москва, апрель 2010 г. Москва: МАТИ, 2010. Т.5.
12. Атамуратов А. Ж. О гашении колебаний прямоугольной мембраны. // XXXVII ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференции в 8 томах. Москва, 5–8 апреля 2011 г. Москва: МАТИ, 2011. Т.5, С. 60–61
13. Атамуратов А. Ж. Решение уравнения колебаний круглой пластины. // XXXVIII ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференции в 8 томах. Москва, 10–14 апреля 2012 г. Москва: МАТИ, 2012. Т.5, С. 38–39
14. Атамуратов А. Ж. Численный метод решения колебаний прямоугольной пластины. // XXXIX ГАГАРИНСКИЕ ЧТЕНИЯ. Научные труды Международной молодёжной научной конференции в 9 томах. Москва, 9–13 апреля 2013 г. Москва: МАТИ, 2013. Т.5, С. 32–33
15. Самарский А. А., Гулин А. В. Численные методы. Москва: Наука, 1989. 432 с.
16. Формалёв В. Ф., Ревизников Д. Л. Численные методы. Москва: ФИЗМАТЛИТ, 2006. 400 с.
17. Ращиков В. И., Рошаль А. С. Численные методы решения физических задач. СПб: Издательство «Лань», 2005. 208 с.
18. Шилдт Г. Полный справочник по C. Москва: Издательский дом «Вильямс», 2004. 704 с.
