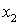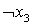Проблема выполнимости булевых формул (проблема пропозициональной выполнимости) — это одна из наиболее известных NP-полных задач. Несмотря на то, что в общем случае проблема выполнимости не разрешима за полиномиальное время, нахождение случаев, когда ответ может быть получен быстро, очень важно для различных прикладных задач. В частности, тесты, основанные на проблеме выполнимости сегодня широко применяются для автоматизации проектирования, а также для проверки разрабатываемых программ. С другой стороны, выявление сложных случаев задачи о выполнимости, позволяет реализовывать более эффективные системы защиты информации.
Тема сведения задач из различных областей прикладной математики и информатики к задаче выполнимости хорошо развивается. Одна из причин этого — возможность решать задачи, возникающие в самых различных областях, единым алгоритмом решения задачи выполнимость [1].
Задача выполнимости может быть решена с помощью сведения к задаче о минимальном покрытии. Эффективность решения задачи методом групповых резолюций зависит от исходных данных, поэтому важной задачей является определение области применения, в которой рассмотренный алгоритм работает наиболее эффективно, другими словами поиск подмножества задач, для которых алгоритм находит оптимальное решение за допустимое время.
Базовый метод групповых резолюций
Метод групповых резолюций позволяет найти решения задачи о минимальном покрытии (0,1) — матрицы B множеством строк. Пусть дана система дизъюнктов.
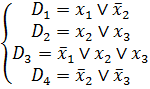
Для нее строим (0,1) — матрицу В следующим образом. Строки матрицы соответствуют литералам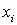 
и их отрицаниям 
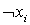. Таким образом, число строк составит 2n, где n — число различных булевских переменных. Столбцы матрицы соответствуют дизъюнктам системы Dj, причем столбец содержит единицу в строке 
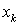и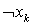 
, если переменная 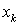входит в Dj без отрицания (с отрицанием). Кроме того, матрица дополнительно содержит n столбцов, соответствующих тавтологическим дизъюнктам 
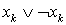. С учетом сказанного, матрица В для рассматриваемого примера имеет вид, изображенный в таблице 1.
Таблица 1
Исходная матрица
|
D1 |
D2 |
D3 |
D4 |
D5 |
D6 |
D7 |
|
|
|
1 |
1 |
|||||
|
|
1 |
1 |
1 |
||||
|
|
1 |
1 |
1 |
||||
|
|
1 |
1 |
|||||
|
|
1 |
1 |
1 |
||||
|
|
1 |
1 |
Под минимальным покрытием матрицы В понимается минимальное по числу строк множество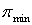 
, такое, что для каждого столбца матрицы В найдется как минимум одна строка в 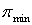, которая содержит в данном столбце «1» (иными словами, покрывает данный столбец).
Утверждение. Пусть дана матрица В, построенная для системы дизъюнктов с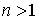 
переменными. Если минимальное покрытие 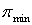матрицы В содержит более n строк, то данная система дизъюнктов невыполнима; в противном случае — выполнима [2].
Принцип групповых резолюций позволяет порождать новые — групповые резольвенты, используя любой эвристический метод для отыскания минимального или близкого к нему покрытия. Гарантируется, что рано или поздно будет порожден полностью нулевой столбец. В этом случае алгоритм прекращает работу. Наилучшее из найденных к этому моменту покрытий и является минимальным.
В качестве эвристического алгоритма используется описанный ниже. На каждой итерации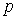 
отыскиваем столбец (из числа невычеркнутых) с минимальным числом единиц. Обозначим этот столбец 
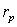и назовем его синдромным. Найдем невычеркнутую строку 
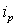, покрывающую 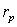, и такую, что из всех других строк, покрывающих 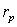, она содержит наибольшее число единиц. Включим 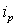в отыскиваемое на данной итерации 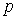покрытие. Вычеркнем все строки, содержащие в столбце 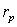«1», а также все столбцы, покрываемые строкой 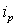. Итерация ведется до тех пор, пока имеется хотя бы один невычеркнутый столбец и одна невычеркнутая строка.
Так берем столбец D1 и строку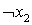 
, которую включим в отыскиваемое покрытие на итерации 1. Вычеркнем строки и столбцы согласно описанному правилу. Результат описан в таблице 2.
Таблица 2
Матрица на второй итерации
|
D2 |
D3 |
D5 |
D7 |
|
|
1 |
1 |
|
|
|
1 |
1 |
1 |
|
|
1 |
1 |
|
|
|
1 |
Выполним теперь вторую итерацию. Выберем столбец D2 и строку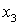 
. Вычеркнем строки и столбцы согласно описанному выше правилу (см. таблицу 3).
Таблица 3
Матрица на последней итерации
|
D5 |
|
|
|
1 |
|
|
Остается единственный не вычеркнутый столбец, так что включаем строку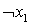 
в предполагаемое минимальное покрытие. Таким образом, итерация завершается отысканием покрытия 
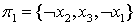. Согласно представленному выше утверждению, данное покрытие минимально и дает выполняющую интерпретацию для исходной системы дизъюнктов.
Описанный эвристический алгоритм не всегда отыскивает минимальное покрытие, и необходимо выполнять этап построения групповой резольвенты следующим образом. Берется текущее найденное покрытие и оставляется в нем любые n+1 строк. Формируется матрица R из синдромных столбцов, найденных для этих строк. Формируется столбец-резольвента, исходя из следующего: столбец содержит «1» в тех и только тех строках, которые в R имеют две или более единиц; в противном случае строка содержит «0». Этот столбец присоединяется к матрице В, и итерации возобновляются снова [2].
Найденное на первой итерации покрытие 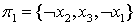содержит n=3 строки. Построим для него матрицу R на синдромных столбцах D1, D2, D5 (см. таблицу 4).
Таблица 4
Построение резольвенты
|
D1 |
D2 |
D5 |
Резольвента |
|
|
1 |
1 |
1 |
|
|
1 |
||
|
|
1 |
||
|
|
1 |
||
|
|
1 |
||
|
|
В данном случае групповая резольвента содержит единственную «1» в строке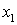 
. При возобновлении итераций (если бы это было необходимо) следует добавить данную резольвенту к матрице В.
Для матриц небольших размеров описанный алгоритм показывает хорошие результаты. Например, минимальное покрытие для матрицы 30х100 с плотностью 0,08 в среднем находится менее, чем за 1000 итераций (время выполнения 1–2 с).
Однако алгоритм обладает следующими недостатками для матриц больших размеров:
- Нелинейная зависимость количества итераций от размера матрицы.
- Рост размеров матрицы вследствие добавления новых резольвент на каждой итерации.
Разработка усовершенствованного метода
Базовая версия алгоритма способна найти оптимальное решение, но на небольших матрицах. Если количество строк превышает отметку в 30 штук или столбцов в 50, то время вычисления становится неуместным [2]. Основной проблемой такого подхода является быстрый рост количества добавляемых резольвент, что значительно снижает показатели расхода памяти. Также, с добавлением новой резольвенты растет и время работы алгоритма на следующей итерации.
В качестве места для оптимизации алгоритма было решено взять процесс построение групповой резольвенты. Тогда на этапе подготовки массива уже существующие групповые резольвенты не перетираются. Новая резольвента добавляется в конец массива, сбрасываются все статусы строк и столбцов и начинается этап поиска решения.
После нахождения некоторого решения необходимо построить групповую резольвенту. Процесс построения похож на базовую реализацию за исключением того, что единица в резольвенте ставится только одна и в той строке, которая содержит в себе наибольшее количество единиц в матрице, составленной из синдромных строк и столбцов. Такой подход ограничивает рост матрицы.
Поскольку вновь созданные групповые резольвенты не перетирают старые, то возникает возможность роста размера матрицы. Однако, из-за того, что в созданных резольвентах лишь одна единица, то это обеспечивает гарантированно попадание пересекаемой строки в решение. А тот факт, что новые резольвенты строятся на основе синдромных строк и столбцов, гарантирует, что одна и та же резольвента не будет сгенерирована дважды. Она гарантированно попадет в решение вместе с соответствующим столбцом-резольвентой, однако в ней будет лишь одна единица. Остальные столбцы будут вычеркнуты на этапе поиска решение и не смогу стать синдромными.
Итак, на каждой итерации гарантированно находится строка, попадающая в решение. Поскольку созданные резольвенты не перетираются между итерациями, а максимальное количество строк в решении равно начальному количеству строк, то и количество столбцов, как и в базовой версии, не превысит значение m+n. Более того, количество итераций ограничивается количеством строк, что не дает расти времени вычисления алгоритма. Ограничение количества операций позволяет больше не задумываться об этом аспекте алгоритме, а все дальнейшие оптимизации могут быть направлены лишь на увеличение производительности второго этапа.
Статистический анализ результатов работы метода
На рисунке 1 приведен график, показывающий рост количества итераций в зависимости от размера матрицы (количества строк). Значение плотности «1» было взято равное 0.2. Как видно из графика, количество итераций растет пропорционально функции √x и достаточно медленно (для матрицы размером 990 строк на 990 столбцов необходимо в среднем чуть менее 19 итераций).
Также, было замечено, что совсем необязательно ждать окончания всех итераций. Вторая линия на графике 1 показывает номер лучшей итерации в решении, т. е. той, на которой было найдено лучшее решение. Преждевременное прерывание алгоритма позволит значительно снизить затраты на вычисления. Как видно из графика, при нахождении достоверного условия о нахождении наилучшего решения количество итераций можно снизить примерно в 3 раза.
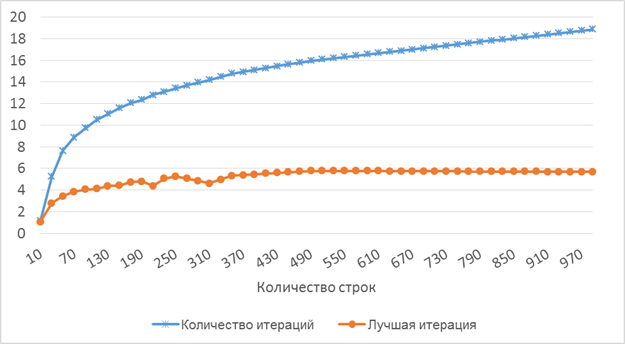
Рис. 1. График зависимости количества итераций и номера лучшей итерации от размера матрицы (плотность 0.2)
Для более наглядной демонстрации возможностей алгоритма при проведении расчетов замерялось, также, и количество времени, затраченное на решение. На рисунке 2 приведен график зависимости затраченного времени от размера матрицы при фиксированной плотности (0.2). Измерения проводились на ПК с конфигурацией: Intel Core i5–3450 3.10GHz, 8Gb RAM, Windows 7 x64. Временные затраты растут по графику ветки параболы и для матрицы достаточно большого размера (около 1000 строк) не превышают 1.5 секунд.
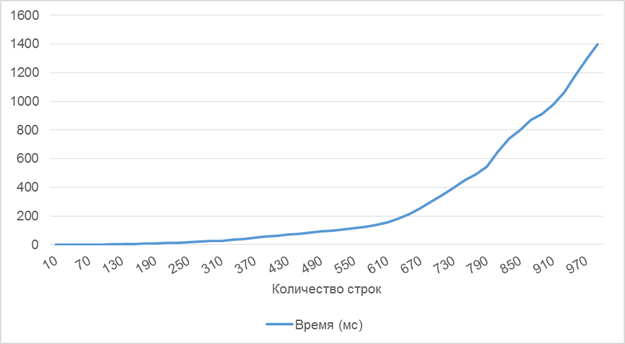
Рис. 2. График зависимости количества затраченного на решение времени в миллисекундах от размера матрицы
Для поиска зависимостей между производительностью алгоритма и плотностью единиц в матрице было решено использовать матрицы размером 200 строк на 200 столбцов и фиксировать количество итераций для разных значений плотностей «единиц» в матрицах. Как видно по графику на рисунке 5.3 количество итераций снижается по мере роста плотности.
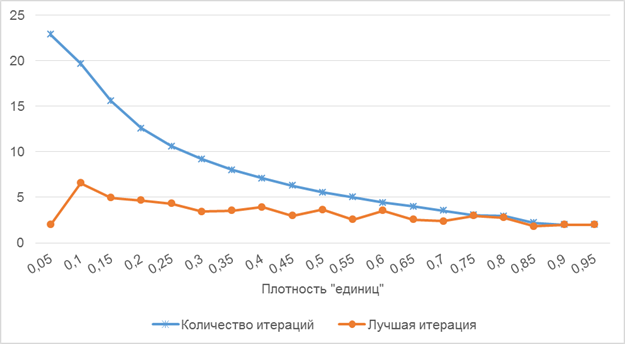
Рис. 3. График зависимости количества итераций и номера лучше итерации от плотности «единиц»
В процессе проведения вычислений, как и ожидалось, были выявлены слабые места алгоритма. В целом, алгоритм показал себя хорошо, особенно на матрицах с большой плотностью «единиц» вне зависимости от размера.
Для исследования поведения «желоба» неоптимальных решений был проведен ряд тестов не «вглубь», а «вширь», т. е. изучена зависимость нахождения оптимальных решений от размера матрицы. Для этого было зафиксировано количество строк (300 штук), а количество столбцов увеличивалось, начиная с 40 и далее. Таким образом, удалось установить зависимость нахождения оптимального решения от отношения количества строк к количеству столбцов (т. е. начиная с 40/300=0.13). Для общего представления приведен график на рисунке 4. Более крупный вид «желоба» (плотность «единиц» от 0.01 до 0.2) приведен на рисунке 5.
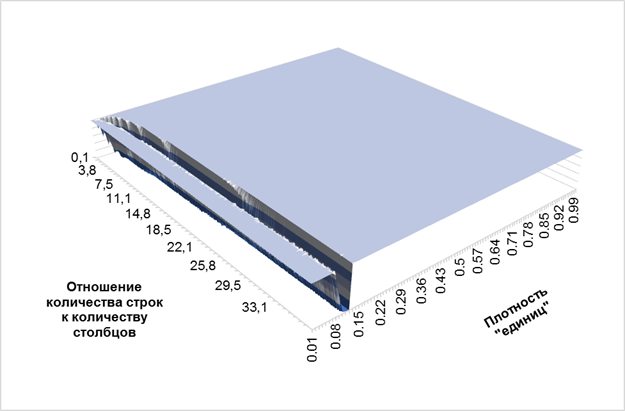
Рис. 4. Зависимость вероятности получения оптимального решения от размера матрицы и плотности «единиц»
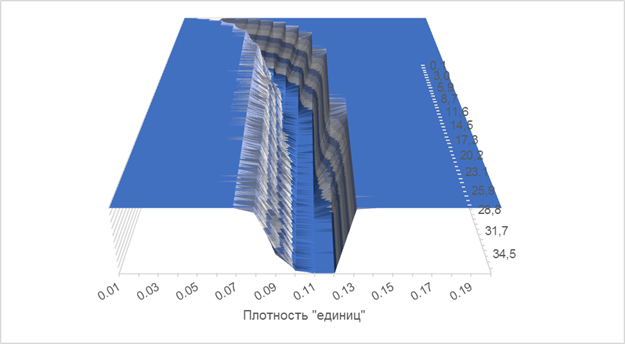
Рис. 5. Зависимость вероятности получения оптимального решения от размера матрицы и плотности «единиц». Детальный вид.
Заключение
Как видно из анализа полученных данных, получить абсолютно верно работающий алгоритм так и не удалось. Однако был сделан огромный шаг в сторону контроля количества итераций и, как следствие, времени расчета. Проанализировав полученные результаты был составлен список рекомендаций для направления вектора дальнейших исследований:
- Преждевременная остановка алгоритма — как видно из рисунков 1 и 3 лучшая итерация наступает намного раньше, чем условие окончания вычислений вне зависимости от размера матрицы. Особенно это заметно на матрицах с низкой плотностью «единиц»;
- Сокращение расходов на память — в худшем случае алгоритм требует хранить матрицу размером n×m+n (где n — количество строк в начальной матрице, m — количество столбцов). Под таким случаем мы подразумеваем матрицу, для которой решением будут все строки. Однако для матриц с большой плотностью необходимо значительно меньше итераций, чем количество строк. Отсюда можно сделать вывод, что совсем необязательно выделять изначально такие объемы памяти;
- Распараллеливание вычислений — в целом алгоритм достаточно линеен и каждая последующая итерация зависит от предыдущей (необходима вновь построенная дополнительная резольвента). Однако некоторые части вполне пригодны для распараллеливания: цикл для построения групповой резольвенты, циклы поиска минимального столбца, максимальной строки, вычеркивание синдромных строк и столбцов.
- Исследование проблемной зоны — как выяснилось, алгоритм ведет себя не самым лучшим образом на некоторых значениях плотностей «единиц». Пожалуй, это и есть его самый большой недостаток. Вероятность отыскания оптимального решения падает так низко, что использовать его на таких матрицах не целесообразно. И хотя ширина «желоба» ошибок не превышает 0.06 (это составляет всего 6 % от всего числа матриц), результаты на этом промежутке неудовлетворительны.
Новый метод основан на эмпирическом подходе, что не обеспечивает гарантированного 100 %-го результата. Однако были проведены тысячи опытов и анализ полученных результатов показал, что примерно в 94 % случаев метод выдает весьма находит оптимальное решение.
Улучшенная версия алгоритма хоть и не является точным подходом, но все же показывает почти 100 %-ые результаты. Такие данные подталкивают к дальнейшим исследованиям данного алгоритма, т. к. успех в решении одной задачи значительно расширит знания в области NP-полных задач в целом и задачи выполнимости в частности.
Литература:
1. Поцелуевская, Е. А. Теоретическая и практическая сложность задачи о выполнимости булевых формул / Интеллектуальные системы, 2009. С. 455–476.
2. Герман, О. В. Экспертные системы: учебно-методическое пособие / О. В. Герман — Минск БГУИР, 2008. С. 37–44.
