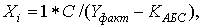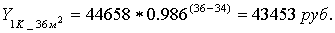Основные особенности и проблемы построения математической мультипликативной регрессионной модели для оценки стоимости жилой недвижимости

Как показывает практика, представленная ниже мультипликативная математическая регрессионная модель очень хорошо подходит для массовой оценки рыночной стоимости объектов жилой недвижимости в крупных городах России, в частности, для определения направления и степени влияния на удельную стоимость жилья основных его ценообразующих факторов [1]:

                          

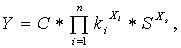
где: Y — цена 1 кв.м. анализируемого объекта; C — цена 1 кв.м. объекта с базовыми параметрами; Х_i — переменные, описывающие качественные характеристики объектов (ценообразующие факторы); k_i — коэффициенты, описывающие влияние на цену 1 кв.м. объекта его качественных признаков Х_i; n — количество данных факторов (Х_i); Х_S — переменная, описывающая количественную характеристику объекта — отклонение текущей площади от базовой; S — коэффициент, отражающий влияние на цену 1 кв.м. объекта его количественного признака Х_s.

Как и все другие, методика определения цены на основе представленной модели имеет свои определенные особенности и сложности, основные из которых изложены ниже.

1.    Проблема учета в модели аддитивно-влияющих факторов.

Предлагаемая модель является мультипликативной в общем виде, соответственно предполагается, что все включенные факторы влияют на анализируемый объект мультипликативно, что соответствует логике ценообразования на рынке. Однако могут возникать случаи, когда при построении модели необходимо учесть некоторые явно аддитивные факторы, при этом их мультипликативный учет может привести к некоторому искажению результатов модели.

Примером такого фактора может служить уровень ремонта в квартире. Если учитывать в модели данный фактор на ряду с другими как мультипликативный, то получится следующее: к примеру, если в квартире есть «хороший ремонт», который увеличивает стоимость 1 кв.м. в среднем 8–10 %, то абсолютная величина корректировки будет варьироваться в зависимости от типа дома, материала стен, района и т. п. Однако может возникнуть ситуация, когда в качестве «хорошего ремонта» необходимо рассматривать конкретную усредненную величину — например 4 тыс. руб. на 1 кв.м. независимо от цены «квадрата».

При этом можно предложить простой и понятный механизм, который позволит без изменения структуры модели заметно минимизировать возможные погрешности при мультипликативном учете аддитивного фактора [2]. Согласно концепции модели значение переменной X, описывающей, к примеру, фактор ремонта, будет равно 1 либо 0 в зависимости от того, сделан ли ремонт в конкретном анализируемом объекте или нет. Пусть стоимость 1 кв.м. базового объекта составляет 40 тыс. руб. В случае, если значение соответствующего коэффициента k составит 1,1, то получим, что для более дорогого объекта со стоимостью 1 кв.м. в 45 тыс. руб. (без ремонта) ремонт будет «накидывать» в среднем 4,5 тыс. руб., а для более дешевого в 35 тыс. руб. (без ремонта) — 3,5 тыс. руб. соответственно. Итоговая расчетная стоимость 1 кв.м. рассмотренных объектов составит 49,5 и 38,5 тыс. руб. соответственно, хотя фактическая составила бы 49 и 39 тыс. руб.

Таким образом, для того, чтобы в обоих объектах ремонт увеличивал удельную стоимость в среднем на 4 тыс. руб., необходимо просто подкорректировать (пересчитать) соответствующим образом значения переменной X для различных объектов: для более дорогой квартиры в случае наличия ремонта значение уменьшить, для более дешевой — увеличить. В этом и заключается суть предложенного механизма.

Корректировка/расчет значений переменной X, отличных от 0 (в случае наличия фактора у объекта) должны осуществляться исходя из того, на сколько в относительном выражении фактическая стоимость 1 кв.м. текущего объекта отличается от стоимости «базового» следующим образом:

где: Y_факт — фактическая цена 1 кв.м. оцениваемого объекта; K_АБС — абсолютная величина (предполагаемая) корректировки на влияние рассматриваемого аддитивного фактора.

Ниже в таблице представлены расчетные значения переменной Х, коэффициента k и абсолютные величины корректировок на «хороший ремонт» для нашего примера:

Таблица 1

Пример расчета корректировки на «ремонт»

Фактическая цена 1 кв.м. объекта (Yфакт)	Значение
	Переменная Х	Относит. кор-ка (kX)	Абсолют. кор-ка KАБС
«базовый» (40 т.р.)	1	1,1	4 000 руб.
более дорогой (49 т.р.)	0,889	1,0884	3 995 руб.
более дешевый (39 т.р.)	1,143	1,1151	4 027 руб.

Таким образом, логика формирования расчетной цены 1 кв.м. анализируемого объекта (Y) по модели не изменится, но с поправкой на то, что теперь фактор Х будет влиять непосредственно с величиной, описываемой коэффициентом k, лишь на объект с базовыми параметрами. Величина относительной корректировки (k^X) для объектов с различной ценой будет пересчитываться за счет изменения значений переменной Х, а величина итоговой абсолютной корректировки останется примерно на одном уровне. Причем неважно, запланирован ли данный уровень изначально или нет.

Однако в случае использования предложенного механизма есть определенная особенность: величина относительной корректировки, например на ремонт, рассчитывается исходя из фактической цены анализируемого объекта, т. е. рассматривается ситуация, когда фактическая цена складывается из суммы цены без учета ремонта и абсолютного значения корректировки на ремонт. При этом величина «теоретическая цена без учета ремонта» определяется исходя из величины параметра С, скорректированной на влияние присущих анализируемому объекту факторов. Таким образом в случае, если анализируемый объект характеризуется большим количеством индивидуальных параметров, и «расчетная цена без ремонта» по модели будет значительно отклоняться от теоретической, будет происходить искажение абсолютной величины корректировки на ремонт. То есть использование механизма наиболее эффективно при условии низкого значение ошибки расчетов.

2.    Особенности влияние величины параметра «базовая площадь» на коэффициенты модели

При исследовании рынка жилья с помощью предлагаемой методики, ввиду расчета коэффициентов с помощью МНК, можно столкнуться со следующей особенностью: параметры модели, т. е. величины некоторых итоговых коэффициентов, а соответственно, и корректировок, могут изменяться в зависимости от того, какие величины площадей выбраны в качестве базовых. При этом конечные результаты по моделям, после пересчета их через соответствующие коэффициенты, изменяться не будут [3].

В качестве основных изменяющихся параметров можно выделить: 1) величина параметра С — цена 1 кв.м.общего базового объекта; 2) корректировки, описывающие влияние фактора количества комнат; 3) корректировки, описывающие влияние материала стен, типа планировки (дома) и другие.

Общая выборка объектов может быть разделена по определенным факторам на группы, и оценка влияния «фактора площади» может осуществляться для каждой их них в отдельности. В таком случае для каждой группы определяется «свой» базовый объект. Можно сделать следующий вывод: изменение базовых площадей приводит к изменению всех параметров, описывающих ценообразующие факторы, по которым обусловлено деление выборки на данные группы.

При этом заметим, что разница в параметрах моделей будет выражаться лишь в абсолютных числовых значениях их коэффициентов. С «технической» точки зрения разницы никакой не будет, так как при расчете итоговых корректировок или стоимости анализируемого объекта в целом, итоговые результаты по моделям с разными параметрами получатся эквивалентными друг другу.

Рассмотрим в качестве примера 2 варианта модели, построенной на базе выборки из реальных данных по г. Уфа [4]. Оценка влияния фактора площади проводилась в комплексе для нескольких групп объектов исходя из следующих параметров (всего 8 групп): 1) количество комнат — 1, 2, 3 и 4; 2) тип дома (всего 2 типа) — 9–12-ти этажные панельные 80–90-х гг. постройки со стандартной и улучшенной планировкой, а также новые кирпичные дома с современной планировкой.

Общий «базовый» объект (параметр С) в модели обладает следующими характеристиками: 1-комнатная квартира, в панельном доме, не на первом этаже, с обычным ремонтом, с разной площадью — в зависимости от варианта.

Входные параметры для обоих вариантов модели отличаются друг от друга лишь значениями базовых площадей для описанных групп, которые приведены в табл. 2.

Таблица 2

Значения базовых площадей по группам объектов для двух вариантов модели

Кол-во комнат	1	2	3	4
Вариант 1	34 кв.м	45 кв.м	65 кв.м	92 кв.м
Вариант 2	36 кв.м	50 кв.м	72 кв.м	92 кв.м

Ниже в табл. 3 и 4 представлены значения приведенных выше коэффициентов уже из восстановленной к мультипликативному виду модели.

Таблица 3

Итоговые восстановленные значения коэффициентов модели (вариант 1)

Таблица 4

Итоговые восстановленные значения коэффициентов модели (вариант 2)

По значению корректировок из таблиц видно, что описанная выше особенность подтверждается — изменение величин базовых площадей ведет к изменению зависимых от них параметров модели. Рассмотрим изменение цены 1 кв.м. базового» объекта: во 2-м варианте она оказалась ниже, чем в 1-м. Теперь рассчитаем по представленной ранее схеме, на основе коэффициентов 1-го варианта модели, цену 1 кв.м.однокомнатной квартиры с площадью 36 кв.м. в панельном доме:

Как видим, результат получился идентичным результату из 2-го варианта. Данный факт свидетельствует о том, что разница в расчетной цене «базовых» объектов для разных вариантов модели возникает лишь из-за разницы в их площадях. При этом итоговые результаты разных вариантов модели при пересчете эквивалентны друг другу.

Таким образом, при проведении исследования необходимо на этапе обработки исходных данных четко определить величину базовых площадей для каждой из групп объектов исходя из условий и целей осуществления исследования.

Литература:

1.    Азнабаев А. М. Исследование ценообразования на рынке жилья (на примере г. Уфы) // Экономика и управление: научно-практический журнал. 2010. № 6. С.98.

2.    Сивец С. А. Построение и практическое применение многофакторной гибридной модели оценки доходной недвижимости // Вопросы оценки. 2001. № 4. С. 27–36.

3.    Азнабаев А. М. Определение влияния «Фактора площади» на стоимость объектов жилой недвижимости // Вестник Башкирского университета. 2010. Т. 15. № 4. С.1099.

4.    Азнабаев А. М. Анализ результатов исследования рынка жилой недвижимости г.Уфы в 2010г. на основе математической модели // Соврем. тенденции в экономике и управлении: новый взгляд: сборник материалов VI Международной научно-практ. конф. / Под общ. ред. С. С. Чернова. — Новосибирск: Изд-во НГТУ, 2010. С.165–169.