Для оптимизации структуры и свойствэпоксидного композита повышенной плотности для защиты от радиации [1…3] займемся построением множеств В.Парето. Воспользуемся полученными на основе математических методов планирования эксперимента аналитическими зависимостями средней плотности r, кг/м3, и предела прочности Rсж, МПа, на сжатие образцов 20´20´20 см:
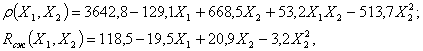
где X1, X2 — кодированные значения соответственно концентрации x1 пластификатора (в % от массы смолы) и степени наполнения x2(П:H по массе);x10 = 25, I1 = 25; x20 =1/7, I2Н = 5.
Следуя В.Парето, в общем случае из неформального анализа исключаются заведомо плохие варианты решений,что позволяетсократить множество исходных вариантов (здесь факторное пространство является двумерным). Пусть сделан некоторый выбор x* и предположим, что существует некоторый другой выбор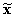
такой, что для всех критериев 
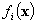имеют место неравенства
,
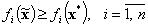причём хотя бы одно из неравенств — строгое (в рассматриваемом случае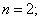 
, 
).
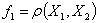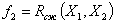Очевидно, что выбор 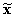предпочтительнее x*. Поэтому все векторыx*, удовлетворяющие последнему неравенству, можно сразу исключить из рассмотрения. Имеет смысл заниматься сопоставлением и подвергать неформальному анализу только те векторы x*, для которых не существует 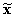такого, что для всех критериев удовлетворяются эти неравенства. Множество всех таких значений x* и называют множеством Парето, а вектор x* называютне улучшаемым вектором результатов (вектором Парето), если из 
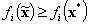для любого i следует 
.
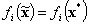Если цели являются двумя однозначнымифункциями (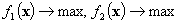
), то каждому допустимому значению переменной x отвечает одна точка на плоскости (f1, f2) (рис.1), и равенства
определяют параметрическое задание некоторой кривой abcd в этой плоскости. Участок bc, очевидно, не принадлежит множеству Парето, поскольку вместе с ростом f1 происходит и рост f2. Таким образом, на этом участке изменению переменной x отвечает одновременное увеличение обеих целевых функций и, следовательно, такие варианты решений должны быть сразу исключены из дальнейшего рассмотрения.
Из тех же соображений должен быть исключён и участок a¢b, поскольку для каждой его точки e найдётся точка, принадлежащая участку cd, в которой значения обеих функций f1 и f2 больше, чем в точке e. Так что принадлежать множеству Парето могут только участки aa¢ и cd, причём точка a¢ также должна быть исключена.
В теории принятия решений существует термин “принцип Парето”, заключающийся в том, что выбирать в качестве решения следует только тот вектор x, который принадлежит множеству Парето.
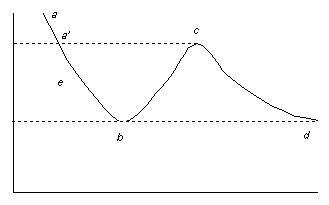
Рис. 1
Принцип Парето не выделяет единственного решения, он только сужает множество альтернатив. Окончательный выбор остаётся за лицом, принимающим решение. Построение множества Парето облегчает процедуру выбора решения.
Для случая двух критериев найдем решение задачи:
.
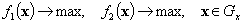Каждой точке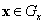 
соотношения 
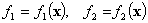ставят в соответствие некоторую точку Î Gf вплоскости критериев (рис. 2). Последние соотношения определяют отображение множества Gx на Gf. Множество Gf носит название множества достижимости, или множества предельных возможностей. Множество Парето представляет собой границы Gf. На рис. 2 множеством Парето будет дуга АDCВ.
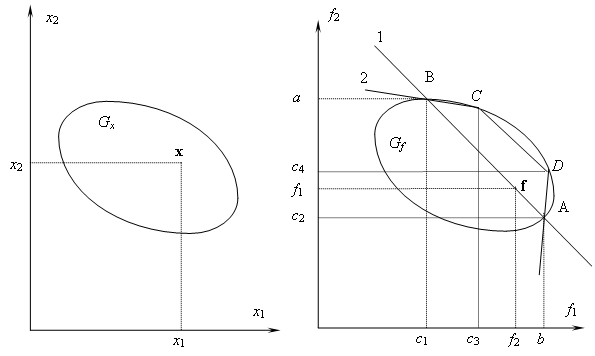
Рис. 2
Приближённое построение множества Парето сводится к последовательному решению задач математического программирования. Опишем одну из возможных схем расчёта. Зафиксируем желательные значения критериев f1и f2: f1 = c1, f2 = c2.
Значения c1 и c2 должны принадлежать множеству достижимости.
Решив две оптимизационные задачи:
I.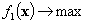 
, 
;
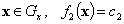II.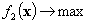 
, 
,
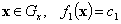определим точки А и В (рис. 2). Проведя через них прямую 1, получим простейшую аппроксимацию множества Парето. Для уточнения последнего можно определить ещё две точки — C и D, принадлежащие этому множеству и соответствующие решениям нижеследующих задач:
III. ,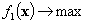 
;
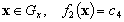IV. ,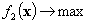 
.
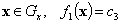Значения c3 и c4 также должны принадлежать множеству достижимости. Ломаная ADCB будет следующим приближением множества Парето. При
; 
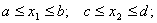
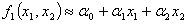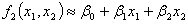
построение множества Парето сводится к последовательному решению следующих двух
задач линейного программирования:
1. Определить неотрицательные значения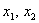 
, доставляющие максимум целевой функции 
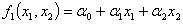при ограничениях
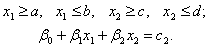
2. Определить неотрицательные значения , доставляющие максимум целевой функции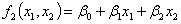 
при ограничениях
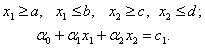
Решение этих задач производится с использованием метода штрафных функций Эрроу-Гурвица.
На основе экспериментальных данных в качестве области Gx принимался прямоугольник, соответствующий –1 £ X1 £ –0,6; 0,4 £ X2£ 0,8. При этом в области Gf (рис. 4):
3900 £ r £ 3950; 140 £ Rсж£ 150.
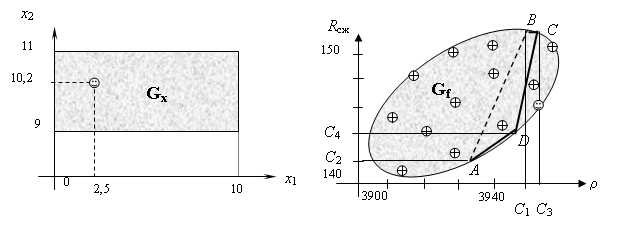
Рис. 3. Области Gx и Gf, множество Парето
На рисунке 3 множеству Парето в первом приближении соответствует отрезок AB (принято: с1= 3950; с2= 142); второе приближение — ломаная ADCB (с3= 3955; с4= 144).
Эффективность метода подтверждается приводимыми на рис. 4 линиями уровня r(X1,X2)= const(ветвь гиперболы), Rсж (X1, X2) = const(парабола) квадратичных моделей целевых функций, позволяющими в качестве оптимальных принять x1= 2,5; x2= 10,2.
Соответствующие им значения плотности и предела прочности:
r = 3955, Rсж = 145.
Получение информации о множестве Парето будет достаточным при решении и многих других аналогичных задач материаловедения.
Описанный способ применим и в случае большего числа переменных и частных критериев качества [4,5].
Рис. 4. Линии уровня r(X1, X2) = const, Rсж(X1, X2) = const
Литература:
1. Прошин А. П., Данилов А. М., Гарькина И. А., Королев Е. В., Смирнов В. А. Синтез строительных материалов со специальными свойствами на основе системного подхода / Известия ВУЗов. Строительство. — 2003. -№ 7.-С.43–47.
2. Будылина Е. А., Гарькина И. А., Данилов А. М., Пылайкин С. А. Подходы к многокритериальности сложных систем / «Молодой ученый. — № 6(53), 2013. — с.40–43.
3. Гарькина И. А., Данилов А. М., Петренко В. О. Проблема многокритериальности при управлении качеством сложных систем / Мир транспорта и технологических машин. № 2(41). 2013. –С.123–130.
4. Данилов А. М., Гарькина И. А. Методология проектирования сложных систем при разработке материалов специального назначения / Известия ВУЗов. Строительство. — 2011. -№ 1.-С.80–85.
5. Будылина Е. А., Гарькина И. А. Данилов А. М. Моделирование с позиций управления в технических системах / Региональная архитектура и строительство. № 2(16). 2013. — C. 138–143.
