Автомобили многоцелевого назначения достаточно широко эксплуатироваться в народном хозяйстве, промышленности, строительстве, а так же в военной сфере и имеют, несомненно, длительную перспективу развития. Этим и обусловлена необходимость в систематизации вопросов теории, конструирования и эксплуатации автомобилей многоцелевого назначения. Для специальных машин, работающих в сложных дорожно-климатических эксплуатационных условиях, а во многих случаях просто на бездорожье и в экстремальных природных и техногенных чрезвычайных ситуациях, производительность определяется их мобильностью. Для повышения скоростных характеристик, и характеристик проходимости, необходимо внедрять в электронную систему управления двигателем дополнительные алгоритмы работы двигателя и управления механизмами привода, а так же торможения колес. Следовательно, встает задача разработки различных вариантов алгоритма управления подачей топлива в двигатель, а так же управления торможением колес автомобилей многоцелевого назначения. [4, с. 24]
Исходные положения динамики движения буксующего эластичного колеса, обусловливают необходимость, для обеспечения требуемого уровня подвижности автомобилей многоцелевого назначения, подводить к колесу соответствующий его сцеплению с опорной поверхностью крутящий момент. Это будет способствовать ограничению буксования колеса в пределах, соответствующих наибольшему сцеплению с опорной поверхностью. [2, с. 276]
Следовательно, основной задачей предлагаемого способа является поддержание в процессе движения относительного буксования колес в узких пределах критического буксования dкр. В этом случае обеспечиваются оптимальные тяговые характеристики. Для этой цели необходимо в процессе движения регулировать момент, подводимый к ведущим колесам.
Ограничение при этом момента двигателя не всегда целесообразно, так как это обеспечит требуемый эффект только для буксующего колеса (снизит его буксование). Однако это не будет способствовать реализации возможностей колеса, имеющего большее сцепление с опорной поверхностью. Наиболее целесообразно использовать свойства симметричного дифференциала, распределяющего момент между колесами поровну. [3, с. 73–89]
Если буксование машины высокое, необходимо уменьшить подачу топлива. Это знание представим с помощью продукционного ЛПУ типа «если... то.».. следующим образом
«Если буксование машины высокое, то уменьшить подачу топлива». (1)
Выражение, стоящее после если, называется предпосылкой, условием, а выражение, стоящее после то, — заключением, операцией. Предпосылку и заключение описываем в виде соответствующего нечеткого отношения. В предпосылке нечетким знанием является «высокая», а в заключении должна присутствовать количественная характеристика слова «уменьшить», однако пока неясно, на сколько следует уменьшить подачу топлива [7]. Другими словами, в исходное выражение должны попасть знания о том, каково буксование машины в % и на сколько % следует уменьшить подачу топлива. При этом интерпретация с помощью нечеткого множества имеет следующий вид:
ВЫСОКОЕ = 0,1 | 40 + 0,5 | 50 + 0,7 | 60 + 0,9 | 70 + 0,95 | 80 + 1,0 | 90+1,0 | 100.(2)
Аналогично представляем уменьшение подачи топлива, в процентах от первоначального значения
УМЕНЬШИТЬ = 0,1 | 20 + 0,2 | 30 + 0,6 | 50 + 0,9 | 70 + 1,0 | 80 +1,0 | 90 +1,0 | 100.(3)
Таким образом, продукционное правило (1), представленное в словесной форме, выражается в виде двух нечетких множеств (2) и (3).
При проектировании системы ограничения буксования ведущих колес, используя знания о влиянии уменьшении подачи топлива в двигатель на ограничения буксования ведущих колес и получаемые реальные результаты, корректируем значения функции принадлежности до тех пор, пока система наилучшим образом не будет моделировать конкретную ситуацию.
Для проектирования следуем методике, описанной в [1], выполняем при этом следующие действия [5]:
1) вначале определяем значения методом вопросов и ответов;
2) затем выполняем операции и воссоздаем ситуацию из хронометрированных данных;
3) наконец, он корректируем значения функции, получая наилучшие результаты из экспериментов, имитирующих (моделирующих) данную ситуацию.
Значения функций принадлежности храним в базе данных приложения Fuzzylogic toolbox пакета расширения Matlab [9], содержащий инструменты для проектирования систем нечеткой логики [10]. Matlab является пакетом прикладных программ для решения задач технических вычислений и одноимённым языком программирования. Например, формулы типа (2) и (3) храним в виде одномерного файла. Таким образом, продукционные правила (1), которых может быть сколько угодно, будут накапливаться в базе знаний Matlab.
Лингвистические правила управления НК
Понятие «высокое буксование» на практике имеет различные оттенки: «довольно высокое буксование», «очень высокое буксование» и т. д. В процессе анализа информации и экспериментальных данных обнаружено, что
«Буксование машины довольно высокое». (4)
Записанную в виде ЛПУ информацию (4) можно представить с помощью нечеткого множества:
Довольно ВЫСОКОЕ = 0,5 | 60 + 0,9 | 70 + 1 | 80 + 0,8 | 90 + 0,2 | 100.(5)
Теперь требуется сделать заключение на основе двух продукционных правил:
«Если ВЫСОКОЕ буксование, то УМЕНЬШИТЬ подачу топлива».
«Довольно ВЫСОКОЕ буксование». (6)
Предпосылка «высокое» и наблюдение «довольно высокое» образуются путем сопоставления. Как известно, в четкой логике сопоставление не имеет смысла, поэтому никакого логического вывода сделать нельзя. В нечеткой логике ситуация складывается иная. Человек (водитель автомобиля многоцелевого назначения), исходя из продукционных правил (6), может сделать заключение, что следует «немного» уменьшить подачу топлива. То есть путем приближенного сопоставления правил (6) водитель (а в интеллектуальной системе — нечеткий контроллер) делает логически правильный нечеткий вывод:
«Если ВЫСОКОЕ, то УМЕНЬШИТЬ»
«Довольно ВЫСОКОЕ»______________________________
«Немного УМЕНЬШИТЬ». (7)
Существует более ста методов преобразования нечетких выводов на лингвистическом уровне в вычислительные схемы [6]. Применяем один из наиболее часто используемых на практике методов (рисунок 1). Здесь полное пространство предпосылок X — буксование машины в %, а полное пространство заключений Y — степени уменьшения подачи топлива в %.
Используя формулы (2) и (3), нечеткое продукционное ЛПУ (1) изобразим графически, как показано на рисунке 1, а. Для упрощения рассуждений обозначим через А нечеткое множество «Высокое» в предпосылке X и через В — нечеткое множество «Уменьшить» в предпосылке Y.
Нечеткое множество «Довольно высокое» в данных наблюдения X обозначим через А' и представим, как показано на рисунке 1, б.
На рисунке 1, в графически изображен процесс классического нечеткого вывода.
Значение А ∩ А' получено в результате приближенного сопоставления предпосылки правила А и данных наблюдения А'.
Затем рассмотрим максимальное значение а как некую меру сопоставления А ∩ А', выполним редукцию по этой мере заключения В в правиле и получим результат вывода В (рисунок 1, в) качестве способа редукции В выбрано отсечение по мере сопоставления а. На рисунке aY означает, что
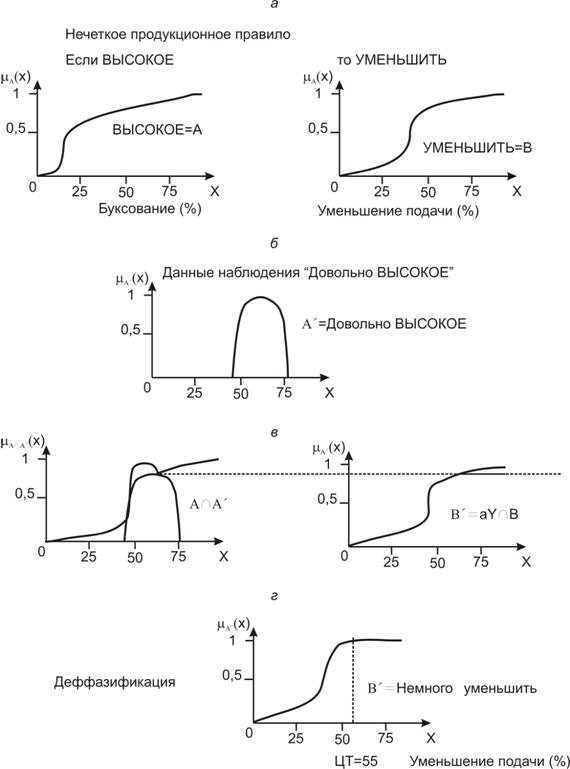
Рис. 1. Нечеткий вывод по правилам
Для текущих данных наблюдения А' (Довольно ВЫСОКОЕ) в результате применения правила А → В (Если ВЫСОКОЕ, то УМЕНЬШИТЬ) получаем В' (Немного УМЕНЬШИТЬ). Здесь результат вывода В' является нечетким множеством в Y, как показано на рисунке 1, г. Однако на этом этапе пока еще нельзя принять окончательное четкое решение по управлению подачей топлива.
Для получения четкого решения на основе функции принадлежности μВ'(х) для В необходимо еще извлечь для каждой точки в Y значения — провести процесс дефаззификации [8]. Процесс дефаззификации не будет рассмотрен в данной статье, так как является отдельным разделом диссертационной работы. Поэтому на данном этапе статья считается завершенной.
Литература:
1. Агейкин, Я. С. Вездеходные колесные и комбинированные движители [Текст] / Я. С. Агейкин -М.: Машиностроение, 1972. — 184 с.
2. Асаи К. Прикладные нечеткие системы // К. Асаи, Д. Ватада, С. Иваи и др.: Пер. с япон. М.: Мир, 1993. 342 с.
3. Келлер А. В. Принципы и методы распределения мощности между ведущими колесами автомобильных базовых шасси: Монография [Текст] / А. В. Келлер, И. А. Мурог — Челябинск, 2009–224 с.
4. Кристальный, С. Р. Критерии оценки автотранспортных средств, оснащённых противобуксовочными системами [Текст] / Дис.... канд. техн. наук: 05.05.03. — Л., 2007. — 269 с.
5. Тарасик, В. П. Интеллектуальные системы управления автотранспортными средствами [Текст] / В. П. Тарасик, С. А. Рынкевич. —Мн.: УП «Технопринт», 2004. — 512 с.
6. Торопов, А. Н. Математическая модель маршрута движения автомобилей многоцелевого назначения [Текст] / А. Н. Торопов, А. В. Келлер, А. Ю. Кокшин // Многоцелевые гусеничные и колесные машины: актуальные проблемы пути их решения: Материалы международной научно-технической конференции, посвященной 100-летию со дня рождения М. Ф. Балжи- ЮУрГУ — Челябинск., 2008. с. 60–67
7. Торопов, А. Н. О рациональном передаточном отношении межосевого дифференциала транспортного средства [Текст] / А. Н. Торопов, А. В. Келлер, Р. Ю. Хмара, Д. И. Шарафутдинов. // Современные тенденции развития транспортного машиностроения: Сборник статей X международной научно — технической конференции. — Пенза, 2005. c. 51–53
8. Шафиков, Д. Р. Обоснование выбора вида функции принадлежности при разработке нечеткого алгоритма ограничения буксования [Текст] / Д. Р. Шафиков, А. В. Келлер. // Сборник статей IV Научной конференции аспирантов и докторантов.- Челябинск, 2012. с. 43–47.
9. Информационный центр Mathworks. 1994–2013 The MathWorks, Inc URL: http://www.mathworks.com/help/matlab/learn_matlab/product-description.html (дата обращения: 15.02.2012)
10. Обзор центра компетенции Mathworks. Продукты и сервисы. 1994–2013 The MathWorks, Inc URL: http://sl-matlab.ru/products/fuzzy-logic-toolbox.html (дата обращения: 17.01.2012)







