1. Введение
Задача прогнозирования финансовых временных рядов была и остается актуальной, поскольку предсказание является необходимым элементом любой инвестиционной деятельности, ведь сама идея инвестирования — вложения денег с целью получения дохода в будущем — основывается на идеи прогнозирования будущего. В последнее время, когда стали доступны мощные средства сбора и обработки информации, задача прогнозирования финансовых временных рядов также становиться и одной из самых популярных задач для практического применения различных Data Mining методов [1]. Широкое применение Data Mining методов в данной области обусловлено наличием в большинстве временных рядов сложных закономерностей, которые не обнаруживаются линейными методами.
Однако практическое применение Data Mining методов для прогноза финансовых временных рядов сталкивается с проблемой нестационарности этих рядов. Закономерности развития финансовых рядов постоянно меняются, причем, как показывает практика, эти изменения могут происходить очень быстро. В результате успех или неудача при использовании прогнозирующих систем, обученных на исторических данных, во многом зависит от того, будет ли будущая динамика ряда соответствовать той динамики, которая была на обучающем множестве, или нет.
Зачастую для преодоления нестационароности финансовых данных предлагается регулярно переобучать прогнозирующие системы по мере поступления новых данных. Однако очевидным недостатком данного метода является его запаздывание: к тому моменту, когда в обучающем множестве накопиться достаточное количество новых данных, чтобы новая динамика ряда нашла отражение в закономерностях системы, эта динамика может либо уже закончиться, либо система может успеть дать неприемлемо большое количество ложных прогнозов. Таким образом, возникает проблема того, как определить, применима ли прогнозирующая система к текущей ситуации или нет.
Для решения этой проблемы нами предлагается использовать реляционный подход к извлечению знаний [1–2]. В рамках данного подхода нами была разработана технология предсказания финансовых временных рядов, использующая механизм проверки применимости полученных прогнозов к текущей ситуации. Технология заключается в том, что параллельно с обнаружением закономерностей, предсказывающих будущие значения ряда, обнаруживать также высоковероятные закономерности, описывающие динамику ряда на обучающем интервале, чтобы в дальнейшем, по нарушениям этих закономерностей, определять, соответствует ли текущая ситуация обучающему интервалу или нет. Мы исходим из предположения, что высоковероятные закономерности, описывающие динамику ряда, определяют его нормальное состояние, а нарушение этих закономерностей — аномальное: резкую смену тренда при выходе каких-либо новостей, обвал на рынке и т. д. Если текущая ситуация не соответствует обучающему интервалу, т. е. если произошло нарушение в динамике ряда, то следует воздержаться от применения закономерностей, предсказывающих будущие значения ряда, поскольку при их обнаружении такие ситуации не были учтены и велика вероятность получения ложного прогноза.
Важной особенностью предлагаемого подхода является возможность обнаружения таких признаков нарушения динамики, которые не встречались ранее на обучающей выборке. Для обнаружения признаков нарушения динамики не требуется наличия обучающего материала, т. е. известных примеров нарушений в динамике ряда, как это требуется существующими Data Mining методами.
2. Метод обнаружения вероятностных закономерностей
Предлагаемый нами метод позволяет для заданного класса гипотез 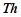 обнаружить на данных множество вероятностных закономерностей в виде логических правил вида
обнаружить на данных множество вероятностных закономерностей в виде логических правил вида
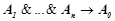
где 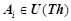 ,
, 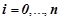 — литеры,
— литеры, 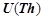 — множество всех литер.
— множество всех литер.
В работах [3–5] нами был предложен язык описания классов гипотез, который позволил разработать интерактивную систему задания классов гипотез, проверяемых на данных, и реализовать её в системе «Discovery».
Алгоритм поиска закономерностей основан на методологии семантического вероятностного вывода [1–2], который позволяет находить все вероятностные закономерности вида с максимальной вероятностью предсказывающие целевую литеру 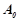 . Отличительной особенностью семантического вероятностного вывода является использование понятия вероятностной закономерности [1–2], которое звучит следующим образом. Правило
. Отличительной особенностью семантического вероятностного вывода является использование понятия вероятностной закономерности [1–2], которое звучит следующим образом. Правило 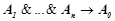 является вероятностной закономерностью, если для любого правила
является вероятностной закономерностью, если для любого правила 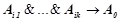 , такого что
, такого что 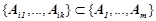 , условная вероятность
, условная вероятность 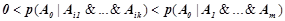 .
.
Для реализации семантического вероятностного вывода был разработан алгоритм направленного перебора правил [3,5], позволяющий существенно сократить пространство поиска. Суть алгоритма заключается в последовательном наращивании условной части правил с проверкой выполнимости условий вероятностной закономерности. Сокращение перебора осуществляется за счет использования эвристики, которая заключается в том, что, начиная с момента, когда длина условной части правил достигает некоторой заданной величины, алгоритм начинает последовательно наращивать условные части только тех правил, которые являются вероятностными закономерностями.
Вероятностные неравенства, входящие в определение вероятностной закономерности, проверяются на данных с использованием статистических критериев [4].
3. Метод обнаружения нарушений динамики временного ряда
Для обнаружения нарушений динамики временного ряда нами был разработан следующий метод, основанный на идее обнаружения аномальных событий [6–7].
1. Сформулировать вид гипотез 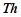 , описывающий нормальную динамику временного ряда.
, описывающий нормальную динамику временного ряда.
2. На анализируемом временном периоде обнаружить множество вероятностных закономерностей  для заданного вида гипотез
для заданного вида гипотез 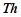 , предсказывающих все возможные литеры из
, предсказывающих все возможные литеры из 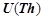 . Для этого необходимо последовательно брать каждую литеру из
. Для этого необходимо последовательно брать каждую литеру из 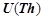 в качестве целевой и при помощи описанного выше метод находить множество предсказывающих её закономерностей.
в качестве целевой и при помощи описанного выше метод находить множество предсказывающих её закономерностей.
3. Среди обнаруженного множества закономерностей 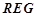 отобрать множество высоковероятных закономерностей
отобрать множество высоковероятных закономерностей 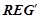 , описывающих нормальную динамику временного ряда. Для этого необходимо зафиксировать некоторый порог
, описывающих нормальную динамику временного ряда. Для этого необходимо зафиксировать некоторый порог 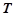 ,
, 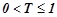 , к примеру,
, к примеру, 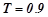 . Если
. Если 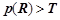 , где
, где 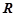 — правило из
— правило из 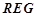 , то добавить правило
, то добавить правило 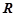 в множество
в множество 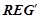 .
.
4. Сформировать множество закономерностей 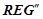 , описывающих нарушения динамики временного. Для этого необходимо для каждого правила
, описывающих нарушения динамики временного. Для этого необходимо для каждого правила 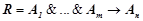 из
из 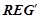 взять его отрицание
взять его отрицание 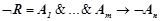 . Конъюнкция
. Конъюнкция 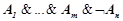 будет являться признаком нарушения динамики ряда, а правило
будет являться признаком нарушения динамики ряда, а правило 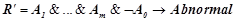 будет прогнозировать нарушение динамики с вероятностью
будет прогнозировать нарушение динамики с вероятностью 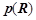 . Полученное правило
. Полученное правило 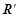 необходимо добавить в множество
необходимо добавить в множество 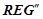 .
.
4. Технология прогнозирования финансовых временных рядов
Используя описанные выше методы, нами предлагается следующая технология прогнозирования финансовых временных рядов.
1. Сформулировать вид гипотез 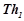 . На обучающем временном периоде
. На обучающем временном периоде 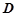 обнаружить множество вероятностных закономерностей
обнаружить множество вероятностных закономерностей 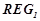 заданного вида гипотез
заданного вида гипотез 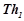 , предсказывающих дальнейшую динамику временного ряда, к примеру, увеличение или уменьшение цены, либо достижение ценой определенного уровня и т. п. Полученное множество закономерностей
, предсказывающих дальнейшую динамику временного ряда, к примеру, увеличение или уменьшение цены, либо достижение ценой определенного уровня и т. п. Полученное множество закономерностей 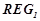 будет составлять основу прогнозирующей системы.
будет составлять основу прогнозирующей системы.
2. Сформулировать вид гипотез 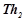 , описывающий динамику временного ряда на обучающем периоде
, описывающий динамику временного ряда на обучающем периоде 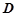 . На том же обучающем временном периоде
. На том же обучающем временном периоде 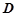 обнаружить множество закономерностей
обнаружить множество закономерностей 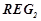 , заданного вида гипотез
, заданного вида гипотез 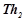 , прогнозирующих нарушения динамики временного ряда.
, прогнозирующих нарушения динамики временного ряда.
3. При прогнозировании использовать предсказания, полученные по закономерностям 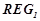 только в том случае, если степень отклонения в текущей динамике ряда меньше заданного порога, в противном случае считать, что текущая динамика ряда не соответствует обучающему периоду, и прогноз отсутствует. Степень отклонения в динамике ряда рассчитывается по прогнозам закономерностей
только в том случае, если степень отклонения в текущей динамике ряда меньше заданного порога, в противном случае считать, что текущая динамика ряда не соответствует обучающему периоду, и прогноз отсутствует. Степень отклонения в динамике ряда рассчитывается по прогнозам закономерностей 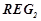 следующим образом
следующим образом 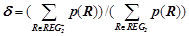 , где
, где 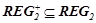 — множество закономерностей из
— множество закономерностей из 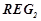 , условная часть которых выполнена в текущей ситуации.
, условная часть которых выполнена в текущей ситуации.
5. Пример разработки торговой системы
Продемонстрируем преимущество описанной технологии предсказания финансовых временных рядов на примере разработке торговой системы, предсказывающей курс акций ГМК «Норильский Никель». На рисунке 1 приведен график, отражающий динамику цен закрытия часа акций ГМК «Норильский Никель» на фондовой бирже ММВБ за период с 23 августа 2006 г. по 27 февраля 2009 г. Приведенные данные интересны тем, что достаточно продолжительный возрастающей тренд заканчивается резким обвалом курса в ноябре 2007 г. с последующей неоднократной сменой динамики ряда.
На примере данного финансового инструмента покажем, каким образом использование технологии обнаружения признаков нарушения динамики ряда позволяет уменьшить количество ложных прогнозов. Для этого мы специально выбрали обучающее множество, включающее период возрастающего тренда с 23 августа 2006 г. по 31 июля 2007 г. (выделенный на Рис. 1 штриховкой). Построим на данном обучающем периоде две торговые системы: первую — без использования указанной технологии, а вторую — с использованием. Затем посмотрим, как поведут себя обе системы после 31 июля 2007 г. при резкой смене динамики временного ряда.
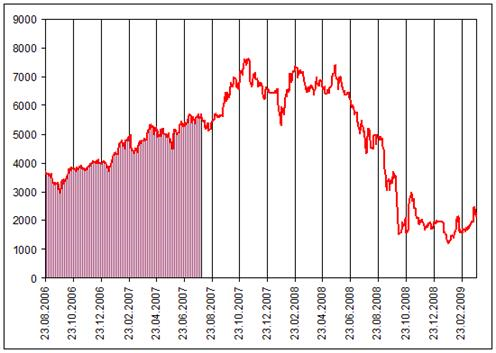
Рис. 1. Динамика цен ГМК «Норильский Никель»
Основой обоих торговых систем являются вероятностные закономерности, обнаруженные на обучающем периоде и предсказывающие рост или падение стоимости акций на пять часов вперед. Для обнаружения закономерностей нами был использован простой класс гипотез 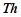 , сравнивающий между собой цены закрытия последних пяти часов с учетом текущего времени и дня недели.
, сравнивающий между собой цены закрытия последних пяти часов с учетом текущего времени и дня недели.
Первая торговая система основывается на следующем простом правиле открытия позиций. Если закономерности прогнозируют рост цены, то предлагается открыть позицию на покупку и держать ее пять часов. Если закономерности прогнозируют падение цены, то надо открыть позицию на продажу и держать ее пять часов. Если при этом ранее была открыта противоположная позиция, то надо её предварительно закрыть, а если была уже открыта аналогичная позиция, то надо продлить срок её удержания ещё на пять часов.
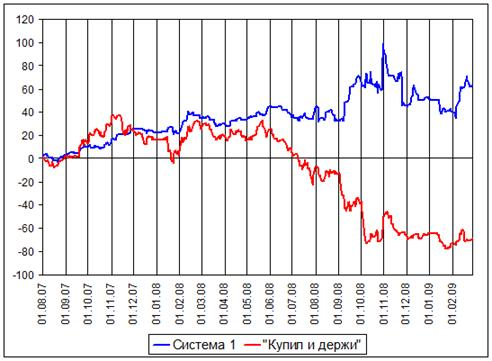
Результаты работы первой торговой системы на периоде с 1 августа 2007 г. по 27 февраля 2009 г. приведены на Рис. 2 и в Таблице 1. На Рис. 2 приведен график доходности системы в сравнении с доходностью при пассивном инвестировании (стратегия «купил и держи»), а в Таблице 1 представлены показатели финансовой эффективности системы. При детальном анализе графика доходности можно заметить, что система хорошо работает на периодах роста цены, т. е. когда динамика ряда соответствует динамике обучающего периода, и терпит убытки на периодах падения и бокового движения цен.
Рис. 2. Доходность первой системы в сравнении со стратегией «купил и держи».
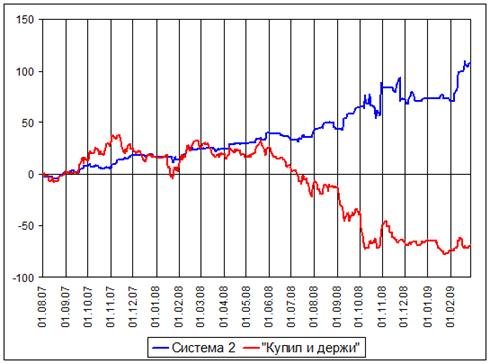
Рис. 3. Доходность второй системы в сравнении со стратегией «купил и держи».
Для второй торговой системы мы, при помощи метода обнаружения нарушений динамики, для указанного обучающего периода нашли множество правил, прогнозирующих нарушение динамики ряда. Для обнаружения этих правил мы, для простоты, использовали тот же самый класс гипотез 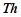 . Далее, в соответствии с описанной выше технологией прогнозирования, мы использовали прогнозы о росте или падении цен для открытия позиций только в тех случаях, когда степень отклонения динамики ряда была меньше заданного порога. В остальном правила открытия и закрытия позиций были такими же, как и у первой системы.
. Далее, в соответствии с описанной выше технологией прогнозирования, мы использовали прогнозы о росте или падении цен для открытия позиций только в тех случаях, когда степень отклонения динамики ряда была меньше заданного порога. В остальном правила открытия и закрытия позиций были такими же, как и у первой системы.
Результаты работы второй торговой системы на периоде с 1 августа 2007 г. по 27 февраля 2009 г. приведены на Рис. 3 и в Таблице 1. Как видно по результатам работы, использование технологии обнаружения признаков нарушения динамики ряда позволило отфильтровать ложные сигналы, что привело существенному росту процента прибыльных сделок и сократило максимальную просадку счета почти в два раза. График доходности системы также стал более плавным и стабильным.
Таблица 1
Сравнение финансовых показателей торговых систем
|
Показатель |
Система 1 |
Система 2 |
|
Доходность |
63.44 % |
108.27 % |
|
Процент прибыльных сделок |
51.91 % |
59.56 % |
|
Максимальная просадка счета |
-41.79 % |
-25.69 % |
Приведем несколько примеров обнаруженных закономерностей, соответствующих нормальной динамике ряда на обучающем периоде, и полученных на их основе правил, предсказывающих нарушение этой динамики.
1. Закономерность нормальной динамики:
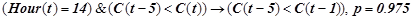 .
.
Правило, предсказывающее нарушение:
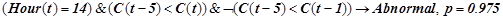 .
.
2. Закономерность нормальной динамики:
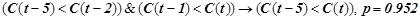 .
.
Правило, предсказывающее нарушение:
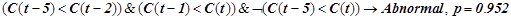 .
.
3. Закономерность нормальной динамики:
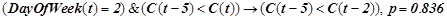 .
.
Правило, предсказывающее нарушение:
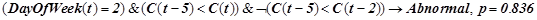 .
.
Здесь 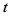 — текущий момент времени,
— текущий момент времени, 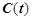 — значение временного ряда в момент времени
— значение временного ряда в момент времени 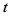 ,
, 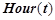 — текущий час,
— текущий час, 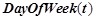 — текущий день недели (1 — понедельник, 2 — вторник и т. д.),
— текущий день недели (1 — понедельник, 2 — вторник и т. д.), 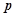 — условная вероятность правила.
— условная вероятность правила.
В полученных закономерностях можно проследить следующую тенденцию в поведении ряда: если ряд растет на некотором промежутке времени, то он растет на нем достаточно непрерывно. Эта особенность поведения полностью соответствует растущему тренду, который наблюдается на всем обучающем периоде. В тоже время максимальная частота нарушения этих закономерностей наблюдается на отрезках бокового тренда, т. е. как раз тогда, когда поведение ряда существенно отличается от поведения на обучающем интервале.
6. Заключение
В данной работе мы на примере финансовых временных рядов показали, каким образом использование технологии обнаружения нарушений динамики временного ряда позволяет улучшить качество прогнозирования нестационарных процессов. Однако имеются и другие возможности для эффективного использования указанной технологии, а именно:
1. В качестве предвестника существенного изменения динамики ряда. Данная возможность имеет большое значение для определения начала кризисных явлений на финансовых рынках. Если частота и количество нарушений начинает существенно возрастать, то это может свидетельствовать об изменении закономерности развития процесса и служить предвестником критических явлений на финансовых рынках. Из-за различной информированности участников рынка реакция на события, способные существенно изменить динамику рынка, приходит не сразу и имеет лавинообразный характер. Используя предложенную технологию можно отследить начало этих изменений и раньше на них отреагировать.
2. Для выбора предиктора среди набора предикторов, который в наибольшей степени соответствует текущей динамики ряда. Предположим, что у нас имеется набор предикторов, обученных на различных участках временного ряда. Эти участки могут быть специально подобраны таким образом, чтобы каждый из них содержал вполне определенную динамику ряда. Для прогноза выбирается тот предиктор, обучающий интервал которого более всех остальных соответствует текущей динамике ряда. Для определения соответствия можно, к примеру, использовать приведенный выше показатель степени отклонения в динамике ряда. Очевидно, что от выбранного таким образом предиктора можно ожидать более точного прогноза. В результате можно добиться существенно лучшего качества прогнозирования по сравнению с каждым отдельным предиктором из заданного набора.
Литература:
2. Витяев Е. Е. Извлечение знаний из данных. Компьютерное познание. Модели когнитивных процессов. — Новосибирск: НГУ, 2006. — 293 с.
3. Демин А. В., Витяев Е. Е. Реализация универсальной системы извлечения знаний «Discovery» и ее применение в задачах финансового прогнозирования // Информационные технологии работы со знаниями: обнаружение, поиск, управление. — Новосибирск, 2008. — Вып. 175: Вычислительные системы. — С. 3–47.
4. Демин А. В., Витяев Е. Е. Метод предсказания в языке первого порядка // Информационные технологии работы со знаниями: обнаружение, поиск, управление. — Новосибирск, 2008. — Вып. 175: Вычислительные системы. — С. 57–88.
5. Демин А. В., Витяев Е. Е., Полоз Т. Л. Реализация универсальной системы извлечения знаний «Discovery» и ее применение в задачах медицинской диагностики // Труды Всероссийская конференция с международным участием «Знания — Онтологии — Теории», Том 1, Новосибирск, 2007. — С. 63–70.
6. Витяев Е. Е., Ковалерчук Б. К., Федотов А. М., Барахнин В. Б., Белов С. Д., Дурдин Д. С., Демин А. В. Обнаружение закономерностей и распознавание аномальных событий в потоке данных сетевого трафика // Вестник НГУ, Информационные технологии. — 2008. — Т. 6. — Вып. 2. — С. 57–68.
7. Kovalerchuk B., Vityaev E., Holtfreter R. Correlation of Complex Evidence in Forensic Accounting Using Data Mining // Journal of Forensic Accounting 1524–5586. — Vol.VIII. — R. T. Edwards, Inc., 2007. — pp. 53–88.
[1] Работа выполнена при финансовой поддержке интеграционного проекта СО РАН № 136, интеграционного проекта РАН № 15/10 и гранта РФФИ № 11–07–0388-а.