Как известно, что некоторые актуальные задачи, в частности, задачи квантовой механики, статистической механики и гидродинамики сводятся к исследованию спектральных свойств обобщенной модели Фридрихса [1,2]. Поэтому изучение дискретного спектра обобщенной модели Фридрихса играет важную роль в современной математической физике.
В настоящей работы рассматривается (ограниченный и самосопряженный) обобщенный модель Фридрихса 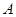 с возмущением ранга не более чем 4. Отметим, что оператор
с возмущением ранга не более чем 4. Отметим, что оператор 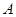 ассоциирован с системой не более чем двух квантовых частиц на
ассоциирован с системой не более чем двух квантовых частиц на 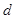 -мерной решетке. Найден явный вид существенного и дискретного спектра оператора
-мерной решетке. Найден явный вид существенного и дискретного спектра оператора 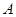 .
.
Пусть 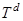 -
- 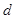 -мерный тор, т. е. куб
-мерный тор, т. е. куб 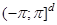 — с соответствующим отождествлением противоположных граней,
— с соответствующим отождествлением противоположных граней, 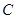 — одномерное комплексное пространство, а
— одномерное комплексное пространство, а 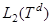 — гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на
— гильбертово пространство квадратично-интегрируемых (комплекснозначных) функций, определенных на 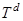 .
.
Обозначим через 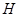 прямую сумму пространств
прямую сумму пространств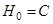 и
и 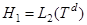 , т. е.
, т. е. 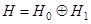 . Пространство
. Пространство 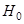 и
и 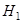 называется нолчастичном и одночастичном подпространством фоковского пространства
называется нолчастичном и одночастичном подпространством фоковского пространства 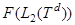 над
над 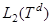 , соответственно.
, соответственно.
Рассмотрим обобщенную модель Фридрихса 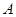 действующую в гильбертовом пространстве
действующую в гильбертовом пространстве 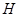 как
как 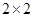 блочно операторная матрица
блочно операторная матрица
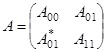 ,
,
где операторы 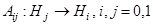 определяются по правилам
определяются по правилам
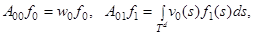
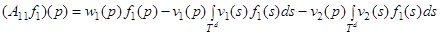 (1).
(1).
Здесь 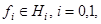
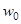 - фиксированное вещественное число,
- фиксированное вещественное число, 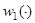 и
и 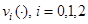 — вещественно-непрерывные функции на
— вещественно-непрерывные функции на 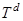 , а
, а 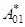 сопряженный оператор к
сопряженный оператор к 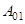 .
.
Легко можно проверить, что при этих предположениях оператор 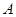 ограничен и самосопряжён в гильбертовом пространстве
ограничен и самосопряжён в гильбертовом пространстве 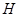 . Надо отметить, что всякий линейный ограниченный оператор в
. Надо отметить, что всякий линейный ограниченный оператор в 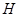 всегда записывается как
всегда записывается как 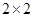 блочно операторная матрица.
блочно операторная матрица.
Оператор 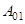 называется оператором уничтожения, а оператор
называется оператором уничтожения, а оператор 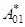 называется оператором рождения [4].
называется оператором рождения [4].
Обозначим через 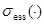 и
и 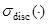 соответственно существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
соответственно существенный спектр и дискретный спектр ограниченного самосопряженного оператора.
Пусть оператор 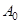 действует в
действует в 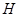 как
как
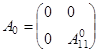 ,
,
где 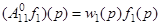 .
.
Оператор возмущения 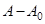 оператора
оператора 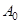 является самосопряженным оператором ранга не более чем 4. Следовательно, из известной теоремы Г. Вейля [3] о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора
является самосопряженным оператором ранга не более чем 4. Следовательно, из известной теоремы Г. Вейля [3] о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр оператора 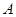 совпадает с существенным спектром оператора
совпадает с существенным спектром оператора 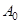 . Известно, что
. Известно, что 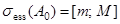 , где числа
, где числа 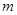 и
и 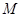 определяются следующим образом:
определяются следующим образом:
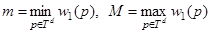 .
.
Из последних фактов следует, что
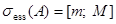 . (1)
. (1)
Определим регулярную в 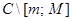 функции
функции
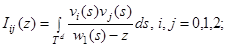
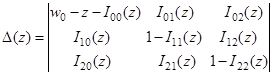 .
.
Следующая теорема устанавливает связь между собственными значениями оператора 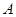 и нулями функции
и нулями функции 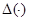 .
.
Теорема 1. Для дискретного спектра оператора 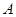 имеет место равенство
имеет место равенство
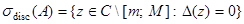 .
.
Доказательство. Чтобы доказать теоремы достаточно показать, что оператор 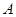 имеет собственное значение
имеет собственное значение 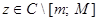 тогда и только тогда, когда
тогда и только тогда, когда 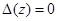 .
.
Действительно. Пусть число 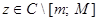 — есть собственное значение оператора
— есть собственное значение оператора 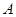 и пусть
и пусть 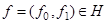 — соответствующая собственная вектор-функция. Тогда
— соответствующая собственная вектор-функция. Тогда 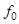 и
и 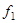 удовлетворяют следующую систему уравнений
удовлетворяют следующую систему уравнений
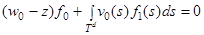 ;
;
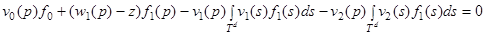 . (2)
. (2)
В силу равенства (1) для любых 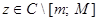 и
и 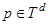 имеет место соотношение
имеет место соотношение 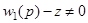 . Из второго уравнения системы (2) для
. Из второго уравнения системы (2) для 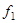 имеем
имеем
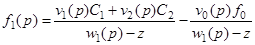 , (3)
, (3)
где
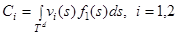 . (4)
. (4)
Подставляя выражение (3) для 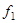 в первое уравнение системы (2) и равенству (4) получим, что система уравнений (2) имеет ненулевое решение тогда и только тогда, когда система уравнений
в первое уравнение системы (2) и равенству (4) получим, что система уравнений (2) имеет ненулевое решение тогда и только тогда, когда система уравнений
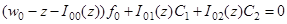 ;
;
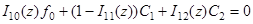 ;
;
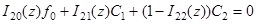 ;
;
имеет ненулевое решение, т. е. когда 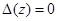 . Теорема 1 доказана.
. Теорема 1 доказана.
Согласно теореме 1 функция 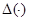 обладает характеристическим свойством определителя Фредгольма. По этой причине мы назовём её определителем Фредгольма, ассоциированный с оператором
обладает характеристическим свойством определителя Фредгольма. По этой причине мы назовём её определителем Фредгольма, ассоциированный с оператором 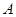 .
.
Рассмотрим некоторые частные случаи:
I. Из теоремы 1 видно, что если функции 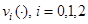 удовлетворяет условие
удовлетворяет условие
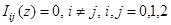 (5)
(5)
при всех 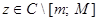 , то дискретный спектр оператора
, то дискретный спектр оператора 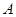 совпадает с объединением дискретных спектров операторов
совпадает с объединением дискретных спектров операторов
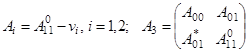 ,
,
где
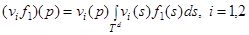 ,
,
т. е.
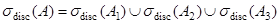 .
.
Из определения операторов 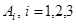 видно, что они имеют более простую структуру чем
видно, что они имеют более простую структуру чем 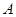 , причем операторы
, причем операторы 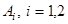 имеют по одному простых собственных значений, лежащих левее
имеют по одному простых собственных значений, лежащих левее 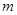 , а оператор
, а оператор 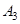 имеет две простых собственных значений, один из них лежать левее
имеет две простых собственных значений, один из них лежать левее 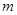 , а второе правее
, а второе правее 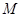 .
.
Положим
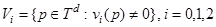 .
.
Отметим, что если мера Лебега множества 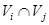 равно нулю при всех
равно нулю при всех 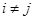 ,
, 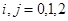 , то выполняется условие (5).
, то выполняется условие (5).
II. Если 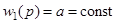 , то обозначая
, то обозначая
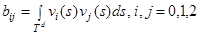 ,
,
имеем, что 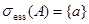 (т. е. число
(т. е. число 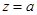 является бесконечнократным собственным значением оператора
является бесконечнократным собственным значением оператора 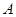 ) и
) и
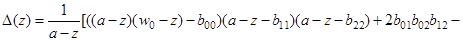
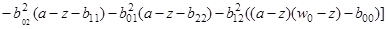 .
.
Видно, что в этом случае 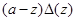 является полином четвертого порядка, и следовательно, оно имеет не более чем четыре (с учетом кратности) вещественных нулей отлично от
является полином четвертого порядка, и следовательно, оно имеет не более чем четыре (с учетом кратности) вещественных нулей отлично от 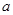 . По теореме 1 это означает, что оператор
. По теореме 1 это означает, что оператор 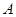 имеет не более чем четыре (с учетом кратности) собственных значений, лежащих вне существенного спектра.
имеет не более чем четыре (с учетом кратности) собственных значений, лежащих вне существенного спектра.
Литература:
1. Л. Д. Фаддеев. О модели Фридрихса в теории возмущений непрерывного спектра // Труды Математического Института АН СССР, 1964, Т. 73, С. 292–313.
2. Р. А. Минлос, Я. Г. Синай. Исследование спектров стохастических операторов, возникающих в решетчатых моделях газа // Теоретическая и математическая физика, 1979, Т. 2, № 2, С. 230–243.
3. М. Рид, Б. Саймон. Методы современной математической физики // Т. 4, Анализ операторов, М.: Мир, 1982.
4. К. О. Фридрихс. Возмущения спектра операторов в гильбертовом пространстве. М.: Мир, 1972.







