Популярные демо-генетические модели в случае, когда вредитель, в частности, стеблевой кукурузный мотылек, при температуре воздуха свыше 20 градусов утрачивают способность перемещаться самостоятельно и переносятся теплым течением воздуха [1].
Ключевые слова: единственность, вредитель, трансгенные агрокультуры.
Рассмотрим модель адаптации вредителей к трангсенным агрокультурам при различных типах таксиса, учитывающую диффузию и конвекцию [2]:
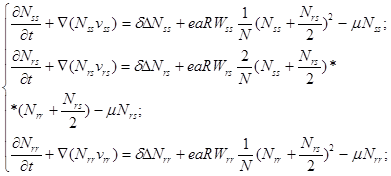(1)
где KR- емкость среды, dR, - коэффициент диффузии растительного ресурса,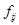 
определяют пропорции распределения потомства вредителя по трем рассматриваемым генотипам ij, N - внешняя нормаль к границе 
, 
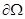- ареал вредителя; 
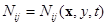- плотность генотипа ij в точке 
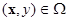в момент времени t(
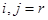или s), 
, 
, 
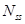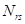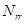— плотности соответствующих генотипов вредителя; 
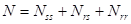- общая плотность популяции.
Активность вредителей определяется суммой плотностей двух видов вредителей в активном и пассивном состоянии соответственно: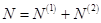 
.
Пусть на площади 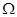находятся 
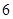типов вредителей (по 3 на каждый вид таксиса), которые в точке 
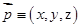в момент времени 
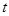имеют концентрации 
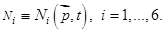Будем рассматривать следующую модель распространения вредителей:
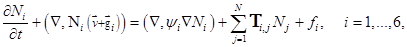(2)
где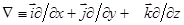 
− оператор набла; 
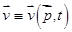− скорость макроскопического движения жидкости; 
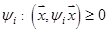− тензор диффузии вредителей 
; 
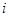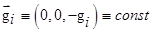− скорость гравитационного осаждения;
− матрица взаимного распределения вредителей;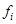 
− функция мощности потоков .
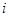Слагаемые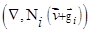 
в левой части уравнений (2) описывают конвекцию вредителей: их перенос под действием течения воздуха и силы тяжести [3]. Введем поле скоростей макроскопического движения вредителей: 
Слагаемые в правой части уравнений (2) описывают диффузию примесей и их преобразование из одного типа в другой.
Система уравнений (2) рассматривается в области 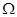, ограниченной поверхностью 
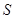, состоящей из трех достаточно гладких частей: 
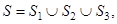где 
− поверхность поля; 
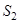− вертикальная боковая поверхность; 
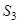− почва (не обязательно плоское).
Обозначим единичный вектор внешней нормали к поверхности как 
В начальный момент времени концентрации вредителей равны некоторым известным функциям:
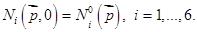(4)
Граничные условия на поверхности поля 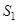. Вредители, независимо от направления перемещения (поверхность 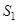), движутся по касательной к ней: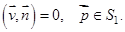 
Векторы скорости насекомых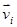 
имеют через эту поверхность ненулевой поток за счет осаждения. Поэтому на поверхности 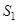граничное условие запишется следующим образом (диффузионный и конвективный потоки равны по модулю и противоположны по знаку):
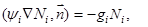
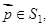
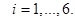(5)
Граничные условия на боковой границе 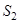. Цилиндрическая (боковая) граница 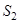области 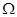вертикальна, поэтому на 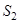выполняется следующее условие:
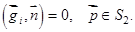(6)
Заметим, что из соотношений (3) — (5) следует, что:
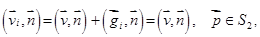(7)
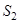представляет собой (далекую) границу с оставшейся частью поля. Обозначим часть поверхности 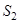, на которой 
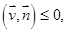как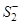 
, остальную часть, где 
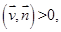как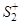 
. Смоделируем границу: 
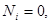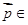
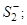
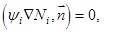если 
если .
Поток воздуха не проходит сквозь почву (поверхность ), поэтому движется по касательной к нему:
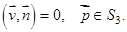(8)
Потребуем, чтобы основание поля находилось снизу от области :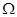
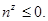(9)
Заметим, что из соотношений (3.5.9) — (3.5.10) следует, что на поверхности :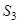 
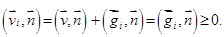(10)
Выражение (11) выполняется в силу микротурбулентного воздушного обмена, поэтому вредители не оседают на почву из-за турбулентной диффузии. Однако они оседают за счет гравитационного осаждения, поэтому граничные условия для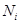 
на поверхности 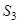будут выглядеть следующим образом:
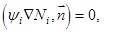
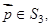
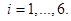(11)
Будем предполагать, что существует классическое решение задачи:
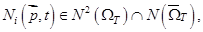где 
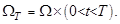(12)
Докажем единственность решения: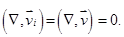 
Допустим, что существуют два различных решения: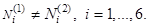 
Подставим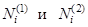 
в систему (1), а также в начальные и граничные условия, вычтем друг из друга:
(13)
Умножим каждое уравнение (14) на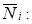 
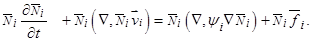(14)
Запишем формулу производной произведения для выражения 
с учетом
:
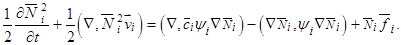(15)
Проинтегрируем равенство (17) с учетом граничных и начальных условий сначала по области 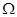, а затем по времени от 
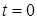до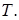 
Левая часть после интегрирования принимает вид:
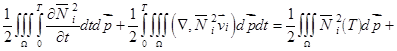
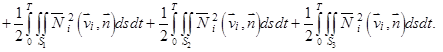(16)
Преобразуем интегралы по частям поверхности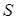 
:
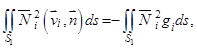
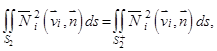
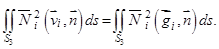
После ряда преобразований получаем:
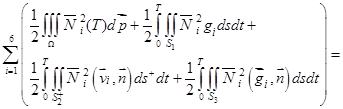
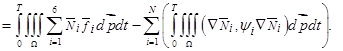(17)
Левая часть равенства (21) больше либо равна нулю, так как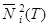 
− функция возводится в квадрат (концентрации 
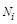необязательно положительны); 
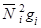− функция возведена в квадрат и умножена на положительную скорость осаждения примесей; 
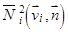− выражение неотрицательно, так как на поверхности 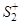, по которой берется интеграл, 
=
; 
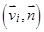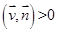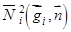− выражение неотрицательно, так как на поверхности 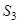, по которой берется интеграл, 
.
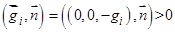В случае, если правая часть равенства (21) меньше либо равна нуля, т. е. выполняется:
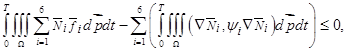(18)
обе части равенства (2) должны быть равны нулю и, значит, все слагаемые левой части тождественно равны нулю во всей рассматриваемой области для любого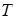 
. В частности, 
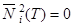, откуда следует совпадение двух решений и 
.
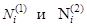Выясним, при каких условиях справедливо неравенство (19). Для этого оценим выражение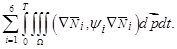 
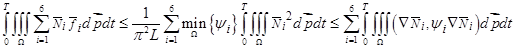и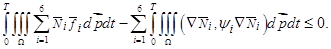 
Следовательно, если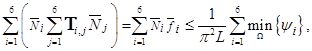 
то неравенство (2) справедливо.
Вывод: таким образом, условие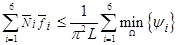 
является достаточным условием единственности решения задачи (1) — (3).
Литература:
1. Мозаичная структура распределенного сообщества трансгенной кукурузы. Кажарова И. А. Известия Южного федерального университета. Технические науки. 2009. Т. 97. № 8. С. 148–155.
2. Об одной демогенетической модели адаптации насекомых к изменению кормовой базы. Ляпунова И. А. Известия Южного федерального университета. Технические науки. 2013. № 4. С. 235–239.
3. Сухинов А. И., Чистяков А. Е. Параллельная реализация трехмерной модели гидродинамики мелководных водоемов на супервычислительной системе//Вычислительные методы и программирование: новые вычислительные технологии. 2012. Т. 13. № 1. С. 290–297.
