Введение
Хорошо известно, что интегральные операторы с ядрами Пуассона и Коши проектируют классы Гельдера на единичной окружности на соответствующие классы аналитических функций ([1], [2]) На этом основаны многие вопросы математической физики (теория краевых задач типа Привалова, Гильберта, Римана и т. д.) ([1], [2]) Однако во многих задачах комплексного и функционального анализа возникает потребность проектирования более широких классов функций, заданных на том или ином множестве на соответствующие пространства аналитических функций.
В последние годы появляется много работ российских и зарубежных математиков посвященных проектированию 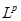 пространства суммируемых функций на весовые пространства Бергмана. Эти вопросы изложены в известных монографиях ([3], [4]) В этой статье мы продолжаем исследование по проблематике, изложенной в работе [5]. Впервые было замечено, что интегральные операторы с ядрами Бергмана проектируют классы измеримых в единичном круге функций, производная которых по углу суммируема, отображается на пространства аналитических функций удовлетворяющих такому же условию.
пространства суммируемых функций на весовые пространства Бергмана. Эти вопросы изложены в известных монографиях ([3], [4]) В этой статье мы продолжаем исследование по проблематике, изложенной в работе [5]. Впервые было замечено, что интегральные операторы с ядрами Бергмана проектируют классы измеримых в единичном круге функций, производная которых по углу суммируема, отображается на пространства аналитических функций удовлетворяющих такому же условию.
В этой статье мы докажем близкие теоремы в том случае, когда производная по одному направлению, скажем по радиусу, имеет определенный рост при приближении к единичной окружности (в случае полуплоскости — к вещественной оси)
Формулировка и доказательство основных результатов статьи
Для формулировки доказательства основных результатов введем следующие обозначения.
Пусть 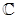 - комплексная плоскость,
- комплексная плоскость, 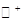 - верхняя полуплоскость, т. е.
- верхняя полуплоскость, т. е. 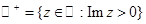 ,
, 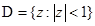 — единичный круг на комплексной плоскости
— единичный круг на комплексной плоскости 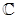 ,
, 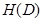 – множество всех аналитических функций в D. Пусть далее
– множество всех аналитических функций в D. Пусть далее 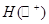 — множество аналитических функций в
— множество аналитических функций в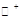 ,
,
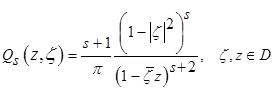 — ядро Бергмана для круга порядка
— ядро Бергмана для круга порядка 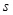 , а
, а
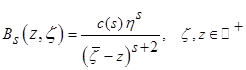 — ядро Бергмана для полуплоскости
— ядро Бергмана для полуплоскости 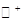 порядка
порядка 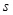 ,
,
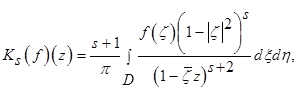 где
где 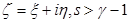 . (1)
. (1)
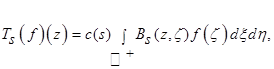 где
где 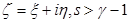
Если 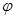 - монотонно возрастающая положительная функция на
- монотонно возрастающая положительная функция на 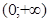 , а
, а 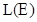 — множество измеримых функций на измеримом множестве E, то
— множество измеримых функций на измеримом множестве E, то
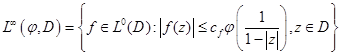
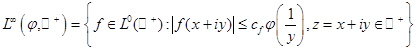 ,
,
где 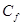 — некоторое положительное число, зависящее только от
— некоторое положительное число, зависящее только от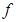 , φ — некоторая монотонно растущая положительная функция на
, φ — некоторая монотонно растущая положительная функция на 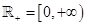 ,
, 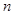 — неотрицательное целое число, то есть
— неотрицательное целое число, то есть 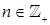
Как указывалось выше, такие операторы были исследованы в 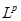 пространствах суммируемых функций ([3], [4]). Мы изучаем поведение этих операторов в следующих пространствах суммируемых функций:
пространствах суммируемых функций ([3], [4]). Мы изучаем поведение этих операторов в следующих пространствах суммируемых функций:
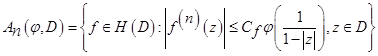 , (2)
, (2)
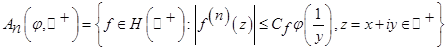
Определение. Скажем, что функция 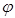 принадлежит классу
принадлежит классу 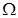 , если существует положительное число
, если существует положительное число 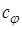 , такое что:
, такое что: 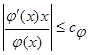 и
и 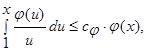
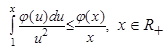 и φ удовлетворяет оценке
и φ удовлетворяет оценке 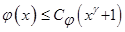 , при всех
, при всех 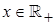 и при некотором
и при некотором 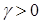 .
.
Основной результат статьи являются доказательство следующих двух утверждений.
Теорема 1.Пусть функция 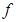 интегрируема в
интегрируема в 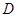 и такая, что
и такая, что 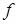 и
и 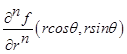 принадлежат классу
принадлежат классу 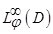 , при некотором
, при некотором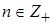 , где
, где 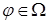 . Тогда
. Тогда 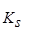 тоже принадлежит классу
тоже принадлежит классу 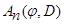 .
.
Теорема 2. Пусть 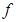 - интегрируема в
- интегрируема в 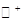 и такая, что
и такая, что 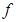 и
и 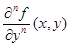 принадлежат классу
принадлежат классу 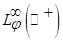 при котором
при котором 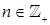 . Тогда функция
. Тогда функция 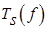 принадлежит классу
принадлежит классу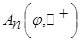 т. е. оператор
т. е. оператор 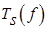 отображает пространство функций n-ая производная, которых принадлежит классу
отображает пространство функций n-ая производная, которых принадлежит классу 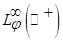 на пространство
на пространство 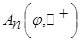 .
.
Доказательство теоремы 1
Пусть функция 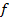 — удовлетворяет условию:
— удовлетворяет условию:
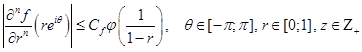
Докажем, что аналогичная оценка справедлива для функции 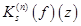 .
.
Указанную оценку мы получим при 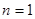 , при
, при 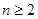 основные рассуждения сохраняются, появляются только технические сложности.
основные рассуждения сохраняются, появляются только технические сложности.
Итак, пусть 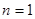 . Заметим, что указанный интеграл (1) абсолютно сходится, если
. Заметим, что указанный интеграл (1) абсолютно сходится, если 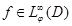 и
и 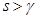 . Действительно, имеем
. Действительно, имеем
,
В последней оценке мы воспользовались тем, что 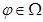 . Учитывая также оценку
. Учитывая также оценку
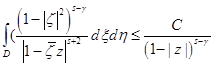
окончательно получим:
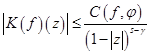 ,
,
где 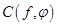 - постоянное число, зависящие только от
- постоянное число, зависящие только от 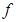 и
и 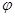 .
.
Перейдем к оценке функции 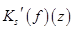 .
.
Вычисляя производную функции 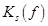 получаем:
получаем:
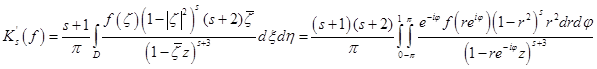 .
.
Преобразуем внутренний интеграл, интегрируя его по частям и учитывая, что 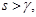 получим:
получим:
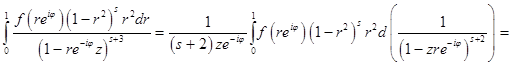

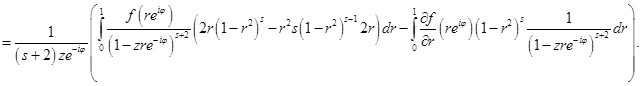
Тогда
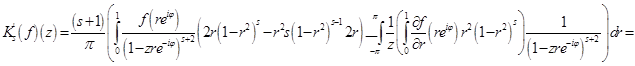
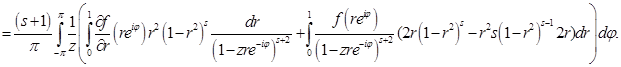
Введем следующие обозначения:
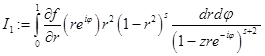
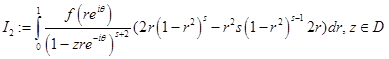
Следующая оценка 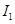 получается стандартным образом (см. [5])
получается стандартным образом (см. [5])
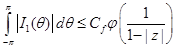
Перейдем к оценке 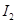 . Для этого сначала оценим
. Для этого сначала оценим 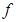 ,учитывая, что
,учитывая, что 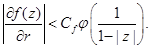
Имеем
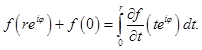
Отсюда получаем
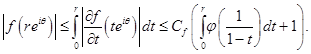
Сделаем замену переменной в последнем интеграле, 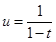 получим
получим
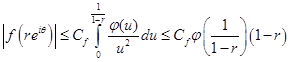 (3)
(3)
В последней оценке мы воспользуемся тем, что функция 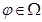 . Вернемся к оценке
. Вернемся к оценке 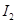 . Не ограничивая общность, можно предположить, что
. Не ограничивая общность, можно предположить, что 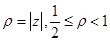 .
.
Тогда получим:
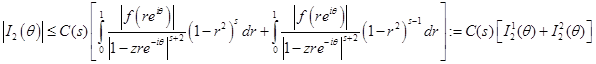 (4)
(4)
Интеграл 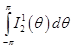 оценивается стандартным образом (см. [3], стр.106). Другими словами нетрудно установить, что
оценивается стандартным образом (см. [3], стр.106). Другими словами нетрудно установить, что
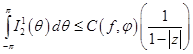 (5)
(5)
Для доказательства теоремы 1 остается получить соответствующую оценку для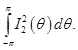
Учитывая оценку (3) имеем:
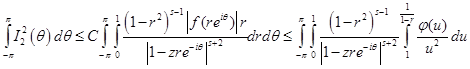 .
.
Следовательно,
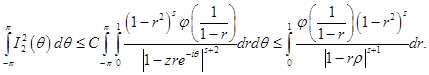
Применяя рассуждения, используемые при доказательстве результатов в работе [5] отсюда окончательно получаем:
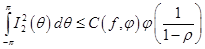 (6)
(6)
Объединяя оценку (4),(5), (6) получаем:
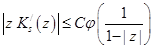 (7)
(7)
где 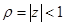
Но поскольку функция 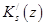 принадлежит классу
принадлежит классу 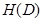 , то из оценки (7) немедленно следует утверждение теоремы.
, то из оценки (7) немедленно следует утверждение теоремы.
Теорема доказана.
Доказательство теоремы 2 проводится, аналогичным образом, учитывая свойства ядра Бергмана 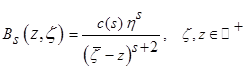 для полуплоскости.
для полуплоскости.
Замечание. Используя интегральное представление аналитической функции по свойствам ядра Бергмана через вещественную часть и классические теоремы Привалова и Харди — Литлвуда из теоремы 1 и теоремы 2 сразу следует, что, если гармоническая функция и в замкнутом круге имеет модуль непрерывности 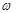 , то гармонические сопряженные функции будут иметь такой же модуль непрерывности в замкнутом круге, если ω удовлетворяет хорошо известному условию Бари — Стечкина (см. [6]).
, то гармонические сопряженные функции будут иметь такой же модуль непрерывности в замкнутом круге, если ω удовлетворяет хорошо известному условию Бари — Стечкина (см. [6]).
Литература:
1. Мусхелишвили Н. И. Сингулярные интегральные уравнения.Граничные задачи теории функций и некоторые их приложения к математической физике. М.-Л. Гостехиздат. 1946г. 448с.
2. Гахов Ф. Д. Краевые задачи. М.:Наука, 1977г.
3. Djrbashian M. M., Shamoyan F. A. Topics in theory of 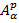 spaces, Teubner — Verlag, Leipzig, 1988.
spaces, Teubner — Verlag, Leipzig, 1988.
4. H. Hedermalm, B. Korenblum, K. Zhu. Theory of Bergman spaces, Springer — Verlag New York, 2000.
5. М. Н. Андрейчик, Е. В. Коптенок, А. А. Орлова Интегральные операторы с ядрами типа Бергмана в пространствах аналитических функций, с заданным модулем непрерывности // Молодой ученый. — 2013. — № 8 (55) — с.1–5.
6. Бари Н. К., Стечкин С. Б. Наилучшие приближения и дифференциальные свойства двух сопряженных функций // ТММО, Том 5, 1956.







