В статье рассмотрен способ оптимизации движения с учётом обеспечения локализации затора на линейном участке дороги. Приведены зависимости рабочей скорости перемещения машины от некоторых параметров и показателей.
Ключевые слова:комбинированная дорожная машина, дорожный затор, скоростной режим дороги.
С увеличением количества автомобилей на дорогах возник целый спектр проблем в области оптимизации дорожного движения, в том числе быстрый износ дорожного покрытия приводит к потребности частого ремонта. Ремонтируемый участок дороги недоступен для дорожного движения, что приводит к дополнительному усугублению ситуации. Также возникают проблемы, связанные с содержанием дорог при помощи комбинированных дорожных машин (КДМ). КДМ имеют скорости выполнения рабочих операций гораздо меньшие, чем нормальная скорость на дороге. В результате ситуация на дороге усугубляется — за машиной образуется автомобильная пробка.
Закономерности образования заторов рассматриваются в теории транспортных потоков. При этом отмечается, что позиции данной теории не позволяют достичь полного понимания природы автомобильных пробок [1]. С каждым годом количество знаний в этой области накапливается, однако в теории транспортных потоков (см. например [2], [3], [4]) рассматриваются положения, которые нельзя в полной мере применить к движению КДМ. А именно: 1) КДМ не является полноценным участником дорожного движения, поскольку с её помощью достигается цель содержания дорог, а не перемещения; 2) КДМ является препятствием на дороге, параметры которого необходимо оптимизировать.
В таких условиях целесообразно разработать специализированные математические модели. Основным показателем режима движения КДМ является её скорость Vкдм, именно её величина должна оптимизироваться. Для определения способа оптимизации режима движения КДМ необходимо рассмотреть, в каких условиях дорожная ситуация терпит качественные изменения. Если затор, образовавшийся за КДМ, локализован на участке дороги, не имеющем перекрёстков, то проблемы с движением имеют место собственно на загруженном участке дороги. Если затор достигает перекрестка, то проблемы возникают и на пересекающей дороге, в результате он имеет сетевое распространение. Такая ситуация имеет характерный качественный переход. В момент, когда «хвост» пробки достигает перекрёстка, можно переместить КДМ с дороги, в результате чего движение будет нормализовано.
Например, КДМ находится на обочине (или в кармане) и до ближайшего перекрёстка за КДМ есть некоторая дистанция L1 (см. рис. 1), следующий карман для съезда находится на некотором расстоянии L2 перед КДМ. Нужно подобрать такую скорость Vкдм движения КДМ, чтобы, пока она едет по дороге до следующего кармана, пробка не превысила бы длину L1+L2.
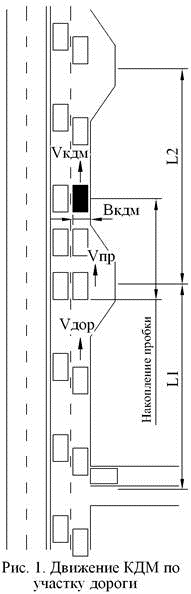
Водители автомобилей вынуждены объезжать (обгонять) перемещающуюся КДМ. От того, какая доля от полосы Вкдм занята, скорость объезда Vоб может меняться. Скорость движения КДМ и относительная скорость Vоб объезда КДМ формируют скорость затора или пробки Vп.
Дорога имеет скоростной режим Vдор, который в совокупности со скоростью пробки Vпр формирует скорость накопления пробки V нак.пр. Скорость накопления пробки определяет время Tпред.нак. предельного накопления (или допустимое время движения КДМ по дороге), в течение которого пробка займет дистанцию L1+L2. Именно за это время КДМ должна успеть преодолеть дистанцию L2, отсюда можно определить минимально возможную скорость движения КДМ Vкдм. Перечисленные факторы реализованы в математической модели оптимизации скоростного режима комбинированной дорожной машины (КДМ) при выполнении работ по содержанию. Исходная информация к расчёту с использованием модели находится в табл. 1. Перечень результатов расчёта содержится в табл. 2.
Наибольшая интенсивность использования КДМ приходится на зимний период, поэтому вопрос оптимизации имеет особенную важность именно для этого времени. Зимой при помощи КДМ выполняются работы по уборке снега и предупреждению образования льда. Перечисленные работы осуществляются преимущественно с использованием оборудования: “отвал”, “цилиндрическая подметальная щётка”, “распределитель реагента”. В математической модели предусмотрена оптимизация скоростного режима для условий, определяемых нахождением на КДМ перечисленного рабочего оборудования. Однако для обеспечения формулировки задачи в общей форме не исключена возможность дальнейшего развития модели путём незначительной доработки.
Таблица 1
Исходные данные
|
№ |
Наименование пункта исходной информации |
Обозначение |
Ед. измерения |
Числ. значение |
|
1 |
Ширина КДМ в долях от ширины полосы |
Вкдм |
доли |
1,0 |
|
2 |
Расстояние от места выезда на дорогу КДМ до перекрёстка за КДМ |
L1 |
км |
0,3 |
|
3 |
Расстояние от места выезда на дорогу КДМ до места съезда |
L2 |
км |
0,5 |
|
4 |
Скоростной режим дороги |
Vдор |
км/час |
90 |
Для анализа поведения математической модели произведём однофакторное варьирование пунктов исходной информации (см. табл. 1) с последующим построением графиков зависимости результатов расчёта.
Таблица 2
Результаты расчёта
|
№ |
Наименование пункта результата расчёта |
Обозначение |
Ед. измерения |
|
1 |
Допустимое время движения КДМ по дороге |
Тпред.нак |
часы |
|
2 |
Скорость накопления пробки |
Vнак.пр |
км/час |
|
3 |
Скорость пробки |
Vпр |
км/час |
|
4 |
Минимально возможная рабочая скорость перемещения КДМ |
Vкдм |
км/час |
|
5 |
Относительная (приведённая) скорость объезда КДМ |
Vоб |
км/час |
Рассмотрим следующий расчётный случай. КДМ находится в кармане (или на обочине) участка магистрали, на расстоянии L1 за ней находится ближайший перекрёсток, на расстоянии L2 перед ней находится ближайший карман для съезда. Дорога имеет по две полосы движения в каждую сторону. КДМ выполняет работы по содержанию только на правой полосе. Во время нахождения на полосе дороги КДМ занимает часть от ширины полосы Вкдм.
Рассмотрим изменение дорожной ситуации (т. е. величины Vнак.пр, Vпр и других показателей — см. табл. 2) в период движения КДМ от одного кармана до другого при переменных условиях — произведём однофакторное варьирование пунктов 1–4 исходной информации.
Результаты варьирования ширины Вкдм представлены на рис. 2. При увеличении Вкдм падает относительная скорость объезда Vоб. Это приводит к падению скорости пробки (скорости потока в пробке) Vпр и, как следствие, возрастанию скорости накопления (удлинения) пробки Vнак.пр. Для того чтобы обеспечить возможность достижения КДМ следующего кармана до того, как «хвост» пробки достигнет перекрёстка за КДМ, необходимо увеличить скорость перемещения КДМ Vкдм. Увеличение скорости Vкдм приводит к снижению времени его нахождения на дороге Тпред.нак.
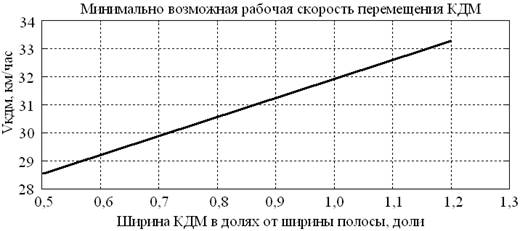
Рис. 2. Зависимость скорости Vкдм от ширины Вкдм
Результаты варьирования расстояния от места выезда на дорогу КДМ до перекрестка за КДМ L1 представлены на рис. 3. При увеличении L1 возрастает предельная длина пробки L1+L2. Поэтому можно допустить снижение скорости движения Vкдм и повышение времени пребывания КДМ на дороге Тпред.нак. Снижение Vкдм приводит к снижению скорости пробки Vпр и, как следствие, повышению скорости накопления пробки Vнак.пр.
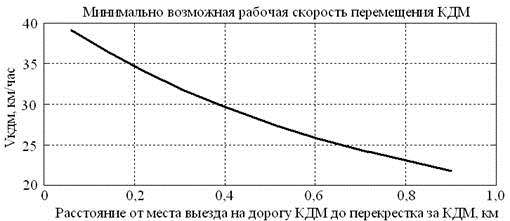
Рис. 3. Зависимость скорости Vкдм от расстояния L1
Результаты варьирования расстояния от места выезда на дорогу КДМ до места съезда L2 представлены на рис. 4. При увеличении L2 возрастает предельная длина пробки L1+L2, однако КДМ должна успевать освобождать участок длиной L2 с такой скоростью Vкдм, чтобы «хвост» пробки не успел достигнуть ближайшего перекрестка до момента съезда с дороги. В результате с увеличением L2 необходимо повысить скорость пробки Vпр и, как следствие, снизить скорость накопления пробки Vнак.пр. Указанное достигается путём повышения скорости Vкдм и снижения времени пребывания КДМ на дороге Тпред.нак.
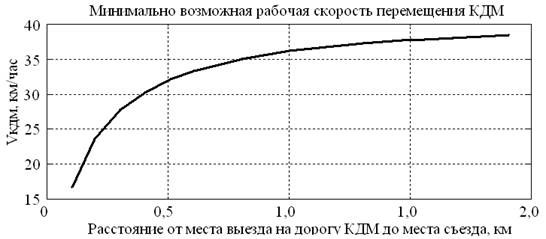
Рис. 4. Зависимость скорости Vкдм от расстояния L2
Результаты варьирования нормальной скорости движения (скоростной режим дороги) Vдор представлены на рис. 5. В результате увеличения Vдор возрастает скорость накопления пробки Vнак.пр, поэтому нужно увеличить скорость пробки Vпр, что достигается путём повышения скорости движения Vкдм. Повышение Vкдм приводит к снижению продолжительности пребывания её на дороге Тпред.нак.
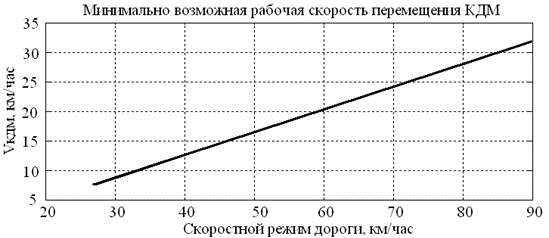
Рис. 5. Зависимость скорости Vкдм от скорости Vдор
Заключение
Таким образом, получены зависимости основного показателя режима движения КДМ, подлежащего оптимизации — скорости Vкдм. Из рассмотрения которых можно заключить, что математическое моделирование представляет собой гибкий инструмент анализа дорожной ситуации в целом и оптимизации режима движения КДМ в частности, который в последствии можно алгоритмизировать и внедрить в состав аппаратных средств автоматизированного регулирования.
Каждый участок дороги имеет свои особенности — частота расположения перекрестков или карманов для съезда, ширина и количество полос движения, скоростной режим, интенсивность движения, от которой зависит скорость накопления пробки и др.. В целом всё это определяет потребность многократного расчёта при помощи математической модели. От расчёта к расчёту исходная информация переменна, необходимо следить за правильным её составлением. Также необходимо следить за правильной систематизацией результатов расчёта и их применением. При этом можно управлять скоростным режимом одной КДМ, которая последовательно находится на анализируемых участках дороги, либо несколькими КДМ, которые одновременно работают в нескольких местах.
Учитывая сказанное, можно предположить, что с использованием обозначенной выше математической модели могут быть разработаны достаточно сложные и многофункциональные алгоритмы управления и мониторинга с использованием автоматизированных средств наблюдения.
Литература:
1. Studying the ebb and ow of stop-and-go; Los Alamos Lab using cold war tools to scrutinize tra‑c patterns alan sipress washington post stawriter, Thursday, August 5, 1999, www.science.com
2. Швецов В. И. Математическое моделирование транспортных потоков // Автоматика и телематика. — 2003. — № 11.
3. Хейт Ф. Математическая теория транспортных потоков / М.:Мир, 1966. — 286 с.
4. Смирнов Н. Н., Киселёв А. Б., Никитин В. Ф., Юмашев М. В. Математическое моделирование автотранспортных потоков // мех-мат МГУ, 1999.







