Синтез структуры мультисервисной сети на базе генетических алгоритмов

В статье рассмотрены вопросы структурного синтеза мультисервисной сети с помощью генетических алгоритмов. При этом все возможных решений представлены в виде хромосомы, а структура сети в виде графов. Такой подход позволяет объединить в единый комплекс решение задачи автоматизации процесса принятия проектных решений в проектирования структуры распределенных мультисервисных сетей. Предложены алгоритмы формирования структуры сети на базе модифицированных операторов кроссоверинга и мутации хромосомы.

The paper deals with the structural synthesis of multi-service network using genetic algorithms. Thus all possible solutions presented in the chromosome, and the network structure in the form of graphs. This approach allows us to combine into a single complex automation solution process of making design decisions in designing the structure of distributed multi-service networks. The algorithms for the formation of the network structure on the basis of modified and mutation operator’s krossoveringa hromosomy.V article questions the structural synthesis of multi-service network using genetic algorithms. Thus all possible solutions presented in the chromosome, and the network structure in the form of graphs. This approach allows us to combine into a single complex automation solution process of making design decisions in designing the structure of distributed multi-service networks. The algorithms for the formation of the network structure on the basis of the modified operators krossoveringa and chromosome mutation.

Для решения задачи структурного синтеза мультисервисной сети в первую очередь, необходимо определить пространство потенциальных решений.

Пространством потенциальных решений 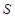в нашем случае является множество всех возможных структур проектируемой сети представленных в виде графа.

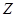Пространство представлений 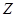, соответствующее всем возможным структурам сети из пространства 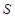, представим в виде:

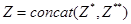,                                                                                                     (1)

где 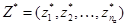- множество дуг, представляющие информацию о взаимосвязи между абонентами и коммутационными узлами сети;

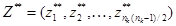- множество дуг, носящие в себе информацию о взаимосвязях только между коммутационными узлами сети [1–2].

Элементы вектора 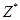, строго упорядочены в соответствии с номерами абонентов сети 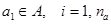. Каждый 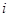- ый элемент вектора 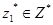содержит номер коммутационного узла 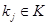, к которому подключен 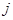-ый абонент сети :

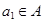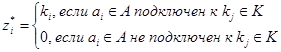                                                                 (2)

Элементы вектор 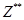является конкатенацией строк матрицы смежности 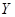, лежащих выше главной, диагонали:

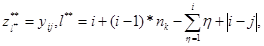                                                                     (3)

где, .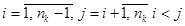

Очевидно, что длина дуг при таком кодировании равна

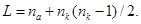                                                                                                    (4)

В результате применении операций над графами могут образовываться петля или тупиковые состояния, т. е. решения, не удовлетворяющие параметрическими и структурным условиям сети 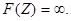 Для решения поставленной задачи будем использовать генетические алгоритмы [3–4]. При этом пространство потенциальных решений представляется в виде хромосомы.

При этом 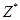будем называть FP(FirstPartofChromosome) и 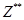будем называть SP(SecondPartofChromosome)- частями хромосомы. Тогда для устранения возможных случаев образования петель предлагаются применения модифицированных оператор кроссоверинга и мутации.

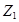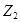 Модифицированный оператор кроссоверинга. Пусть имеются две родительские структуры и , представленные графам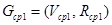и и 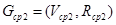. На базе этих графов необходимо получить граф  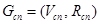соответствующий структуре потомка 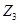, образующегося в результате применения оператора кроссоверинга.

Для этого, на графе 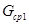и 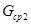выделим подграфы

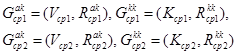                                                                            (5)

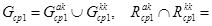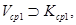
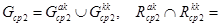где Ø,

Ø,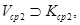

Сформулируем множества каналов связей, несовпадающих у 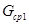и :

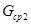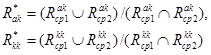                                                                                  (6)

Введем следующие обозначения:

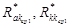- соответственно подмножества ребер типа <абонент. узел> → <комм. узел> и <комм. узел> → <комм. узел>, принадлежащие только родительской структуре 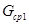, т. е. 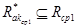и ;

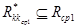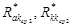- соответственно подмножества ребер типа <абонент. узел> → <комм. узел> и <комм. узел> → <комм. узел>, принадлежащие только родительской структуре 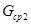, т. е. 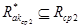и 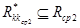, тогда <абонент. узел> → <комм. узел> и <комм. узел> → <комм. узел>, принадлежащие только родительской структуре 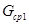, т. е. 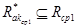и ;

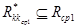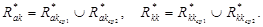                                                                     (7)

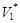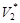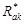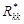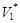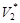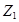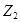Определяем множество вершин и инцидентных ребрам из множества и . Место расположения элементов вершин из множества  и , соответственно в векторах и , определяет точки кроссоверинга.

Формируем множество весовых коэффициентов ребер 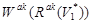типа <абонент. узел> → <комм. узел>, инцидентных абонентскому узлу (АУ) из множества  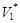и множества весовых коэффициентов ребер 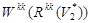типа <комм. узел> → <комм. узел>, инцидентных коммутационному узлу (КУ) из множества 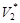, такой что:

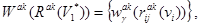                                                                                     (8)

где 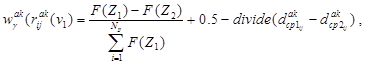 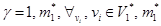- мощность множества 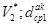- длина канала связи (ребра) 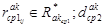- длина КС (ребра) 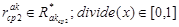- приведенные (нормированные) значения длины КС.

Весовые коэффициенты 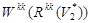 вычисляются по формуле

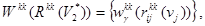                                                                                    (9)

где 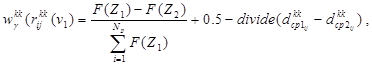 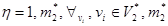- соответственно мощность множеств 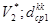- длина канала связи (ребра) 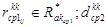- длина КС (ребра) 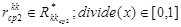- приведение (нормированное) значения длины каналов связи.

Формирование структуры потомка 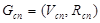осуществляется по этапном решением задач формирования FP и SP –частей хромосомы потомка.

1.      Формируем FP — части хромосомы в виде подграфа:

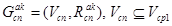 и 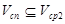.                                                                      (10)

Поскольку в структуре потомка должны присутствовать все узлы сети, то множество вершин графа потомка 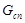будет равно множеству вершин графа, представляющего любой родительской структурой, т. е. .

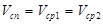Определяем подмножества ребер 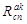графа 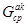, соединяющих абонентские узлы сети с его коммутационным узлом:

а) пусть 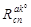- пустое множество ребер типа <абонент. узел> → <комм. узел>. К множеству 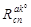добавляем подмножество ребер, совпадающих у родительских структур 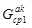и ,

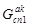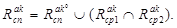                                                                                           (11)

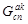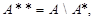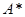После выполнения данной операции в подграфе остаются неподключенными к коммутационным узлам те абонентские узлы, которые принадлежат подмножеству где - подмножество абонентских узлов сети, инцидентных ребрам из множества .

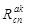б) случайным образом выбираем число 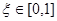и формируем подмножество ребер 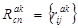, инцидентным к АУ .

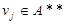с) объединяем подмножества ребер 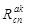и .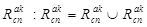

В результате получаем подграф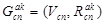, отображающий структуру FP — части хромосомы потомка, представляющий информацию о соединении абонентских узлов сети с соответствующими коммутационными узлами (рис. 1).

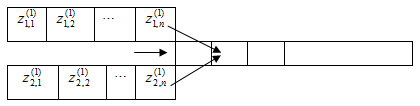
Рис 1. Схема соединения абонентского узла с коммутационным узлом сети.

2.      Формируем SP- части хромосомы потомка в виде подграфа

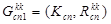,                                                                                                          (12)

где 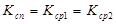и .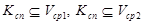

Исходя из 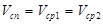, получим 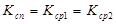. Учитывая это, решение второй подзадача можно свести к определению подмножества ребер.

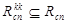а) пусть 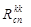- пустое множество ребер типа <комм. узел> → <комм. узел>. Определяем подмножество ребер, совпадающих у родительских структур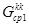и :

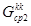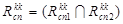                                                                                                        (13)

Подмножестве коммутационных узлов 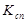разделим на две непересекающиеся подмножества 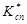и :

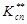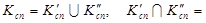Ø, 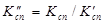,                                                   (14)

где 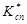- подмножества коммутационных узлов сети, инцидентных ребрам из множества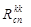, 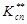- подмножество взвешенных коммутационных узлов.

б) случайно выбирая коммутационный узел 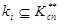, находим ребро  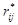подмножества ребер 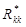, соединяющее его с любом другим коммутационным узлом 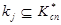по критерию минимума затрат, т. е. 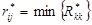. Найденное ребро добавим в подмножестве 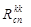, и коммутационный узел  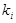переводим из подмножества 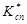и:

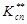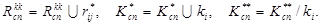                                                       (15)

Поиск ребра 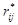 из подмножества ребер  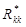осуществляется до тех пор, пока подмножество взвешенных вершин не будет пустым, т. е. 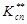=Ø.

с) объединяем подмножества ребер 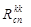и:

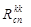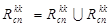                                                                                                           (16)

д) в случае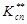=Ø в графе 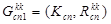образуются изолированным подграфы. Эти подграфы последовательно объединяем с помощью случайно выбранного ребра  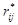из множества всех возможных ребер.

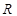После выполнения данных операций имеемSP- часть хромосом потомка, представляющую информацию о соединении коммутационных узлов между собой в виде подграфа.

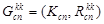                                                                                                             (17)

Учитывая (8), граф 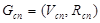, представляющий структуру хромосомы потомка, можем определить как:

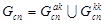                                                                                                             (18)

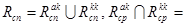где Ø, .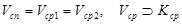

Таким образом, мы получаем граф 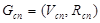отображающий структуру потомка 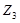, образующегося в результате применения оператора кроссоверинга.

Модифицированный оператор мутации. Пусть имеется родительская структура 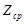, представленная графом 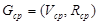. В результате применения оператора мутации получим граф 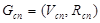, соответствующий структуре потомка 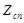, образующегося из графа 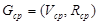. Для решения этой задачи на начальном этапе предположим, что:

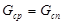                                                                                                                       (19)

Принимая во внимание (9), на графе 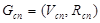 определяем подграфы:

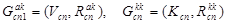,                                                                             (20)

такие, что

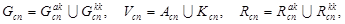
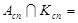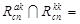Ø, Ø, .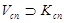

Из множества ребер 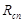 выбираем случайное ребро 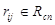и удаляем его

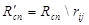.                                                                                                                (21)

Если данное ребро относится к классу ребер типа <абонент. узел> → <комм. узел>, т. е. 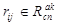, абонентский узел 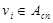, остающийся отключенным от сети, будем подключать к коммутационному узлу согласно следующему правилу:

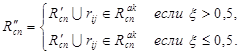                                                                           (22)

где 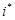- номер абонентского узла сети 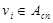остающийся в результате выполнения операции (16); 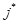- номер коммутационного узла сети 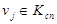определенная по критерии минимум затрат 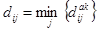, 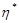-случайное натуральное число, соответствующее номеру коммутационного узла сети 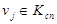, 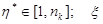- случайное число, находящееся в интервале [0,1],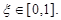

Таким же образом будут внесены изменения в FP- части хромосомы 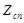. Если удаленного ребро относится к классу ребер типа <комм. узел> → <комм. узел>, т. е. 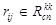, тогда в результате выполнения операции (21) в графе 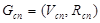образуются изолированные подграфы:

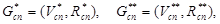                                                                                (23)

такие что,

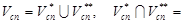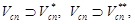
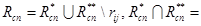Ø,

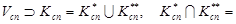Ø,

Ø

В таком случае изолированные подграфы соединяются следующим образом:

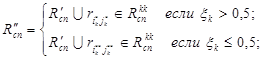                                                                     (24)

где 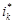, 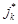- соответственно, номера коммутационных узлов сет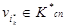и и 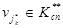 определенные по критерию минимума затрат 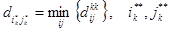- соответственно, случайные натуральные числа, соответствующие номерам коммутационных узлов сет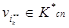и и 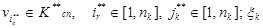- случайное число находящееся в интервале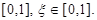

В результате выполнения данной процедуры будет внесена изменения в SP- частью хромосомы .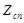

Таким образом, принимая 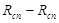, получим граф 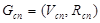, представляющий структуру новой хромосомы потомка.

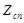Рассмотренные предпосылки позволяют сделать вывод о том, что необходимо комплексное решение задач проектирования мультисервисной сети, в том числе и задач топологического проектирования на базе генетических алгоритмов. Анализ методик синтеза топологий мультисервисной сети показывает, что в качестве базовых проектирование структуры сети могут быть использованы методы определения структур: древовидной конфигурации произвольной формы, древовидной иерархической сети, а также кратчайшей связывающей сети заданной конфигурации. Сложности, которые могут возникнуть при использовании этих методик, состоят в необходимости объединения этих методик в единый комплекс, позволяющий автоматизировать процесс принятия проектного решения распределенных мультисервисных сетей.

Литература:

1. Райншке К., Ушаков И. A. Оценка надежности систем с использованием графов. — М.: Радио и связь, 1988. — 208 с.

2. Свами М., Тхуласираман К. Графқ, сети, алгоритмы. М.: Мир, 1984.

3. Круглов В. В., Дли М. И., Голунов Р. Ю. Нечеткая логика и искусственные нейронные сети. М.: Физматлит, 2001.

4. Усков А. А., Кузьмин А. В. Интеллектуальные технологии управления. Искусственные нейронные сети и нечеткая логика. — М.: Горячая Линия — Телеком, 2004.