В настоящее время потребность в деревянных строительных конструкциях возрастает ежегодно. Значит, выбор наиболее оптимальных и экономически выгодных конструктивных схем является наиболее перспективных областей исследований в области деревянных конструкций [1]. Авторами уже были опубликованы работы в данном направлении [2], [3].
Цель данного исследования определить оптимальные способы закрепления рам. Оптимальность оценивается путем сравнения материалоемкости различных вариантов. В качестве вариантов были оценены три типа рам: трех шарнирная; одна шарнирная, жесткая. Данные рамы показаны на рис. 1–3.
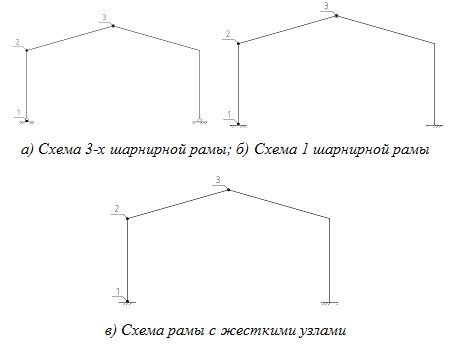
Рис. 1.
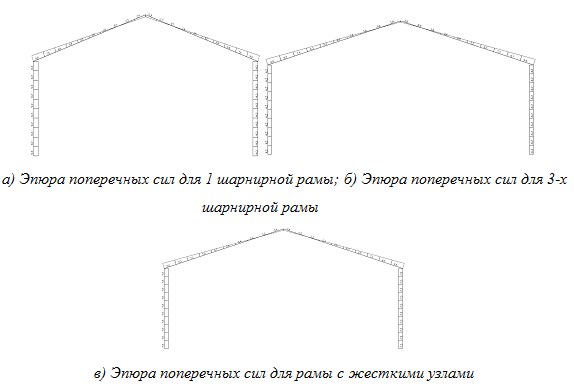
Рис. 2.
|
Qz |
1 шарнирная |
3-х шарнирная |
бесшарнирная |
|
Точка 1 |
9,2 |
6,2 |
7,5 |
|
Точка 2 |
9,2 |
6,2 |
7,5 |
|
Точка 3 |
2,9 |
2,0 |
2,4 |
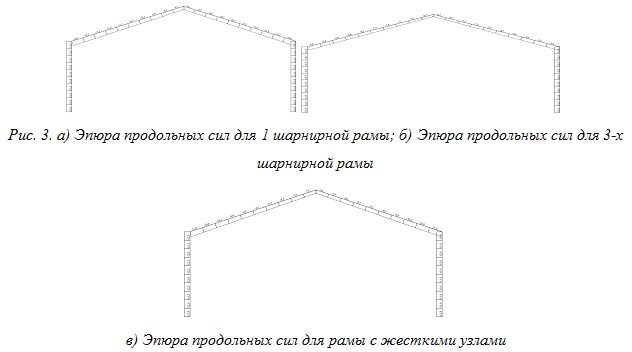
Рис. 3.
|
Nz |
1 шарнирная |
3-х шарнирная |
бесшарнирная |
|
Точка 1 |
12,5 |
12,5 |
12,5 |
|
Точка 2 |
12,5 |
12,5 |
12,5 |
|
Точка 3 |
9,1 |
6,3 |
7,5 |
Анализируя эпюры M, N, Q приходим к выводу, что продольная сила в трех рамах практически одинакова, а моменты и поперечные силы различны. Так если рассматривать жесткую и одношарнирную раму, то видно что моменты в карнизном узле одинаковы, а на опоре различны. Но помимо усилий M, N, Q важную роль играет распределение напряжений по высоте сечения. Для анализа и решения проблемы были определены и посчитаны 3 рамы.
Конструктивный расчет рамы
1. Расчет одно шарнирной рамы.
Расчетные усилия M=26,26т·м=262,6кН×м и N=-8,78т=87,8кН.
При h=1200мм определяем b.
Принимаем b=150мм.
Проверка прочности.
Размеры сечения b×h=150×1200мм (0,15×1,2м). Находим значения коэффициентов к расчетному сопротивлению mб =0,8 и mсл =0,99. Расчетное сопротивление для сосны с учетом этих коэффициентов:
![]()
Длина полурамы (она же является и расчетной длиной):
![]()
Гибкость рамы:
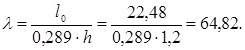
Коэффициент продольного изгиба:
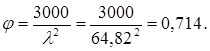
Площадь брутто сечения: F=b×h=15,0×120,0=1800см2.
Учет переменности высоты сечения по длине стойки производим путем введения коэффициента kЖN, значение которого определяем по СНиП II-25–80 прил.4, табл.1:
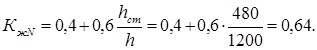
Определяем значение коэффициента:
![]()
Расчетный момент сопротивления проверяемого сечения:
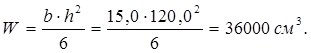
Проверка прочности сечения производим по формуле:
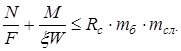
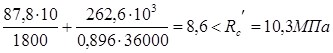
Прочность сечения обеспечена.
2. Расчет трех шарнирной рамы.
Расчетные усилия M=34,4т·м=344кН×м и N=-8,68т=86,8кН.
При h=1200мм определяем b.
Принимаем b=175мм.
Проверка прочности.
Расчетные усилия M=34,4т·м=344кН×м и N=-8,68т=86,8кН. Размеры сечения b×h=175×1200мм (0,175×1,2м). Находим значения коэффициентов к расчетному сопротивлению mб =0,8 и mсл =0,99.
Расчетное сопротивление для сосны с учетом этих коэффициентов:
![]()
Длина полурамы (она же является и расчетной длиной):
![]()
Гибкость рамы:
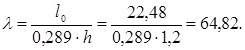
Коэффициент продольного изгиба:
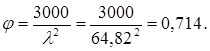
Площадь брутто сечения: F=b×h=17,5×120,0=2100см2.
Учет переменности высоты сечения по длине стойки производим путем введения коэффициента kЖN, значение которого определяем по СНиП II-25–80 прил.4, табл.1:
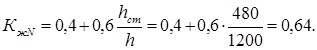
Определяем значение коэффициента:
![]()
Расчетный момент сопротивления проверяемого сечения:
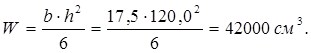
Проверка прочности сечения производим по формуле:
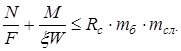
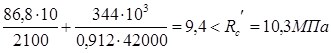
Прочность сечения обеспечена.
3. Расчет жесткой рамы
Расчетные усилия M=22,74т·м=227,4кН×м и N=-8,67т=86,7кН.
При h=1200мм определяем b.
Принимаем b=120мм.
Проверка прочности.
Расчетные усилия M=22,74т·м=227,4кН×м и N=-8,67т=86,7кН. Размеры сечения b×h=135×1200мм (0,135×1,2м). Находим значения коэффициентов к расчетному сопротивлению mб =0,8 и mсл =0,99.
Расчетное сопротивление для сосны с учетом этих коэффициентов:
![]()
Длина полурамы (она же является и расчетной длиной)
![]()
Гибкость рамы:
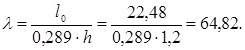
Коэффициент продольного изгиба:
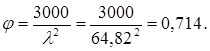
Площадь брутто сечения: F=b×h=13,5×120,0=1620см2.
Учет переменности высоты сечения по длине стойки производим путем введения коэффициента kЖN, значение которого определяем по СНиП II-25–80 прил.4, табл.1:
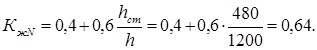
Определяем значение коэффициента:
![]()
Расчетный момент сопротивления проверяемого сечения:
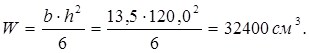
Проверка прочности сечения производим по формуле:
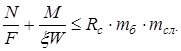
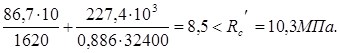
Прочность сечения обеспечена.
Таким образом, можно составить диаграмму материалоёмкости (рис.4), из которой видно, что наиболее материалоемкая рама имеет трёхшарнирное опирание. Выбрав оптимальный вариант конструкций деревянных рам, можно существенно снизить экономические издержки при строительстве зданий и сооружений
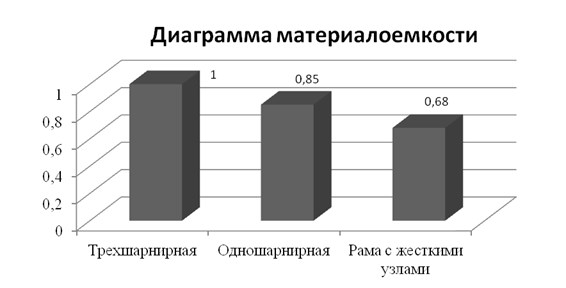
Рис.4. Диаграмма материалоёмкости
Литература:
1. Арискин М. В. Исследование напряженно-деформированного состояния гнутых карнизных узлов рам [Текст] / М. В. Арискин, Д. В. Гуляев, И. Ю. Агеева // Молодой ученый. — 2013. — № 3. — С. 19–25.
2. Арискин М. В Теоретические исследования напряженно-деформированного состояния элементов соединений на вклеенных шайбах [Текст] / Арискин М. В., Д. В. Гуляев, И. Ю. Агеева, Гарькин И. Н.// Молодой ученый. — 2013. — № 2. — С. 27–31.
3. Арискин М. В Современные тенденции развития проектирования в строительстве [Текст] / Арискин М. В., Д. В. Гуляев, И. Ю. Агеева, Гарькин И.Н // Молодой ученый. — 2012. — № 10. — С. 31–33.







