В статье изложен способ повышения эффективности управления транспортными и пешеходными потоками на регулируемом перекрестке. Реализованы валидация, проектирование и верификация. Разработан программный комплекс моделирования регулируемого перекрестка.
Результаты математического моделирования и формализация модели на ПЭВМ, позволяют повысить эффективность работы светофора на регулируемом перекрестке.
Ключевые слова: Имитационное моделирование, валидация, проектирование, верификация, качество модели, чувствительность, адекватность, устойчивость, программный комплекс, диаграмма классов, логическая модель базы данных.
Повышение эффективности управления транспортными и пешеходными потоками на регулируемых перекрестках является актуальной задачей. С каждым годом машин на дорогах городов становится больше. Решение проблемы пробок невозможно без комплексного и многофакторного изучения. Одной из причин появления дорожных заторов является неэффективное управление потоками на регулируемых перекрестках. И предложения по улучшению дорожной ситуации, перед их реализацией, должны быть смоделированы на компьютере при помощи соответствующих методов. В качестве такого метода используется метод Монте-Карло.
Имитационное моделирование — метод исследования и оценки эффективности систем, поведение которых зависит от случайных факторов. В основе имитационного моделирования лежит статистический эксперимент (метод Монте-Карло), реализация которого невозможна без применения средств вычислительной техники [1].
Постановка задачи. Разработать имитационную модель, позволяющую моделировать транспортные и пешеходные потоки на регулируемом перекрестке и формализовать ее на ЭВМ.
Данная система должна отвечать следующим требованиям:
- иметь возможность моделирования транспортных и пешеходных потоков, на регулируемом перекрестке;
- иметь возможность определения наилучшего режима работы светофора;
- иметь возможность сохранения результатов моделирования;
- иметь возможность вывода результатов статистического эксперимента;
- иметь возможность обработки результатов статистического эксперимента.
Перекресток дорог (улиц) со всеми его геометрическими параметрами, транспортными и пешеходными потоками при их взаимодействии представляет сложную систему. Рассмотрим ее основные характеристики:
- проезжая часть имеет полосы движения, k=1,2,…, т;
- одни транспортные и пешеходные потоки j=1,2,…,n прибывшие к стоп-линии с интенсивностью λ, образуют очереди при запрещающих движение тактов (сигналов) светофора. Другие транспортные средства /ТС/, прибывшие к стоп-линии при разрешающих движение тактах светофора, проезжают перекресток без остановки перед ним;
- пешеходы и ТС, находящиеся в очереди, при включении разрешающего сигнала начинают движение;
- при проезде перекрестка ТС могут изменить направление движения — прямо, налево, направо. Если из текущей полосы совершение маневра невозможно, происходит попытка смены полосы движения;
- пешеходы и ТС, застигнутые сменой разрешающего такта на запрещающий в зоне перекрестка или вне ее у стоп-линии, успевают пересечь перекресток с выполнением необходимых маневров при промежуточном (желтом) такте;
- предполагается, что по каждому направлению к границе перекрестка –стоп-линии прибывают транспортные потоки. При этом случайные моменты времени появления распределяются по экспоненциальному закону. Появление происходит на определенном расстоянии от перекрестка. Движение транспортных средств осуществляется в соответствии с моделью движения.
Выбор направления движения на перекрестке осуществляется в соответствии с вероятностями указанными пользователем.
Разработан программный комплекс с использованием программного обеспечения: Microsoft Visual C# и СУБД MySQL.
Впрограмме применяется микроскопическая модель движения автомобилей. За основу взята модель умного водителя (The Intelligent Driver Model, IDM), разработанная Мартином Трайбером, Ансгаром Хенеком и Дирком Хельбингом [2].
Уравнение движения имеет вид:
![]() ,
,
где a — максимальное ускорение;
![]() — текущая скорость;
— текущая скорость;
![]() - максимальная разрешенная скорость;
- максимальная разрешенная скорость;
![]() - минимальное расстояние между автомобилями;
- минимальное расстояние между автомобилями;
![]() — расстояние до впередиидущего автомобиля;
— расстояние до впередиидущего автомобиля;![]()
![]() — скорость приближения;
— скорость приближения;
b — ускорение торможения.
Автомобиль плавно набирает скорость от 0 до желаемой ![]() с ускорением, которое зависит от скорости
с ускорением, которое зависит от скорости ![]() в данный момент времени и от заданного максимального ускорения a. Снижение скорости в случае возникновения препятствия перед автомобилем осуществляется с помощью функции которая зависит от расстояния до препятствия
в данный момент времени и от заданного максимального ускорения a. Снижение скорости в случае возникновения препятствия перед автомобилем осуществляется с помощью функции которая зависит от расстояния до препятствия ![]() , скорости автомобиля
, скорости автомобиля ![]() , от параметров
, от параметров ![]() . Стохастичность моделирования достигается за счет того, что параметры, характеризующие индивидуальные особенности стиля вождения водителя, вычисляются отдельно для каждого автомобиля случайным образом в соответствии с равномерным распределением с разбросом 20 %. В качестве исходных значений принимаются
. Стохастичность моделирования достигается за счет того, что параметры, характеризующие индивидуальные особенности стиля вождения водителя, вычисляются отдельно для каждого автомобиля случайным образом в соответствии с равномерным распределением с разбросом 20 %. В качестве исходных значений принимаются ![]() =1,5м, α = 2 м/
=1,5м, α = 2 м/![]() , b = 2 м/
, b = 2 м/![]() .
.
Калибровка и численные эксперименты с этой моделью показали, что ее свойства устойчивы к вариации параметров; модель демонстрирует реалистическое поведение при разгоне и торможении и воспроизводит основные наблюдаемые свойства транспортного потока.
Для определения наилучшего режима работы светофора используется генетический алгоритм. Генетический алгоритм оперирует конечным множеством решений (популяцией) — генерирует новые решения как различные комбинации частей решений популяции, используя такие операторы, как отбор, рекомбинация (кроссовер) и мутация [3].
Последовательность действий:
1) генерация начального набора светофоров, в которых параметры сгенерированы случайным образом в виде двоичного кода, под каждый параметр отводится 8 бит;
2) вычисление среднего времени ожидания для каждого из светофоров (с использованием модели);
3) выбор параметров светофора, при которых время ожидания является наименьшим;
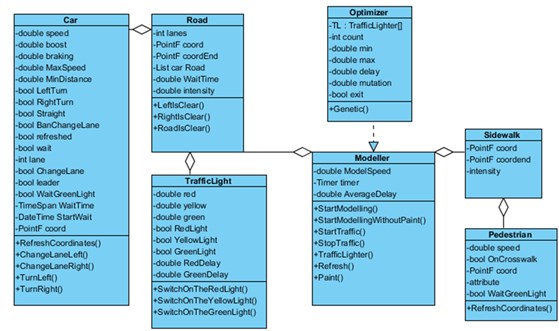
Рис. 1. Диаграмма классов
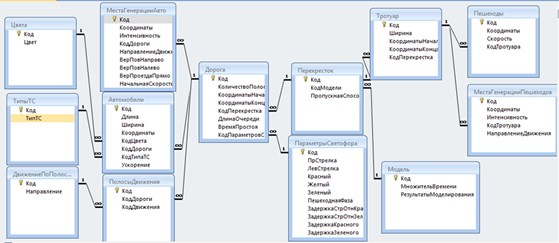
Рис. 2. Логическая модель базы данных
4) определение пар для кроссовера. Выбор пар происходит случайным образом;
5) кроссовер;
6) мутация особей с заданной вероятностью;
7) редукция (сокращение набора до начального значения);
8) если наименьшее время ожидания не менялось в течении заданного количества циклов, происходит выбор светофора с наименьшим временем ожидания и остановка алгоритма.
Проведена проверка качества модели. Определены оценки адекватности, устойчивости и чувствительности модели.
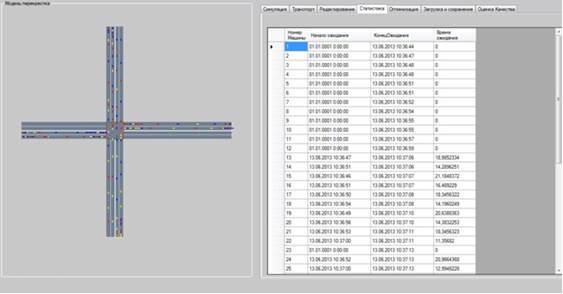
Рис. 3. Результат работы программы
Диаграмма классов приведена на рис. 1. Логическая модель базы данных приведена на рис. 2. На рис. 3 приведены результаты статистического эксперимента на ПЭВМ.
Результаты проведенных исследований позволили сделать выводы.
1. Разработана программа моделирования регулируемого перекрестка.
2. Разработанная программа позволяет повысить эффективность управления транспортными и пешеходными потоками на регулируемом перекрестке.
3. Результаты работы могут быть использованы для дальнейшего исследования.
Литература:
1. Гультяев А. К. MATLAB 5.3. Имитационное моделирование в среде Windows: практическое пособие. — СПб: КОРОНА принт, 2001. — 400 с.
2. Гасников А. В. Введение в математическое моделирование транспортных потоков. — Москва, 2010. — 360 с.
3. Гладков Л. А. Генетические алгоритмы/Гладков Л. А., Курейчик В. В., Курейчик В. М. — Ростов-на-Дону, 2004. — 400 с.







