Введение
В данной статье выполняется разработка математической модели канала связи с белым Гауссовым шумом соответствующей заданным критериям. Предложенная математическая модель апробируется в задачах моделирования каналов связи с использованием не кодированных многопозиционных цифровой фазовой манипуляции и когерентной цифровой частотной манипуляции. В заключение приводятся результаты проверки адекватности разработанной математической модели.
Постановка задачи
Разработать математическую модель канала связи с белым Гауссовым шумом, соответствующую следующим критериям:
1) математическая модель должна быть адекватной;
2) математическая модель должна быть реализуемой;
3) математическая модель должна позволять выполнять моделирование процесса передачи данных в целом;
4) математическая модель должна позволять выполнять моделирование процессов происходящих в передатчике и, при необходимости, давать возможность влиять на них;
5) математическая модель должна позволять выполнять моделирование процессов происходящих непосредственно в среде передачи данных и, при необходимости, давать возможность влиять на них;
6) математическая модель должна позволять выполнять моделирование процессов происходящих в приемнике и, при необходимости, давать возможность влиять на них;
7) математическая модель должна быть расширяемой.
Исходя из последнего из вышеперечисленных требований, разрабатываемая математическая модель должна быть применима в широком кругу задач. Однако, исходя из 4-го и 5-го пунктов вышеперечисленных требований очевидно, что математическая модель такого рода не может быть абсолютно универсальной. Другими словами, не существует такого аналитического выражения, которым могла бы быть описана желаемая математическая модель так, чтобы она была применима для любой задачи без каких-либо доработок и/или адаптаций.
В связи с этим, в рамках данной работы, мы ограничимся разработкой математической модели для следующих частных случаев:
1) передатчик (способ модуляции):
a. многопозиционный цифровой фазовый манипулятор (модулятор);
b. когерентный многопозиционный цифровой частотный манипулятор (модулятор);
2) приемник (демодулятор):
a. корреляционный универсальный (т. е. такой корреляционный приемник, который может принять любой сигнал при условии, что ему известна вся информация об ансамбле сообщений используемых передатчиком).
Многопозиционная цифровая фазовая манипуляция и когерентная многопозиционная цифровая частотная манипуляция выбраны по той причине, что являются фундаментальными хорошо изученными способами модуляции которые используются и по сей день.
Корреляционный приемник выбран в связи с тем, что среди существующего на сегодняшний день разнообразия приемников, применяемых в тех или иных областях, корреляционный приемник является наиболее совершенным и лежит в основе оптимальных приемников для современных высокоскоростных телекоммуникационных систем [1].
Разработка математической модели
В качестве основы для разрабатываемой математической модели возьмем стандартное векторное представление канала связи: 
, где 
— принятый сигнал в момент времени 
, 
— переданный сигнал в момент времени , а 
— значение белого Гауссового шума в момент времени .
При этом, стоит отметить, т. к. моделируется непосредственно реальный физический процесс, все значения являются действительными числами.
Основной идеей предлагаемой математической модели является нормализация энергии передаваемого сигнала к единице. Это приведет к тому, что в независимости от характера используемых способов модуляции, белый Гауссовый шум будет налагаться на все переданные сигналы равномерно. Это актуально для таких способов модуляции как, например, цифровая квадратурная амплитудная манипуляция и цифровая амплитудно-фазовая манипуляция (также известная как цифровая асинхронная фазовая манипуляция), при использовании которых, потенциально, возможна ситуация, когда разные сигналы (сигналы представляющие разные символы алфавита) имеют разною мощность и, соответственно, энергию, что, в свою очередь, может привести к тому, что при моделировании белый шум может быть наложен неправильно.
Спектральную плотность мощности белого Гауссового шума описывается следующим выражением: 
, где 
— постоянная Планка (в
), 
— постоянная Больцмана (в 
), 
— температура окружающей среды (в Кельвинах), 
— частота (в Гц), а 
— искомая спектральная плотность мощности для заданной при температуре . Таким образом, при комнатной температуре 
, белый Гауссовый шум сохраняет до 90 % от своего максимума вплоть до частоты 
(2 терагерца). Учитывая то, что для используемых на сегодняшний день телекоммуникационных систем эта частота недостижима, при моделировании существующих каналов связи можно принять что какой бы ни была частота дискретизации, использованная для моделирования, влияние белого шума будет сохраняться. При моделировании теоретических телекоммуникационных систем, которые могут работать в терагерцовом диапазоне и выше стоит учитывать приведенную выше формулу спектральной плотности мощности для определения степени влияния белого Гауссового шума на передаваемые сигналы [2].
Величина белого Гауссового шума, влияющая на передаваемы сигнал в момент времени описывается следующим аналитическим выражением: 
, где 
— функция нормального распределения для заданных математического ожидания и дисперсии, а 
— дисперсия шума.
В свою очередь, дисперсия белого Гауссового шума определяется следующим выражением: 
, где 
— спектральная плотность мощности шума.
Энергия одного символа алфавита модулятора равна 
, где 
— количество бит приходящееся на одно сообщение модулятора, 
— кодовая частота (например, для не кодированных каналов равна 1, а для кодированных каналов добавляющих 50 % избыточных данных — 0.5), а 
— энергия, приходящаяся на 1 переданный бит.
Исходя из описанного выше принципа нормализации энергии передаваемого сигнала, можно записать следующе выражение связывающее дисперсию белого шума отношение сигнал-шум для одного бита информации: 
. Отсюда легко можно выразить дисперсию белого шума: 
.
Для соответствия описанному выше представлению канала связи, передаваемые сигналы должны быть нормализованы до единичной энергии. Иными словами, 
, где 
— исходный сигнал, а 
— энергия исходного 
-того сигнала.
Для когерентной цифровой многопозиционной частотной манипуляции описанное выше выражение имеет следующий вид: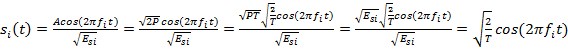 
исходя из того, что мощность сигнала равна 
. Следует отметить, что полученное выражение является выражением для -той базисной функции для данного способа модуляции.
Для цифровой многопозиционной фазовой манипуляции описанное выше выражение имеет следующий вид: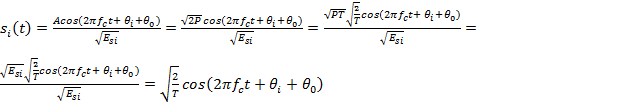 
исходя из того, что мощность сигнала равна . При необходимости, из полученного выражения можно получить базисные функции для данного типа модуляции путем несложных тригонометрических преобразований: 
. Отсюда ортонормальные базисные функции цифровой многопозиционной фазовой манипуляции: 
и 
.
Оптимальный корреляционный приемник, распознающий принятые сигналы по принципу максимального правдоподобия, должен иметь полную информацию о выходном ансамбле сообщений передатчика и может быть описан следующим аналитическим выражением: 
, где 
— принятый сигнал, 
— эталонный сигнал из ансамбля передатчика отвечающий символу входного алфавита , — длительность символа, а — принятый символ.
Проверка адекватности математической модели
Разработанная математическая модель была реализована с помощью компьютерного языка программирования Python. С использование данной реализации было выполнено моделирование цифровой многопозиционной фазовой манипуляции и когерентной цифровой многопозиционной частотной манипуляции.
Примеры временных диаграммы процессов, происходящих в передатчике, линии связи и приемнике приведены на рисунках 1 и 2.
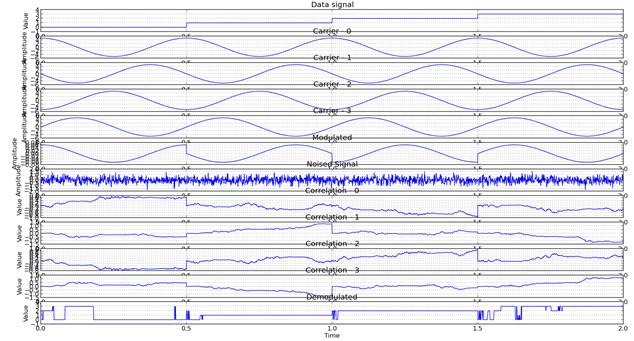Рис. 1. Пример временных диаграмм для канала связи с белым Гауссовым шумом с использованием цифровой четырехпозиционной фазовой манипуляции
Также были построены зависимости вероятностей символьный ошибки, которые приведены на рисунках 3 и 4. Наряду с экспериментальными данными на данных рисунках отложены теоретические данные.
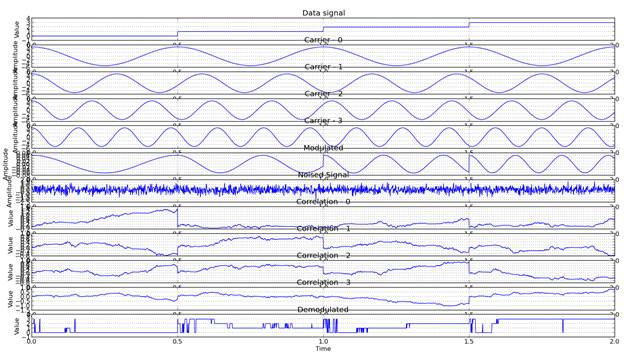Рис. 2. Пример временной диаграммы для канала связи с белым Гауссовым шумом с использованием когерентной цифровой четырехпозиционной частотной манипуляции
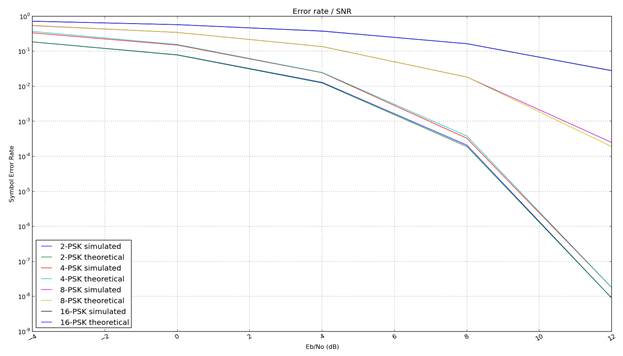Рис. 3. Вероятность символьной ошибки в зависимости от отношения 
для канала связи с белым Гауссовым шумом с использованием цифровой многопозиционной фазовой манипуляции
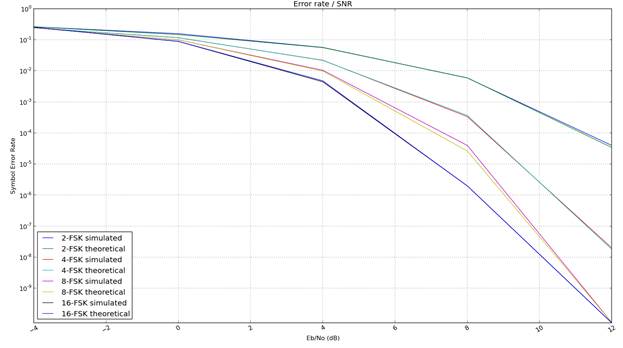Рис. 4. Вероятность символьной ошибки в зависимости от отношения для канала связи с белым Гауссовым шумом с использованием когерентной цифровой многопозиционной частотной манипуляции
Исходя из полученных результатов можно сделать вывод о том, что разработанная математическая модель является адекватной и пригодной для использования в научных исследованиях, т. к. полученные вероятности ошибки совпадают с теоретическими.
Выводы
На основании требований, являющихся исходными данными, была выполнена разработка математической модели для каналов данных с белым Гауссовым шумом.
Предложенная математическая модель была апробирована в задачах моделирования четырехпозиционной цифровой фазовой манипуляции и когерентной четырехпозиционной цифровой частотной манипуляции.
На основании полученных экспериментальных данных было принято решение об адекватности разработанной математической модели и её пригодности для использования в научных исследованиях.
Литература:
1. Digitl Communications. Fundamentals and Applications. Second Edition. B. Sklar. 2003.
2. Digitl Communication. J. G. Proakis. Masoud Salehi. 2007
