В данной статье предлагается модернизировать существующие аппараты гибридных сетей Петри и вложенных сетей Петри с целью получения формализма сетей Петри, направленного на исследование технологических процессов произвольной структуры. Новый аппарат получается путем частичного объединения и расширения формализмов сетей Петри.
В общем случае вложенную гибридную сеть Петри можно определить следующим образом:
NHPN = {Atom, Lab, SN(HPN), (ENl,..., ENk), ?},
рассмотрим составляющие этого множества.
1) Atom = Var ? Con — множество атомов, состоящее из множеств Var = {v,...} имен переменных (позиций) и Con = Conatom ? Connet{c,...} имен констант или фишек (состоящее, в свою очередь, из множеств Conatom атомарных и Connet сетевых констант). Константы из Connet интерпретируются как маркированные обыкновенные сети Петри (сетевые фишки). А константы из Conatom — как индивидуальные фишки, не имеющие собственной структуры (атомарные фишки).
2) Lab = Labv ? Labh — множество меток. Где Labv = {l1,l2,...} и Labh = {λ1, λ 2,...} — два непересекающихся множества меток. Элементы множества Labv используются для вертикальной синхронизации переходов, а элементы Labh — для горизонтальной синхронизации.
3) SN(HPN) — системная сеть в составе вложенной гибридной сети Петри (ВГСП), представляющая собой гибридную сеть Петри (ГСП): HPN = (Р, Т, Pre, Post, D, С).
Р = Pd ? Рс — множество позиций сети, объединяющее множества дискретных позиций Pd и непрерывных позиций Рс. Непрерывные позиции содержат только метки, отражающие уровень сигнала в текущий момент времени в данной позиции. Дискретные позиции могут содержать одновременно метки двух типов: обыкновенные (атомарные) и сетевые, представленные маркированными обыкновенными сетями Петри.
Т = Тd ? Тc ? Тk ? ТE — множество переходов, объединяющее множества дискретных Td и непрерывных Тс переходов, расширенное за счет множеств переходов квантования Тk и экстраполяции ТE. Для каждого типа переходов определены характеризующие их параметры: временные интервалы задержек срабатывания, пропускная способность, периоды квантования и экстраполяции.
Pre, Post — матрицы инцидентности, характеризующие множество дуг, они определяются аналогично матрицам инцидентности ГСП с соблюдением всех необходимых правил и замечаний к ним. В системной части ВГСП, как и в ГСП, не должно существовать дуг, соединяющих непрерывную позицию с дискретным переходом. При этом если существует дуга, соединяющая дискретную позицию с непрерывным переходом, то должна существовать и обратная дуга, образующая в данном месте графа петлю.
Все возможные варианты соединений вершин графа ВГСП приведены ниже на рисунке 1.
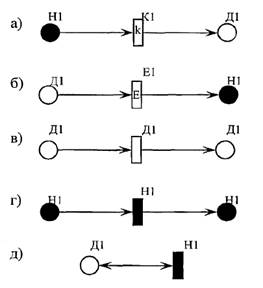
Рис. 1. Возможные варианты соединения вершин графа ВГСП
Отметим, что для переходов квантования и экстраполяции входными могут быть также обыкновенные дуги, соединяющие их с дискретными и непрерывными позициями, соответственно, но они не переносят метки через переход и выполняют роль условий срабатывания для перехода.
D: Тt → R+ — функция, определяющая интервалы задержки для дискретных временных переходов как некоторый постоянный порог срабатывания.
С: Тс → ![]() x
x ![]() - функция, определяющая пропускную способность для непрерывных переходов (
- функция, определяющая пропускную способность для непрерывных переходов (![]() = R+ ? {∞}).
= R+ ? {∞}).
Маркировка сети назначает для каждой дискретной позиции целое число фишек с учетом их потенциала, а для каждой непрерывной позиции — присутствует в ней сигнал или нет.
4) (ENl,...,ENk)(k ≥ l) — конечный набор обыкновенных сетей Петри. Сети ENl,...,ENk представляют собой элементные сети в составе вложенной гибридной сети Петри NHPN.
5) ? — функция пометки переходов, помечающая некоторые переходы системной сети метками из Labv и некоторые переходы в элементарных сетях метками из Labv ? Labh.
Отметим, что графически NHPN представляется в виде графа, вершинами которого являются множества позиций Р = Pd ? Рс и переходов Т = Тd ? Тc ? Тk ? ТE сети. На графе множество дискретных позиций Pd изображается кружками, множество непрерывных позиций Рс — закрашенными кружками, множество дискетных временных переходов TD изображаются прямоугольниками, множество непрерывных переходов ТC — закрашенными прямоугольниками, множества переходов квантования ТK и экстраполяции ТЕ — прямоугольниками, помеченными буквами К и Е, соответственно.
Введем в предлагаемый аппарат характерное для сетей Петри высокого уровня понятие веса дуг (v), что расширит описательные возможности предлагаемого аппарата.

Рис. 2. Вес дуги
Вес дуги может быть приписан как для входящих в переход дуг, так и для исходящих. При этом, вес входящей в переход дуги, может быть только положительным, он показывает, при какой минимальной маркировке входной позиции данный переход сработает. В этом случае из позиции удаляется число фишек равное весу исходящей из позиции дуги. Положительный вес исходящей из перехода дуги показывает, во сколько раз увеличится число проходящих через переход фишек, при добавлении их в выходные позиции перехода. По умолчанию вес дуги равен 1.
Существенным добавлением в аппарат является возможность использования дробных и отрицательных значений для веса исходящей из перехода дуги.
Дробный вес дуги v позволяет сравнивать маркировку входной для перехода позиции с заранее заданным значением. Допустим, нам необходимо определить момент, когда в позиции Д1 (Д — дискретные) появится 10 фишек (рисунок 2.), тогда определим вес дуги как 0,05. В случае когда маркировка Д1 меньше 10, в позицию Д2 «будет добавляться» 0 фишек, при m(Д1)=10 в позицию Д2 добавится одна фишка (исходя из правил округления десятичных дробей).
При построении различных вычислительных систем (в том числе и при реализации типовых динамических звеньев) требуется находить разность двух величин, в обыкновенных сетях Петри есть возможность находить только сумму двух величин. Отрицательный вес дуги позволяет сформировать отрицательную маркировку в той или иной позиции, при сложении которой с заданной положительной маркировкой другой позиции, получается искомая разность величин.
Кроме того, в аппарат внесено следующее условие: если вес исходящей из перехода дуги меньше 0, то из входящих в переход позиций удаляется и добавляется со знаком минус в выходную позицию все количество фишек, находящихся в ней в данный момент времени. Причем у перехода может быть только одна исходящая дуга с отрицательной величиной веса.
При использовании отрицательного веса дуги следует говорить о модифицированной маркировке, определяющей не количество фишек в позиции, а числовую величину, сформированную в данной позиции сети. Либо о потенциале фишек находящихся в этой позиции, маркировка при этом будет по-прежнему отражать количество фишек в данной позиции. Независимо от трактовки маркировки сети, в этом случае уравнения динамики сети не изменятся.
Кроме введения в аппарат понятия веса дуги предлагается дополнить его понятием ингибиторных дуг. Такая дуга запрещает срабатывание перехода при маркированной ее входной позиции. Использование ингибиторных дуг позволяет существенно расширить описательные возможности аппарата.
Определим в поведении ВГСП следующие четыре типа шагов срабатывания:
1. Системно-автономный шаг — это срабатывание перехода системной сети в соответствии с правилами для ГСП, при этом элементные сети рассматриваются как фишки, не имеющие собственной структуры. Такой шаг может переместить, породить или убрать объекты, но не может изменить их внутреннее состояние.
2. Элементарно-автономный шаг меняет только внутреннее состояние (маркировку) элементной сети, не меняя ее местонахождения в системной сети. Этот шаг выполняется в соответствии с обычными правилами срабатывания для переходов сетей Петри.
3. Шаг горизонтальной синхронизации есть одновременное срабатывание двух переходов в двух элементных сетях, находящихся в одной позиции системной сети (эти переходы должны быть помечены специальными метками горизонтальной синхронизации).
4. Шаг вертикальной синхронизации используется для синхронизации перехода в системной сети с некоторыми переходами элементных сетей. Вертикальная синхронизация означает одновременное срабатывание перехода системной сети и переходов (помеченных дополнительной меткой) элементных сетей, задействованных в этом срабатывании.
Предлагаемый модифицированный аппарат позволяет проводить одновременный анализ непрерывной и дискретной составляющих гибридных систем. С его помощью можно проводить наблюдение за исследуемой системой в целом, а не за отдельными ее частями. Возможность представления отдельных частей системы в виде ВСП позволяет упростить восприятие большой и громоздкой СП, сделать модель системы более наглядной и понятной для рядового исследователя. Кроме того, с помощью модифицированного аппарата ВСП возможно исследование элементов обслуживания в гибридных системах. Применение механизмов синхронизации между переходами расширяют возможности представления все более усложняющихся и растущих технических систем. Введение понятий веса дуги, расширяющих и запрещающих дуг, делает предлагаемый формализм более выразительным и мощным средством описания различных дискретно-непрерывных систем. Введение в аппарат новых переходов позволяет ввести в сети Петри такое понятие теории управления как обратные связи, а значит, расширяет возможности построения на базе предлагаемого формализма моделей технологических процессов.
Литература:
1. Бусленко Н. П. Моделирование сложных систем. — М.: Наука, 1978. — 400с.
2. Давыдов Д. В. Методы и модели анализа сетей АСУ с поддержкой качества обслуживания. — Вологда: ВоГТУ, 2007. — 139 с.
3. Куо Б. Теория и проектирование цифровых систем управления, перевод с английского. — М.: Машиностроение, 1986. — 446с.
4. Питерсон Дж. Теория сетей Петри и моделирование систем. — М.: Мир, 1984.-264с.







