Использование преобразования Гильберта-Хуанга для формирования моделей фонем русского языка в задаче распознавания речи

В статье исследуются возможности использования преобразования Гильберта-Хуанга для создания моделей фонем русского языка в системе преобразования речи в текст. Производится сравнение предложенного метода с преобразованием Фурье и вейвлет-преобразованием. Расчеты показали, что метод Гильберта-Хуанга, несмотря на возможность выявления нелинейных изменений в сигнале, в первоначальном виде малопригоден для формирования признаков речевого сигнала (по крайней мере, в рамках нейросетевого подхода).

Ключевые слова: нейросеть, внутренние моды, распознавание фонем, вейвлет-преобразование.

Введение

Конечной целью создания систем распознавания речи является способность машины распознавать слова в акустическом сигнале с эффективностью, не меньшей по сравнению с аналогичной способностью человека. В ходе истории разработок наблюдался значительный прогресс: размер словаря вырос до нескольких миллионов слов, а сами системы эволюционировали от дикторозависимых к дикторонезависимым. Тем не менее, главные проблемы на сегодняшний день не решены. Это связано с вариабельностью речи из-за искажения речевого сигнала фоновым шумом, явлением коартикуляции, а также зависимости речевых характеристик от голоса и интонации.

Традиционные методы анализа данных предназначены, как правило, для линейных и стационарных сигналов и систем, и только в последние десятилетия начали активно развиваться методы анализа нелинейных, но стационарных и детерминированных систем, и линейных, но нестационарных данных (вейвлетный анализ, распределение Вигнера-Вилля и др.). Между тем, большинство естественных материальных процессов, реальных физических систем и соответствующих им данных в той или иной мере являются нелинейными и нестационарными. При анализе используются определенные упрощения, особенно в отношении априорно устанавливаемого базиса преобразования данных в новые, удобные для обработки и анализа метрические пространства. В связи с этим актуальность разработки новых устойчивых и универсальных методов формирования речевых признаков очевидна.

При создании системы преобразования речи в текст одна из самых важных задач — выбор единицы распознавания.Рассмотрим основные подходы, используемые в системах распознавания речи для формирования речевых признаков — моделей фонем. Наиболее распространенные методы анализа — это преобразование Фурье и вейвлет-анализ.

Оконное преобразование Фурье

Классическое преобразование Фурье имеет дело со спектром сигнала, взятым во всем диапазоне существования переменной. Нередко интерес представляет только локальное распределение частот, в то время как требуется сохранить изначальную переменную (обычно время).

С позиций точного представления произвольных сигналов и функций, преобразование Фурье имеет ряд недостатков, которые привели к появлению оконного преобразования Фурье и стимулировали развитие вейвлет-преобразования. Отметим основные из них [2]:

-          ограниченная информативность анализа нестационарных сигналов и практически полное отсутствие возможностей анализа их особенностей (сингулярностей), т. к. в частотной области происходит «размазывание» особенностей сигналов (разрывов, ступенек, пиков и т. п.) по всему частотному диапазону спектра.

-          появление эффекта Гиббса на скачках функций, при усечениях сигналов и при вырезке отрезков сигналов для локального детального анализа;

-          гармонический характер базисных функций, определенных в интервале от  до .

Неспособность преобразования Фурье осуществлять временную локализацию сингулярностей сигналов может быть частично устранена введением в преобразование так называемой движущейся оконной функции, имеющей компактный носитель. Использование оконной функции позволяет представлять результат преобразования в виде функции двух переменных — частоты и временного положения окна.

Оконное преобразование Фурье имеет следующий вид [2]:

,                                                                                      (1)

Вейвлет-преобразование и его применение в практике обработки сигналов

Вейвлет-преобразование стремительно завоевывает популярность в столь разных областях, как телекоммуникации, компьютерная графика, биология, астрофизика и медицина. Благодаря хорошей приспособленности к анализу нестационарных сигналов оно стало мощной альтернативой преобразованию Фурье в ряде медицинских приложений.

Главным элементом в вейвлет анализе является функция-вейвлет. Вообще говоря, вейвлетом является любая функция, отвечающая двум условиям:

1.      Среднее значение (интеграл по всей прямой) равен 0.

2.      Функция быстро убывает при .

Обычно, функция-вейвлет обозначается буквой .

В общем случае вейвлет преобразование функции выглядит так [4; 5]:

,                                     (2)

где  — ось времени,  — момент времени,  — параметр, обратный частоте, a (*) — означает комплексно-сопряженное.

Коэффициенты вейвлет-преобразования содержат комбинированную информацию об анализирующем вейвлете и анализируемом сигнале (как и коэффициенты преобразования Фурье, которые содержат информацию о сигнале и о синусоидальной волне). Выбор анализирующего вейвлета, как правило, определяется тем, какую информацию необходимо извлечь из сигнала. Каждый вейвлет имеет характерные особенности во временном и в частотном пространстве, поэтому иногда с помощью разных вейвлетов можно полнее выявить и подчеркнуть те или иные свойства анализируемого сигнала.

Многомасштабный вейвлет-анализосновывается на разложении сигнала по функциям, образующим ортонормированный базис [1; 3]. Любую функцию можно разложить на некотором заданном уровне разрешения (масштабе)  в ряд вида:

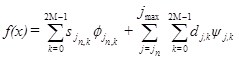,                                                                          (3)

где  и — масштабированные и смещенные версии скейлинг-функции (масштабной функции)  и «материнского вейвлета» ;

- коэффициенты аппроксимации;

- детализирующие коэффициенты.

Масштабирование и смещение функций и находится следующим образом:

,                                                                                                   (4)

,                                                                                                  (5)

В свою очередь сами функции и определяются так:

,                                                                                             (6)

,                                                                                            (7)

где

.                                                                                                         (8)

Дискретное вейвлет-преобразование не только раскладывает сигнал на некоторое подобие частотных полос (путем анализа его в различных масштабах), но и представляет временную область, т. е. моменты возникновения тех или иных частот в сигнале. Вместе, эти свойства характеризуют быстрое вейвлет-преобразование — альтернативу обычному быстрому преобразованию Фурье.

Таким образом, вейвлет-преобразование, в отличие от оконного преобразования Фурье, которое имеет постоянный масштаб в любой момент времени для всех частот, имеет лучшее представление времени и худшее представление частоты на низких частотах сигнала, на высоких частотах сигнала — лучшее представление частоты с худшим представлением времени. Введение вейвлет-преобразования дает возможность уменьшить влияние принципа неопределенности Гейзенберга на полученном частотно-временном представлении сигнала. С его помощью низкие частоты имеют более детальное представление относительно времени, а высокие — относительно частоты.

Преобразование Гильберта-Хуанга

Под преобразованием Гильберта-Хуанга (Hilbert-Huang transform — HHT) понимается метод эмпирической модовой декомпозиции (EMD) нелинейных и нестационарных процессов и Гильбертов спектральный анализ (HSA) [14]. Этот метод потенциально жизнеспособен для нелинейного и нестационарного анализа данных, специально для частотно-энергетических временных представлений.

EMD-HSA был предложен Норденом Хуангом в 1995 в США (NASA) для изучения поверхностных волн тайфунов, с обобщением на анализ произвольных временных рядов коллективом соавторов в 1998 г. [12; 14]. В последующие годы, по мере расширения применения алгоритма для других отраслей науки и техники, вместо термина EMD-HSA был принят более короткий термин преобразования HHT.

EMD (Empirical Mode Decomposition) — метод разложения сигналов на функции, которые получили название внутренних или «эмпирических мод». Метод представляет собой адаптивную итерационную вычислительную процедуру разложения исходных данных (непрерывных или дискретных сигналов) на эмпирические моды или внутренние колебания.

Огибающие сигналов. У каждого сигнала имеются локальные экстремумы: чередующиеся локальные максимумы и локальные минимумы с произвольным расположением по координатам (независимым переменным) сигналов. По этим экстремумам с использованием методов аппроксимации можно построить две огибающие сигналов: нижнюю — построенную по точкам локальных минимумов, и верхнюю — построенную по точкам локальных максимумов, а также функцию «среднего значения огибающих», которой отвечает срединная линия, расположенная в точности между нижней и верхней огибающими.

Функции внутренних мод сигналов. Модовая декомпозиция сигналов основана на предположении, что любые данные состоят из различных внутренних колебаний (intrinsic mode functions, IMF). В любой момент времени данные могут иметь множество сосуществующих внутренних колебаний — IMFs. Каждое колебание, линейное или нелинейное, представляет собой модовую функцию, которая имеет экстремумы и нулевые пересечения. Кроме того, колебания в определенной степени «симметричны» относительно локального среднего значения. Конечные сложные данные образуются суммой модовых функций, наложенных на региональный тренд сигнала.

Эмпирическая мода — это такая функция, которая обладает следующими свойствами:

1.                  Количество экстремумов функции (максимумов и минимумов) и количество пересечений нуля не должны отличаться более чем на единицу.

2.                  В любой точке функции среднее значение огибающих, определенных локальными максимумами и локальными минимумами, должно быть нулевым.

IMF представляет собой колебательный режим, но вместо постоянной амплитуды и частоты, как в простой гармонике, у IMF могут быть переменная амплитуда и частота, как функции независимой переменной (времени, координаты, и пр.). Первое свойство гарантирует, что локальные максимумы функции всегда положительны, локальные минимумы соответственно отрицательны, а между ними всегда имеют место пересечения нулевой линии. Второе свойство гарантирует, что мгновенные частоты функции не будут иметь нежелательных флуктуаций, являющихся результатом асимметричной формы волны.

Любую функцию и любой произвольный сигнал, изначально содержащие произвольную последовательность локальных экстремумов (минимум 2), можно разделить на семейство функций IMFs и остаточный тренд. Если данные лишены экстремумов, но содержат точки перегиба («скрытые» экстремумы наложения модовых функций и крутых трендов), то для открытия экстремумов может использоваться дифференцирование сигнала.

Схема преобразования Гильберта-Хуанга может быть разделена на две части. В первом шаге, экспериментальные данные разлагаются в ряд внутренних модовых функций (IMFs). Эта декомпозиция рассматривается как расширение данных в терминах внутренних модовых функций. Другими словами, эти внутренние модовые функции представлены как базис преобразования, которое может быть линейным или нелинейным, как диктуется по условиям. Так как IMFs имеют хорошие Гильбертовы преобразования, то могут быть вычислены соответствующие мгновенные частоты. Таким образом, в следующем шаге мы можем локализовать любое явление как во времени, так и на частотной оси. Локальная энергия и мгновенная частота, выведенная из IMFs, дают нам дистрибутивные «энергетические время-частотные» данные, и такое представление, определяемое как Гильбертов спектр.

Допустим, что имеется произвольный сигнал . Сущность метода EMD заключается в последовательном вычислении функций эмпирических мод  и остатков , где  при . Результатом разложения будет представление сигнала в виде суммы модовых функций и конечного остатка:

,                                                                                          (9)

где  — количество эмпирических мод, которое устанавливается в ходе вычислений.

Алгоритм эмпирической декомпозиции сигнала складывается из следующих операций его преобразования:

1.                  Находим в сигнале  положение всех локальных экстремумов, максимумов и минимумов процесса (номера точек  экстремумов), и значения  в этих точках (рис. 1). Между этими экстремумами сосредоточена вся информация сигнала. Группируем раздельно для максимумов и для минимумов массивы координат  и соответствующих им амплитудных значений . Число строк в массивах максимумов и минимумов не должно отличаться более чем на 1.

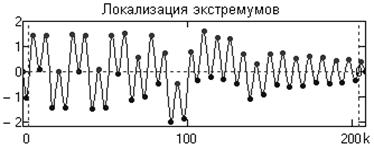
Рис. 1. Локализация экстремумов в сигнале.

2.                  Применяя сплайны (или каким либо другим методом) вычисляем верхнюю  и нижнюю  огибающие процесса соответственно, по максимумам и минимумам, как это показано на рис. 2. Определяем функцию средних значений  между огибающими (рис. 2).

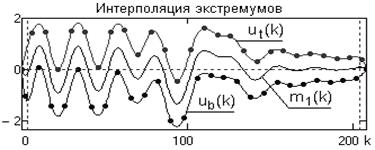
Рис. 2. Интерполяция экстремумов и построение огибающих

Определяем функцию средних значений  между огибающими.

,                                                                                                 (10)

Разность между сигналом  и функцией  дает нам первую компоненту отсеивания — функцию , которая является первым приближением к первой функции IMF:

,                                                                                                      (11)

3.         Повторяем операции 1 и 2, принимая вместо  функцию, и находим второе приближение к первой функции IMF — функцию .

,                                                                                                    (12)

Последующие итерации выполняются аналогичным образом:

,                                                                                                   (13)

По мере увеличения количества итераций функция  стремится к нулевому значению, а функция  — к неизменяемой форме.

Последнее значение  итераций принимается за наиболее высокочастотную функцию  семейства IMF, которая непосредственно входит в состав исходного сигнала . Это позволяет вычесть  из состава сигнала и оставить в нем более низкочастотные составляющие

,                                                                                                        (14)

На рис. 3 показано графическое представление вычитание из сигнала высокочастотной составляющей, сформированной по алгоритму, заданному (10)-(14).

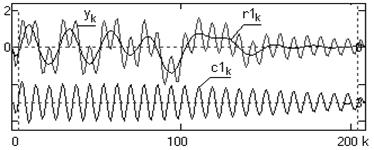
Рис. 3. Выявление низкочастотных составляющих в сигнале

Следующую внутреннюю модовую функцию найдем, повторив операции 1–3 декомпозиции, описанные выше, с той разницей, что входным сигналом является остаток . Шаги 1–3 могут быть повторены для всех последовательных , и результат будет представлять последовательность вычислений:

,                                                               (15)

Метод EMD закончен, когда остаток, в идеале, не содержит экстремумов. Это означает, что остаток — или константа или монотонная функция [13]. Извлеченные IMFs симметричны, имеют уникальные локальные частоты, различные IMFs не показывают ту же самую частоту в то же самое время. Другими словами, остановка декомпозиции сигнала должна происходить при максимальном «выпрямлении» остатка, т. е. превращения его в тренд сигнала по интервалу задания с числом экстремумов не более 2–3.

Из недостатков преобразования Гильберта-Хуанга отметим, что эмпирический процесс разложения сигнала в силу своей адаптивности не управляем, по крайней мере, в настоящей форме. Даже монотональные составляющие многокомпонентного сигнала при определенном влиянии дестабилизирующих факторов (шумов, импульсных помех и т. п.) и близких по частоте соседних компонент могут при декомпозиции «перетекать» на отдельных временных интервалах в модовые функции соседних IMF.

Обоснование выбора речевых признаков для обучения нейронной сети

Для успешного обучения нейронной сети необходимо корректным образом задавать параметры элементов обучающей выборки. В таком случае можно обеспечить высокое качество распознавания предъявляемых исходных данных.

В условиях фонемно-ориентированного подхода исходными данными для обучения сети и распознавания сигнала будут являться фонемы. Рассматривая фонему как сигнал во временной области, пользуясь тем или иным алгоритмом интегрального преобразования, можно получить необходимую информацию о его ключевых признаках требуемых для обучения.

Рассмотрим вопрос извлечения информационных признаков фонемы при применении преобразования Фурье. Как отмечается в [6; 9], одним из основных подходов к получению признаков, идентифицирующих особенности речи, является ее спектральное представление. Оконное преобразование Фурье позволяет анализировать поведение спектрального состава сигнала во времени. Оно хорошо подходит для анализа гласных фонем, т. к. базисные функции — тригонометрические периодические функции, а гласные звуки представляют собой почти-периодичные сигналы [7]. В исследовании производилось разбиение на сегменты шириной 50–200 Гц. Такой диапазон был подобран экспериментальным путем. Каждый из сегментов отвечал преобразованию Фурье во временной области, взятому с прямоугольным окном. В качестве признаков для нейронной сети выбирался вектор энергий сегментов преобразования Фурье.

При использовании вейвлет-преобразования для формирования признаков, описывающих речевой сигнал, необходимо определить число уровней детализации, соответствующее размеру анализируемого частотного диапазона. Например, вейвлет Добеши 8 имеет центральную частоту  Гц. При частоте дискретизации 22050 отсчетов в секунду, получаем центральную частоту вейвлета, используемого для первого уровня разложения [10].

                                                                (16)

С каждым следующим уровнем разложения частота вейвлета будет уменьшаться в два раза. Центральная частота вейвлета на десятом уровне разложения будет равна 28,7 Гц. Таким образом, вейвлет коэффициенты для десяти уровней разложения отражают характеристики сигнала в указанном частотном диапазоне речи. Коэффициенты вейвлет-разложения речевого сигнала (фонема «А») на семь уровней показаны на рис. 4.

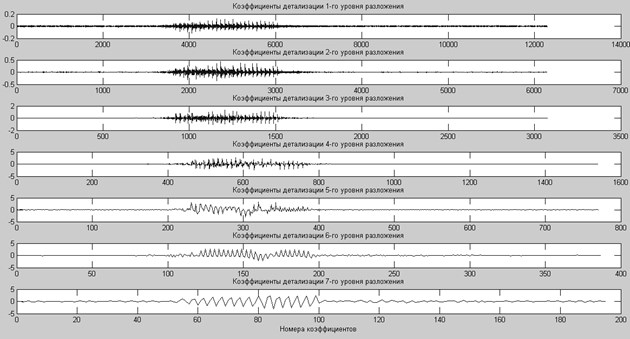
Рис. 4. Коэффициенты вейвлет-разложения речевого сигнала на семь уровней детализации

Оценим длину фиксированного интервала во временной области, на котором будут рассчитываться признаки речевого сигнала. Данный интервал должен быть меньше времени звучания фонемы. В русском языке длительности фонем изменяются в пределах 50-250 мс [7]. Значение длины сегмента должно позволять вычислять признаки речевого сигнала. Нижняя граница анализируемого частотного диапазона равна 28,7 Гц, в выделенный сегмент должен укладываться по крайней мере один период данной частотной составляющей, который равен 36 мс. Это значит, что длина сегмента, удовлетворяющая изложенным требованиям, будет равна 36 мс.

Таким образом, число уровней вейвлет-разложения сигнала фонемы зависит от частоты его дискретизации и типа вейвлета. В качестве признаков для обучения нейронной сети также была выбрана энергия вейвлет-разложения на каждом из уровней декомпозиции.

Преобразование Гильберта-Хуанга характерно тем, что в его результате образуется множество внутренних модовых функций (IMFs), отражающих нелинейные изменения, происходящие в сигнале (рис. 5). При этом каждая из них, в свою очередь, является временной функцией. Численные исследования, проведенные в работе показали, что параметры IMFs и их количество претерпевают существенные изменения даже в рамках какой-либо одной фонемы (в пределах выборки). В силу этого обстоятельства в качестве признаков для обучения нейросети выбирались энергии каждой из полученных эмпирических мод. Число входов нейронной сети, осуществляющей работу по распознаванию фонем с применением преобразования Гильберта-Хуанга, бралось равным числу IMFs.  При смешанном анализе к эмпирическим модам применялось вейвлет-преобразование.

Для каждой из фонем число IMFs, предъявляемых в качестве элементов обучающей выборки, подсчитывалось на этапе построения нейросети. В качестве мощности множества входов формируемой нейронной сети бралось максимальное количество IMFs, полученных для всех фонем из словаря. Число выходов нейросети принималось равным количеству распознаваемых речевых единиц.

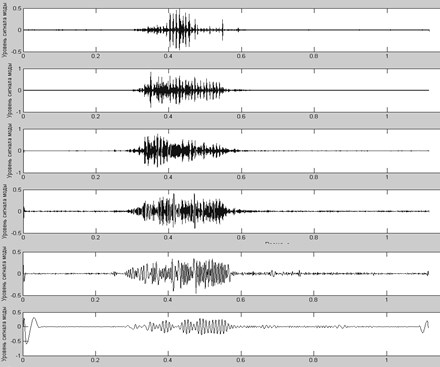
Рис. 5. Семейство первых шести эмпирических мод речевого сигнала.

Архитектура разработанного модуля

Для оценки эффективности описанных методов был разработан программный модуль преобразования русской речи в текст на основе фонемно-ориентированного и нейросетевого подхода. В модуле реализован синтез нейронных сетей (типа многослойный персептрон), обученных на основе различных признаков речевого сигнала, описанных выше. Это дает модулю высокую гибкость при работе с речевыми данными, а конечному пользователю предоставляет широкий выбор удобных для него настроек. Пользовательский интерфейс приложения для распознавания речи представлен на рис. 6.

Рис. 6. Пользовательский интерфейс приложения

Реализованы следующие функции:

1.      Открытие, запись, воспроизведение и сохранение сигналов в wav-формате;

2.      Выбор и настройка алгоритмов анализа данных. При этом допустимы следующие алгоритмы предварительной обработки звуковых сигналов:

2.1.  Вейвлет-преобразование сигнала.

2.2.  Оконное преобразование Фурье;

2.3.  Преобразование Гильберта-Хуанга.

В приложении также допускается смешанный анализ: так, преобразование Гильберта-Хуанга возможно использовать совместно с вейвлет-преобразованием.

3.      Создание, импорт, экспорт словаря фонем, формирование обучающей выборки.

Число входов нейросети определяется алгоритмом обработки сигнала, а число выходов определяется объемом словаря фонем.

Словарь нейронной сети представляет собой массив, состоящий из структур, каждая из которых состоит из имени фонемы, имени сигнала и массива данных, отвечающего фонеме. Данные в словаре нейронной сети представлены в виде таблицы, состоящей из названия сигнала, задаваемого вручную или автоматически, а также названия фонемы, которой данный сигнал отвечает.

4.      Создание, импорт нейронной сети, а также обучение и сохранение значений ее весов. Допускаются следующие алгоритмы обучения:

4.1.  Алгоритм обратного распространения ошибки;

4.2.  Генетический алгоритм.

Приложение поддерживает выбор типа активационной функции нейронов сети на этапе ее создания и обеспечивает задание числа нейронов скрытых слоев. При выборе доступны активационные функции следующего вида: сигмоидальная, функция Хевисайда, кусочно-линейная функция, функция Гаусса.

Для минимизации граничных эффектов при разбиении речи на фонемы допускается перекрытие фреймов. По умолчанию степень перекрытия составляет 25 %. Длительность звучания фонемы в составе речи составляет 15–50 мс [7]. По умолчанию в приложении длительность составляет 20 мс.

5.                  Выполнение автоматической очистки от шума и сегментации звуковых файлов с целью устранения пауз перед их распознаванием. Для больших возможностей анализа речи в приложении была предусмотрена возможность работы с фонемным словарем, на его основе формируется список фонем, который в дальнейшем используется при распознавании речи.

6.                  Осуществление фонетического анализа распознанного слова. Для фонетического анализа доступны алгоритмы Левенштейна и Дамерау-Левенштейна.

Как видно из описания, полученное решение наряду с обработкой мультимедийной информации, обеспечивает поддержку достаточно широкого спектра математических алгоритмов.

Для реализации пользовательского интерфейса был выбран язык C# и его библиотека Windows Forms. Windows Forms представляет собой технологию, используемую в Visual C# для создания интеллектуальных клиентских приложений на основе Windows, выполняемых в среде.NET Framework. Технология Windows Forms специально создана для быстрой разработки приложений, в которых необходимо наличие интуитивно понятного пользовательского интерфейса с гибкими возможностями.

Для языка программирования C# используется библиотека базовых типов среды.NET. Для организации типов (классов, структур, интерфейсов, встроенных типов данных и т. п.) в этой библиотеке используется концепция пространства имен. Вне зависимости от языка программирования, доступ к определенным классам обеспечивается за счет их группировки в рамках общих пространств имен [8]. Общий вид структуры среды.NET приведен на рис. 7.

В качестве инструмента для реализации математических расчетов использовался пакет MATLAB. Выбор был обусловлен тем, что среда MATLAB включает язык программирования высокого уровня, подсистему для визуализации графики, а также пакеты расширений для решения различных задач, в том числе и для обработки сигналов. Она также поддерживает разработку приложений как при использовании собственных средств компиляции и оптимизации кода, так и с применением современных сред разработки, таких, как RAD Studio и Visual Studio.

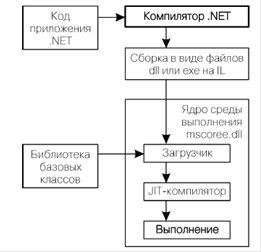
Рис. 7. Схема выполнения.NET-приложения

Компилятор MATLAB был применен для преобразования программ в приложения и библиотеки, которые могут работать независимо от самой системы MATLAB, а также поддерживает все ее особенности, включая объекты, частные функции и методы.

Интеграция MATLAB и библиотеки .NET осуществлялась с помощью пакета .NET Builder, который позволяет из набора m-функций создавать компоненты для .NET, используемых в разработке приложений на CLS_совместимых языках программирования. .NET Builder преобразовывает исходные функции  в .NET методы, которые инкапсулируют код MATLAB.

В основу реализации нейронной сети был положен функционал библиотеки Neural Network Library 0.1, распространяемой свободно и обладающей открытым исходным кодом. Для обработки звука наряду с возможностями MATLAB дополнительно использовалась библиотека NAudio.

Результаты исследования

Для моделирования распознавания слов и фонем средствами приложения была создана нейронная сеть, имеющая следующие параметры:

1.      Сеть обладала двумя скрытыми слоями, каждый слой содержал по 25 нейронов;

2.      Для нейронов в сети в качестве функции активации была выбрана сигмоидальная зависимость, как наиболее гладкая.

В качестве обучающей выборки использовалось множество {«В», «О», «А», «И», «С», «Ш»}. Каждой фонеме сопоставлялось 5–6 примеров звуковых фрагментов, озвученных различными дикторами.

Нейронная сеть обучалась с помощью алгоритма обратного распространения ошибки и генетического алгоритма.

Объяснение наличия достаточно большой погрешности, делающей нейросеть неприменимой для распознавания, может состоять в том, что в ряде случаев для некоторых фонем признаки в виде энергетических показателей сигнала могут оказаться недостаточно информативными. Качество обучения и распознавания в очень сильной зависимости от качества речевых единиц выборки. Для выполнения более детального анализа бралась уменьшенная выборка {«А», «В», «И», «О»}.

При применении генетических алгоритмов ошибка сети менялась более плавно. Стоит отметить, что вместе с тем особенности генетических алгоритмов не гарантируют того, что уровень ошибки может быть существенно ниже, чем в случае метода обратного распространения ошибки. Оптимальный подбор параметров генетического алгоритма с учетом параметров архитектуры нейронной сети требует отдельного исследования.

Наилучшие результаты при обучении на исходной выборке показали вейвлеты и комбинация преобразования Гильберта-Хуанга с вейвлетами. Время обучения сети с применением преобразования Гильберта-Хуанга существенно выше. Остальные алгоритмы на данной выборке не обеспечили удовлетворительного уровня ошибки обучения сети. С другой стороны, на уменьшенной выборке практически все алгоритмы обеспечили приемлемый результат. Это обусловлено тем, что гласные фонемы имеют почти-периодическое временное представление, как отмечалось ранее.

Звуковые фрагменты перед распознаванием проходили шумоочистку и сегментацию согласно алгоритму, предложенному в [11]. Временной интервал фреймов, на которые разбивался сегментируемый сигнал, составлял 20–40 мс. При распознавании фонем и слов результатом выступал нетранскрибированный вариант, а также конечная форма, получаемая после фонетического анализа.

В табл. 1–2 приведены результаты распознавания некоторых гласных фонем с применением вейвлетов (базис Добеши 8) и преобразования Гильберта-Хуанга и вейвлетов (базис Добеши 8).

Таблица 1

Результаты распознавания гласных фонем сетью, обученной на основной выборке с применением вейвлетов

Таблица 2

Результаты распознавания гласных фонем сетью, обученной на основной выборке с применением преобразования Гильберта-Хуанга и вейвлетов

Таблица 3

Сводные результаты распознавания фонем сетью, обученной на основной выборке с применением вейвлетов, %

є	А	О	И	В	С	Ш
1	100	95	98	100	86	90
2	92	95	100	100	100	100
3	95	89	90	98	99	97
Средний коэффициент распознавания	95	93	96	99,3	95	95,7
	95,7

Таблица 4

Сводные результаты распознавания фонем сетью, обученной на основной выборке с применением преобразования Гильберта-Хуанга и вейвлетов, %

є	А	О	И	В	С	Ш
1	100	95	100	99	100	85
2	90	88	90	99	100	100
3	92	90	95	100	92	89
Средний коэффициент распознавания	94	91	95	99,3	97,3	91,3
	94,7

Таблица 5

Сводные результаты распознавания фонем сетью, обученной на уменьшенной выборке с применением оконного преобразования Фурье, %

Таблица 6

Сводные результаты распознавания фонем сетью, обученной на уменьшенной выборке с применением преобразования Гильберта-Хуанга и вейвлетов, %

Из таблиц 1–2, 3–4 видно, что качество распознавания фонем у нейронных сетей, использующих признаки, вычисляемые по алгоритмам вейвлет-преобразования и преобразования Гильберта-Хуанга в сочетании с вейвлет-коэффициентами примерно одинаково (средние коэффициенты распознавания отличаются всего на 1 %). Скорость распознавания фонем у нейронных сетей не отличалась, но следует отметить, что время обучения сети, использующей вейвлет-коэффициенты, примерно в 2–3 раза меньше по сравнению с сетью, использующей преобразование Гильберта-Хуанга в сочетании с вейвлет-коэффициентами. Причина такой разницы в большой ресурсоемкости методов смешанного анализа.

Наряду с фонемами разработанный модуль тестировался в целях распознавания слов. Распознавание слов происходило с применением нейросетей, успешно обученных на исходной и уменьшенной выборках. Наилучшие результаты при распознавании показала сеть, обученная на основе признаков, полученных путем комбинированной обработки фонем с совместным применением преобразования Гильберта-Хуанга и вейвлетов. Вместе с тем на уменьшенной выборке, данная сеть работала не всегда стабильно по причине возможной избыточности информации, содержащейся в речевых признаках (таблица 6), а также в силу особенностей алгоритма, которые отмечались ранее. Лучшие результаты на ней дала сеть, обученная на основе преобразования Фурье (в таблице 5 приведены результаты распознавания фонем).

Заключение

В исследовании рассматривалась реализация модуля преобразования русской речи в текст, предназначенного для автоматизации ввода текстовой информации в ЭВМ.

Был описан нейросетевой подход к решению поставленной задачи. Произведен анализ способов получения признаков речевого сигнала с помощью вейвлет-преобразования, преобразования Фурье и преобразования Гильберта-Хуанга. Разработан метод формирования грамматической формы слова на основе его фонетического представления с использованием алгоритмов Левенштейна и Дамерау-Левенштейна. Построена база данных признаков эталонов фонем.

На основе представленных алгоритмов в среде Visual Studio на языке C# с выполнением интеграции с пакетом MATLAB был разработан модуль преобразования речи в текст. Приведено подробное описание компонентов и возможностей созданного программного обеспечения. Эксперименты по определению качества работы модуля показали, что одними из наиболее эффективных способов получения признаков на ограниченном множестве являются вейвлет-преобразование и преобразование Гильберта-Хуанга, дополненное вейвлет-преобразованием эмпирических мод. Требуются дополнительные исследования, связанные с поиском и введением новых методов получения речевых признаков, более полно характеризующих фонемы в различных частях слов, что позволит повысить качество распознавания.

Из полученных результатов можно сделать выводы о высокой эффективности применения нейросетевого подхода и фонемно-ориентированного подхода в задаче разработки данного модуля. Эксперименты показали достаточно высокий коэффициент распознавания речи.

Литература:

1.                  Астафьева Н. М. Вейвлет-анализ: основы теории и примеры применения. //Успехи физических наук. — 1996 — т. 166, № 11 — с. 1145–1170.

2.                  Давыдов А. В. Цифровая обработка сигналов: Тематические лекции. — Екатеринбург: УГГУ, ИГиГ, ГИН, Фонд электронных документов, 2005.

3. Дремин И. М., Иванов О. В., Нечитайло В. А. Вейвлеты и их использование. //Успехи физических наук. — 2001 — т. 171, № 5. — с. 465–500.

4.                  Дьяконов В. П., Абраменкова И. В. MATLAB. Обработка сигналов и изображений. Специальный справочник. — СПб.: «Питер», 2002. — С. 608.

5.                  Дьяконов В. П. Вейвлеты. От теории к практике. — 2-е изд. — М.: СОЛОН-Пресс, 2004. — 400 с.

6.                  Медведев М. С. Использование вейвлет-преобразования для построения моделей фонем руcского языка //Вестник КрасГУ. Серия физ.-мат. науки. — 2006. Вып. 9. — С. 193–201.

7.                  Михайлов В. Г., Златоустова Л. В. Измерение параметров речи. — М.: Радио и связь, 1987. — 168 с.

8.                  Смоленцев Н. К. Создание Windows-приложений с использованием математических процедур MATLAB. — М.: ДМК Пресс, 2008. — 456 с.

9.                  Фролов А. В. Синтез и распознавание речи. Современные решения / А. В. Фролов, Г. В. Фролов [Электронный ресурс]. — Режим доступа: http://www.frolov-lib.ru/books/hi/ch06.html

10.              Хармут X. Ф. Передача информации ортогональными функциями. — М.:Связь, 1975. — 272 с.

11.              Giannakopoulos T., “Study and application of acoustic information for the detection of harmful content, and fusion with visual information,” Ph.D. dissertation, Dpt of Informatics and Telecommunications, University of Athens, Greece, 2009.

12.              Huang N. E., Shen Z., Long S. R., Wu M. C., Shih H. H., Zheng Q., Yen N.-C., Tung С. C., and Liu H. H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. //Proceedings of R. Soc. London, Ser. A, 454. 1998 — P. 903–995.

13.              Qin S. R., Zhong Y. M. A new envelope algorithm of Hilbert–Huang Transform // Mechanical Systems and Signal Processing 20. 2006 — P. 1941–1952.

14.              The Hilbert-Huang transform and its applications / editors, Norden E. Huang, Samuel S. P. Shen. — World Scientific Publishing Co. Pte. Ltd. 5 Toh Tuck. Link, Singapore 596224.