Рассматривается пример решение задачи по определению всех видов передаточных отношений механизмов с замкнутой системой тел качения (ЗСТК) с диаметрами равной величины и зазором между телами качения при ведущем внутреннем кольце и вводе поправки в расчет геометрических параметров по дорожке качения наружного кольца.
Ключевые слова: механизм с замкнутой системой тел качения с диаметрами равной величины, механизм-прототип, эксцентриковый механизм качения, тела качения, сепаратор, дорожка качения, геометрические параметры, зазор между телами качения.
Передаточное отношение является одним из основных показателей, используемых при выборе механизмов приводов технологического оборудования. Достижение требуемых величин показателей качества технологического оборудования напрямую зависит от подбора каждого элемента привода, т. е. от правильно определенных видов передаточных отношений и диапазонов их значений. С целью расширения областей применения механизмов с замкнутой системой тел качения (ЗСТК) необходимо решить задачу по определению видов передаточного отношения механизмов данного вида, которые могут содержать в своей структуре тела качения с диаметрами как равной, так и разной величины. Механизм с ЗСТК с диаметрами равной величины является механизмом-прототипом для эксцентрикового механизма качения (ЭМК) как с зазором между телами качения, так и без данного параметра, который также может быть классифицирован как механизм с ЗСТК с диаметрами разной величины. Для ЭМК характерно смещение центров дорожек качения колец относительно друг друга на величину эксцентриситета и наличие замкнутой системы тел качения с диаметрами разной величины [1]. Тела качения механизмов данного вида могут обладать или гладкими рабочими поверхностями (фрикционные) [1…10] или поверхностями с выступами (зубчатые) [11…14]. Коллектив авторов проводит теоретические и экспериментальные исследования геометрических и кинематических параметров исполнительных механизмов технологического оборудования разработанного на базе механизмов данного вида с диаметрами разной (эксцентриковые) [1…4] или равной (соосные) [5…10] величины. В процессе реализации данных исследований было установлено, что задача по определению величин номинальных значений геометрических параметров механизмов с замкнутой системой тел качения равной величины является не линейной и при начальных условиях, что все исходные параметры постоянные величины и больше нуля может не иметь решения, т. е.
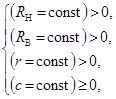 (1)
(1)
где RВ и RН — радиусы дорожек качения внутреннего и наружного колец; r — радиус тел качения; ![]() — зазор между телами качения.
— зазор между телами качения.
С целью исключения подобных ситуаций в работах [5…10] авторами сформированы области существования механизмов с ЗСТК с диаметрами равной величины как зазором между телами качения, так и без данного параметра. Для решения задачи по определению величин номинальных значений геометрических параметров при системе (1) необходим ввод поправки в расчет номинальных значений геометрических параметров, считая, что один из исходных параметров является величиной переменной. Вариация значениями радиуса тел качения и зазора не позволяет достичь требуемого результата. В этом случае получаем, что для решения данной задачи имеем два возможных направления ввода поправки в расчет геометрических параметров, т. е. либо ![]() , либо
, либо ![]() .
.
При вводе поправки по дорожке качения наружного кольца для механизма с ЗСТК с диаметрами равной величины и зазором система начальных условий (1) претерпит некоторые изменения
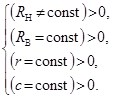 (2)
(2)
В соответствии с условием существования (сборки) механизмов с ЗСТК с диаметрами равной величины и зазором, которое сформулировано авторами в работах [4…6], число тел качения найдем как
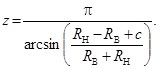 (3)
(3)
При принятых начальных условиях (2) и в соответствии с выбранным направлением ввода поправки в расчет номинальных значений геометрических параметров преобразование (3) позволит получить формулу для вычисления радиуса дорожки качения наружного кольца
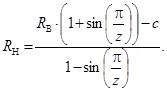 (4)
(4)
Механизмы с ЗСТК с диаметрами равной величины являются представителями эпициклических механизмов, следовательно, обладают тремя видами передаточного отношения: прямое, обратное и внутреннее, а также являются реверсивными, т. е. позволяют ведущему звену совершать вращательные движения, как по ходу часовой стрелки, так и в противоположном направлении. В зависимости от особенностей структуры связанных с сочетанием подвижных и неподвижных звеньев эпициклические механизмы данного вида являются либо планетарными, либо дифференциальными, которые могут работать в режиме редуктора (при ![]() ) или мультипликатора (при
) или мультипликатора (при ![]() ).
).
Рассмотрим пример решения задачи по определению всех видов передаточных отношений механизмов с замкнутой системой тел качения (ЗСТК) с диаметрами равной величины и зазором при ведущем внутреннем кольце, неподвижном наружном кольце и сепараторе (водило) в качестве выходного звена, считая, что движение звеньев совершается без скольжения (проскальзывания). Для этого составим расчетную модель (рис. 1) и примем следующие обозначения: ![]() ,
, ![]() — дорожки качения внутреннего и наружного колец; RВ, RН, ОВ и OН — радиусы и геометрические центры дорожек качения внутреннего и наружного колец; С — сепаратор (водило);
— дорожки качения внутреннего и наружного колец; RВ, RН, ОВ и OН — радиусы и геометрические центры дорожек качения внутреннего и наружного колец; С — сепаратор (водило); ![]() — зазор между телами качения; r0, r1, ri и
— зазор между телами качения; r0, r1, ri и ![]() ,
, ![]() ,
, ![]() — радиусы и углы положения тел качения.
— радиусы и углы положения тел качения.
Прямое передаточное отношение механизмов с ЗСТК с диаметрами равной величины и зазором при ведущем внутреннем кольце, неподвижном наружном кольце и сепараторе (водило) в качестве выходного звена получим, используя метод обращенного движения (формула Виллиса)
![]() (5)
(5)
где ![]() — внутреннее передаточное отношение механизма рассматриваемого вида при ведущем внутреннем кольце и неподвижном сепараторе (водило).
— внутреннее передаточное отношение механизма рассматриваемого вида при ведущем внутреннем кольце и неподвижном сепараторе (водило).
Внутреннее передаточное отношение механизма с ЗСТК с диаметрами равной величины и зазором
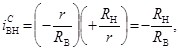 (6)
(6)
здесь ![]() , знаки «–» и «+» соответствуют внешнему и внутреннему контактам дорожек качения внутреннего и наружного колец с телами качения.
, знаки «–» и «+» соответствуют внешнему и внутреннему контактам дорожек качения внутреннего и наружного колец с телами качения.
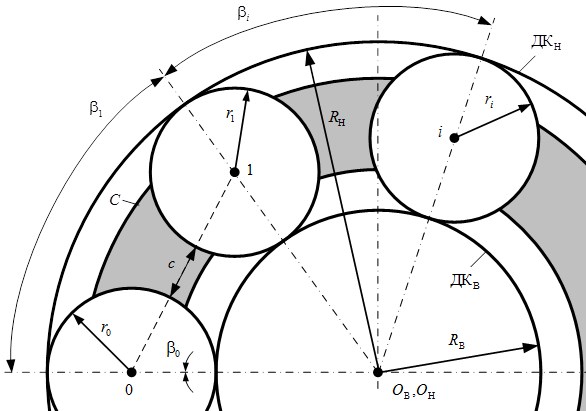
Рис. 1. Расчетная модель механизма с замкнутой системой тел качения с диаметрами равной величины и зазором
Подставив (4) в (6) и преобразовав, будем иметь
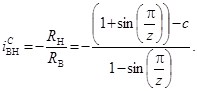 (7)
(7)
С учетом (7) преобразуем формулу (5) для прямого передаточного отношения механизма с ЗСТК с диаметрами равной величины и зазором в окончательный вид
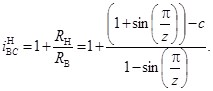 (8)
(8)
Обратное передаточное отношение механизма с ЗСТК с диаметрами равной величины и зазором имеет место при ведущем сепараторе (водило), остановленном наружном кольце и внутреннем кольце в качестве выходного звена, тогда с учетом (8) получим
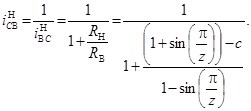 (9)
(9)
Варьируя числом тел качения в диапазоне (0…100) и значением радиуса дорожки качения наружного кольца в интервале (55…100) мм, проведем вычисления по выражениям (7)…(9) для всех видов передаточных отношений механизмов с ЗСТК с диаметрами равной величины и зазора ![]() . Расчет выполняем для начальных условий по системе (2). С целью повышения эффективности процесса вычислений авторами разработано программное обеспечение [15, 16], которое представляет собой программный комплекс «Эксцентрик» зарегистрированный в Реестре программ для ЭВМ Федеральной службы по интеллектуальной собственности (РОСПАТЕНТ) [17].
. Расчет выполняем для начальных условий по системе (2). С целью повышения эффективности процесса вычислений авторами разработано программное обеспечение [15, 16], которое представляет собой программный комплекс «Эксцентрик» зарегистрированный в Реестре программ для ЭВМ Федеральной службы по интеллектуальной собственности (РОСПАТЕНТ) [17].
Анализ результатов вычислений показывает, что изменение величины радиуса дорожек качения наружного кольца в выбранном интервале не оказывает влияния на диапазоны значений передаточных отношений механизмов рассматриваемого вида. По результатам вычислений, выполняем синтез диаграммы передаточных отношений (рис. 2).
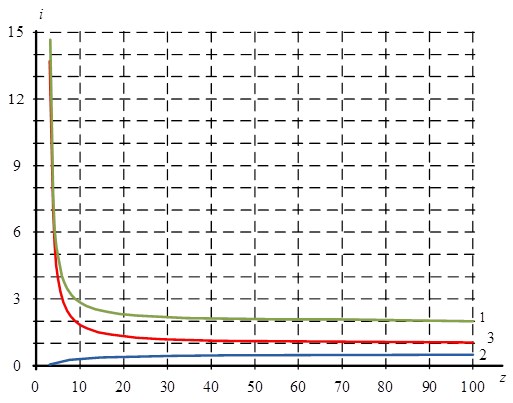
Рис. 2. Диаграмма передаточных отношений механизмов с ЗСТК с диаметрами равной величины и зазором при ведущем внутреннем кольце и вводе поправки по дорожке качения наружного кольца
1 — ![]() , 2 —
, 2 — ![]() , 3 —
, 3 — ![]()
Анализ диаграммы (рис. 2) показывает, что при вводе поправки по дорожке качения наружного кольца, а также ведущем внутреннем кольце, неподвижном наружном кольце и сепараторе (водило) в качестве выходного звена передаточные отношения механизмов с ЗСТК с диаметрами равной величины и зазором лежат в диапазонах: прямое ![]() , обратное
, обратное ![]() и внутреннее
и внутреннее ![]() . Это означает, что при данных условиях механизмы с ЗСТК с диаметрами равной величины и зазором являются редукторами, т. е. силовыми механизмами, так как
. Это означает, что при данных условиях механизмы с ЗСТК с диаметрами равной величины и зазором являются редукторами, т. е. силовыми механизмами, так как ![]() и
и ![]() . Наличие обратного передаточного отношения указывает на то, что при ведущем сепараторе (водило), неподвижном наружном кольце и внутреннем кольце в качестве выходного звена механизмы с ЗСТК при данных условиях находятся в режиме мультипликатора, т. е. являются кинематическими механизмами, так как
. Наличие обратного передаточного отношения указывает на то, что при ведущем сепараторе (водило), неподвижном наружном кольце и внутреннем кольце в качестве выходного звена механизмы с ЗСТК при данных условиях находятся в режиме мультипликатора, т. е. являются кинематическими механизмами, так как ![]() . Ввод поправки по дорожке качения наружного кольца существенно расширяет диапазон прямого передаточного отношения и увеличивает его значения, т. е. обеспечиваются максимально возможные величины передаточных отношений механизмов с ЗСТК с диаметрами равной величины и зазором.
. Ввод поправки по дорожке качения наружного кольца существенно расширяет диапазон прямого передаточного отношения и увеличивает его значения, т. е. обеспечиваются максимально возможные величины передаточных отношений механизмов с ЗСТК с диаметрами равной величины и зазором.
В результате выявлены все виды передаточных отношений механизмов с ЗСТК с диаметрами равной величины и зазором при ведущем внутреннем кольце, получены формулы для определения их величин, а также установлены возможные диапазоны их значений и режимы работы механизмов, что позволяет обеспечить достижение показателей качества приводов технологического оборудования.
Литература:
1. Мерко М. А. Кинематические и геометрические характеристики эксцентрикового механизма качения: автореф. дис. канд. техн. наук: 05.02.02. Красноярск, 2002. 26 с.
2. Мерко М. А., Меснянкин М. В., Шемякин Д. В., Леонтьев А. С., Собко И. В. Особенности формирования математической модели ЭМК при ведущем наружном кольце // Молодежь и наука: сборник материалов VII-ой Всероссийской научно-технической конференции студентов, аспирантов и молодых ученых посвященной 50-летию первого полета человека в космос [Электронный ресурс] / отв. ред. О. А. Краев — Красноярск: Сиб. фед. ун-т, 2011. — Режим доступа: http://conf.sfu-kras.ru/sites/mn2011/thesis/s19/ Shemyakin.pdf.
3. Меснянкин М. В., Мерко М. А., Колотов А. В., Беляков Е. В., Белякова С. А. Математическая модель ЭМК с сепаратором при ведущем внутреннем кольце // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2012. Т. 5. № 4. С. 62–67.
4. Мерко М. А., Меснянкин М. В, Беляков Е. В., Колотов А. В., Груздев Д. Е. Определение областей существования прототипа эксцентрикового механизма качения // Механики ХХI веку: сборник докладов VII-ой Всероссийская науч.-тенх. конф. с междунар. участием. Братск: БрГУ. 2008. С. 89–93.
5. Мерко М. А., Меснянкин М. В., Шевченко Е. С, Китура А. С. Формирование границ областей существования механизмов-прототипов ЭМК // Молодежь и наука: сборник материалов VIII Всероссийской научно-технической конференции студентов, аспирантов и молодых ученых, посвященной 155-летию со дня рождения К. Э. Циолковского [Электронный ресурс] / отв. ред. О. А. Краев — Красноярск: Сиб. федер. ун-т, 2012. — Режим доступа: http://conf.sfu-kras.ru/sites/mn2012/thesis/s017/s017–091.pdf.
6. Меснянкин М. В., Мерко М. А., Колотов А. В., Митяев А. Е. Определение границ областей существования механизмов-прототипов ЭМК при вводе поправки в расчет по дорожке качения внутреннего кольца // Вестник Красноярского государственного аграрного университета. 2012. № 12. С. 138–141.
7. Мерко М. А., Меснянкин М. В., Митяев А. Е. Описание математической модели механизма-прототипа ЭМК с сепаратором (водило) при ведущем внутреннем кольце // Молодой ученый. 2013. № 3. С. 71–75.
8. Мерко М. А., Меснянкин М. В., Колотов А. В. Определение координат звеньев механизма с замкнутой системой тел качания с диаметрами равной величины // Актуальные проблемы гуманитарных и естественных наук 2013.№ 3. С.68–73.
9. Мерко М. А., Меснянкин М. В., Колотов А. В. Формирование областей существования механизма с ЗСТК с диаметрами равной величины с сепаратором (водило) при вводе поправки по дорожке качения наружного кольца // Молодой ученый. 2013. № 4. С. 76–80.
10. Мерко М. А., Меснянкин М. В., Митяев А. Е., Колотов А. В. Анализ взаимозависимостей геометрических параметров эксцентрикового механизма качения // Вестник Красноярского государственного аграрного университета. 2012. № 11. С. 180–184.
11. Беляков Е. В., Меснянкин М. В, Мерко М. А., Колотов А. В., Груздев Д. Е. Эксцентриковый планетарный механизм // Механики ХХI веку: сборник докладов VII-ой Всероссийская науч.-тенх. конф. с междунар. участием. Братск: БрГУ. 2008. С. 87–89.
12. Беляков Е. В., Колотов А. В., Меснянкин М. В, Мерко М. А. Зубчатый планетарный механизм для воспроизведения требуемого сложного закона движения выходного звена // Проблемы механики современных машин: материалы V-ой международной конференции. Улан-Удэ: ВСГУТУ. 2012. Т.1 С. 3–6.
13. Беляков Е. В., Мерко М. А., Колотов А. В., Меснянкин М. В., Митяев А. Е. Обеспечение требуемого движения выходного звена эксцентрикового эпициклического механизма // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2012. Т. 5. № 4. С. 47–51.
14. Белякова С. А., Груздев Д. Е., Беляков А. Н., Мерко М. А., Меснянкин М. В., Колотов А. В. Применение дифференциального механизма для шлифования плоских поверхностей // Сборник научных трудов Sworld по материалам международной научно-практической конференции. 2012. Т. 5. № 4. С. 51–56.
15. Мерко М. А., Меснянкин М. В., Файзиев А. Н., Вацлавский Е. С. Повешение эффективности проектирования эксцентриковых механизмов приводов технологического оборудования на основе ЭМК // Молодежь и наука: сборник материалов VII-ой Всероссийской научно-технической конференции студентов, аспирантов и молодых ученых посвященной 50-летию первого полета человека в космос [Электронный ресурс] / отв. ред. О. А. Краев — Красноярск: Сиб. фед. ун-т, 2011. — Режим доступа: http://conf.sfu-kras.ru/sites/ mn2011/thesis/s19/Faiziev.pdf
16. Беляков Е. В., Колотов А. В., Мерко М. А., Меснянкин М. В. Применение САПР при исследовании эксцентрикового планетарного механизма // Современные технологии. Системный анализ. Моделирование. 2012. № 3. С. 109–112.
17. Свидетельство о государственной регистрации программы для ЭВМ № 2012614197. Программный комплекс «Эксцентрик» / Меснянкин А. В., Мерко М. А., Колотов А. В., Груздев Д. Е., Митяев А. Е., Беляков Е. В.; заявитель и правообладатель ФГАОУ ВПО «Сибирский федеральный университет»; заявка № 2012612100 от 22.03.12; зарегистрировано в Реестре программ для ЭВМ 12.05.12.







