Моделирование асинхронного двигателя с помощью магнитных и электрических схем замещения с двумя пазами на полюс и фазу

Данная работа является продолжением работ [1], [2] и [3]. В работе [4] рассматривалось моделирование двухполюсного асинхронного двигателя с числом пазов на полюс и фазу q = 1. В этом случае размерность квадратной матрицы А равна девяти. В данной работе с увеличением числа пазов на полюс и фазу до двух размерность квадратной матрицы А, как будет показано ниже, возрастет до пятнадцати, что существенно расширит требования к инструментарию при программировании. В данной работе будет представлено сравнение характеристик линейного асинхронного двигателя с разомкнутым магнитопроводом, приведенного в работе [3], с круговым асинхронным двигателем. В обоих случаях расчет проводился с помощью магнитных и электрических схем замещения.

В пакете учебных программ по матрицам при подготовке студентов к исследовательской работе данная статья, на наш взгляд, займет важной место.

На рис.1,а показана линейная развертка кругового асинхронного двигателя с одной парой полюсов (2р = 2) и двумя числами пазов на полюс и фазу (q = 2). На рис. 1,б дана его магнитная схема замещения, где токи и потоки на входе двигателя являются соответствующими токами и потоками на его выходе.

Запишем основные уравнения для «n»-ого участка схемы замещения.

Баланс магнитных напряжений магнитной цепи

 — контурные магнитные потоки;

 — магнитные сопротивления воздушных участков;

 — магнитодвижущая сила, созданная статорным током , протекающим по всем проводникам паза ();

– в шунтирующих зонах;

 — М. Д. С. тока ротора в стержне ().

Баланс М. Д. С. для «n»-го участка имеет следующий вид:

.

Отсюда ток в стержне ротора определится по следующему выражению:

                        .                            (1)

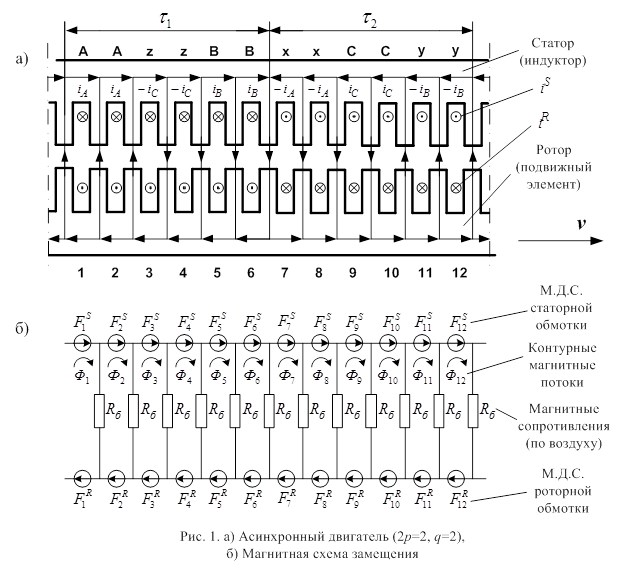
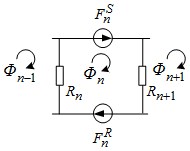
Рис. 2. Магнитная схема замещения

Уравнение баланса напряжений электрической цепи ротора

                                                                (2)

Выразим производные во времени через конечные разности:

,

где      n — номер зубцового деления;

k — номер шага разбиения по времени.

В формуле (2) скорость подвижного элемента принимаем равным  и в пределах «k» интервала считается постоянным.

Производные по пространственной координате «х» выразим через центральные конечные разности:

.

С учетом вышеприведенных замечаний уравнение (2) примет следующий вид:

                (3)

Исключим из уравнения (3) токи в роторе. Для этого подставим выражение (1) в уравнение (3) и получим:

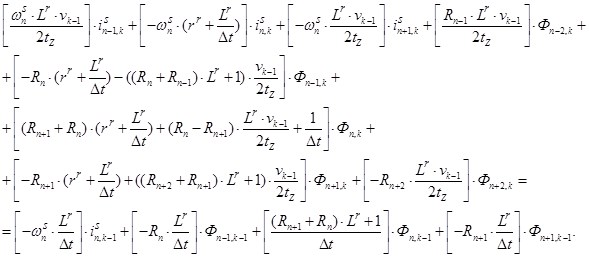      (4)

Это уравнение может быть реализовано при произведении матрицы А, элементы которой записаны в квадратных скобках, на матрицу-столбец из потоков (Ф) и токов статорной обмотки. Правая часть уравнения (4) формирует матрицу-столбец S из свободных членов в (k-1) момент времени. Матрица-столбец Х сформирована из первых двенадцати элементов, которые соответствуют потокам, а с 13 по 15 — токам i_А, i_В, i_С. Общий вид матриц при числе пазов на полюс и фазу q = 2 и числе полюсов 2р = 2 примет следующий вид:

Так как в асинхронном двигателе сопротивления на всех зубцовых делениях одинаковы R_n=R_б, то уравнение (4) примет следующий вид:

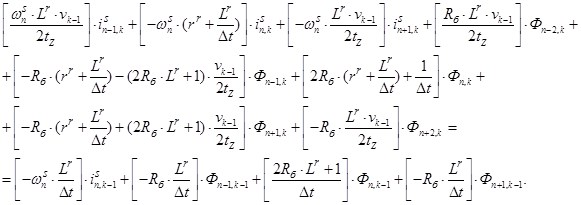        (5)

Введем следующие обозначения:

-        Элементы матрицы А, перемножаемые на потоки матрицы-столбца Х:

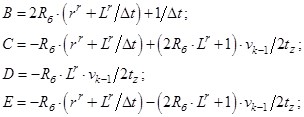
-                   Элементы матрицы А, перемножаемые на токи i_a, i_b, i_c матрицы Х:

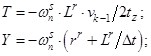
-                   Элементы матрицы-столбца свободных членов S:

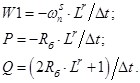
С учетом обозначений уравнение (5) примет следующий вид:

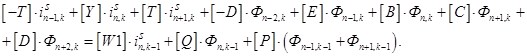   (6)

Уравнение (6) позволит определить для первых двенадцати строк элементы матрицы А и с первой по двенадцатый элементы матрицы-столбца S, для этого последовательно зададимся n:

n = 1.

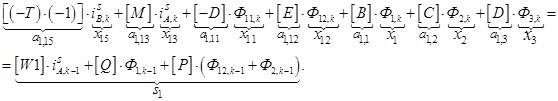
Запишем элементы матрицы А:

a_1,1=B; a_1,2=C; a_1,3=D; a_1,11=-D; a_1,12=E; a_1,13=М; a_1,15=T.

В правой части сформирован элемент s₁ матрицы-столбца S:

.

Примечание: Условно в начале обмотки принимаем знак «+», а в конце — «–», поэтому в элементе a_1,15 появилось умножение на (-1) в соответствии с рис.1,а.

n = 2.

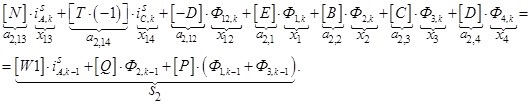
Отсюда элементы матрицы А:

a_2,1=E; a_2,2=B; a_2,3=C; a_2,4=D; a_2,12=-D; a_2,13=N; a_2,14=T• (-1).

Второй элемент s₂ матрицы-столбца S:

.

Аналогично, задаваясь n от 3 до 12 получим:

a_3,3= a_4,4= a_5,5= a_6,6=a_7,7= a_8,8= a_9,9= a_10,10=a_11,11= a_12,12=B;

a_3,4= a_4,5= a_5,6= a_6,7=a_7,8= a_8,9= a_9,10= a_10,11=a_11,12= a_12,1=С;

a_3,5= a_4,6= a_5,7= a_6,8=a_7,9= a_8,10= a_9,11= a_10,12=a_11,1= a_12,2=D;

a_3,2= a_4,3= a_5,4= a_6,5=a_7,6= a_8,7= a_9,8= a_10,9=a_11,10= a_12,11= a_1,12=E;

a_3,1= a_4,2= a_5,3= a_6,4=a_7,5= a_8,6= a_9,7= a_10,8=a_11,9= a_12,10= a_1,11= a_2,12=-D;

a_3,13= a_6,13= a_7,15= a_10,15=a_11,14=-T;

a_3,14= a_7,13= a_11,15=-M;

a_4,14= a_6,15= a_10,14=N;

a_5,14=a_8,14= a_9,13=a_12,13=a_4,15=T;

a_1,13=a_5,15=a_9,14=M.

Элементы матрицы-столбца свободных членов S:

;

;

;

;

;

;

;

;

;

.

Элементы 13 и 14 строк матрицы А и элементы s₁₃ и s₁₄ матрицы-столбца S формируются из баланса напряжения электрической цепи статорной обмотки. Если обмотка индуктора питается от трехфазного напряжения с соединением в «звезду» без нулевого провода, то

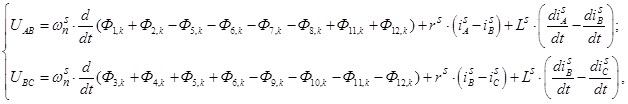        (7)

где   

С учетом шага по времени Δt в k-ый момент времени:

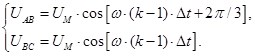
Уравнения (7) при выражении производных по времени через конечные разности примут следующий вид:

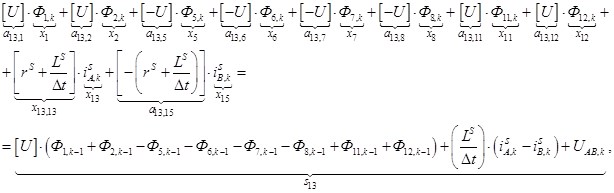
где

Обозначим r^s+L^s/Δt=KS, тогда

a_13,1= a_13,2= a_13,11= a_13,12=U;

a_13,5= a_13,6= a_13,7= a_13,8=-U;

a_13,13=KS;

a_13,15=-KS;

Правая часть определяет свободный член s₁₃ матрицы-столбца S:

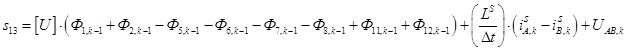
Аналогично, для второго уравнения (7) определим элементы 14 строки матрицы А и элемент s₁₄ матрицы-столбца S:

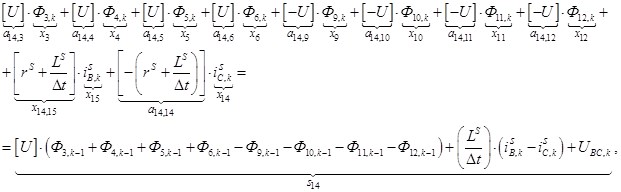
Тогда:

a_14,3= a_14,4= a_14,5= a_14,6=U;

a_14,9= a_14,10= a_14,11= a_14,12=-U;

a_14,14= -KS;

a_14,15=KS;

Правая часть определяет свободный член s₁₄ матрицы-столбца S:

.

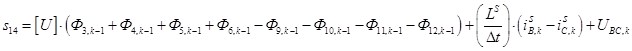Наконец, сумма токов определяет элементы пятнадцатой строки матрицы А и элемент s₁₅ матрицы-столбца S.

Окончательно, матрица А примет следующий вид, удобный для программирования в MatLab:

Неизвестные переменные (потоки и токи в статорной обмотке) в k-ый момент времени определяется в результате следующей операции с матрицами:

X=A^-1•S,

Далее, подставляя в уравнение (1) n = 1… 12, определяем токи в роторе:

Электромагнитные усилия на зубцовом делении определяются по следующим формулам:

          

          

          

    

Суммарное усилие:

Скорость в k-ый момент времени:

Произведем построение математической модели асинхронного двигателя методом Гаусса-Жордана с использованием языка программирования MatLab. Ниже приведен пример кода:

function AD_q_2

% Начальные условия

Rb=0.1003*10^7;

rs=19;

Ls=0.074;

rr=9.269*10^-5;

Lr=0.00372*10^-5;

dt=0.001;

tz=9.769*10^-3;

m=1.9;

v0=0;

wn=200;

f=50;

w=2*pi*f;

U=wn/dt;

Um=310;

X=zeros(15,1);

F=0;

K=input('длительность цикла k=');

for k=1:(K+1)

    v(1,k)=v0;                  % Создание вектор-строки для графика скорости

    f(1,k)=sum(F);              % Создание вектор-строки для графика усилия

    Uab=Um*cos(w*(k-1)*dt+2*pi/3);

    Ubc=Um*cos(w*(k-1)*dt);

% Заполнение матрицы А

A=zeros(15);

B=2*Rb*(rr+Lr/dt)+1/dt;

C=-Rb*(rr+Lr/dt)+(2*Rb*Lr+1)*v0/(2*tz);

D=-Rb*Lr*v0/(2*tz);

E=-Rb*(rr+Lr)-(2*Rb*Lr+1)*v0/(2*tz);

T=-wn*Lr*v0/(2*tz);

F1=-wn*(rr+Lr/dt);

M=F1+T;

N=-T+F1;

KS=rs+Ls/dt;

W=-wn*Lr/dt;

P=-Rb*Lr/dt;

Q=(2*Rb*Lr+1)/dt;

% Заполнение матрицы сопротивлений 

for n=1:12

    A(n,n)=B;

end;

for n=1:11

    A(n,n+1)=C;

    A(n+1,n)=E;

end;

for n=1:10

    A(n,n+2)=D;

    A(n+2,n)=-D;

end;

for n=1:2

    A(n,n+10)=-D;

    A(n+10,n)=D;

end;

A(1,12)=E;

A(12,1)=C;

% Заполнение столбцов 13,14 и 15 матрицы А

for n=1:2

    A(4-n,n+12)=-T;

    A(6-n,n+13)=T;

    A(10-n,n+12)=T;

    A(12-n,n+13)=-T;

    A(n,13)=(2-n)*M+(n-1)*N;

    A(n+2,14)=(n-2)*M+(1-n)*N;

    A(n+4,15)=(2-n)*M+(n-1)*N;

    A(n+5,13)=(n-2)*T+(1-n)*M;

    A(n+8,14)=(2-n)*M+(n-1)*N;

    A(n+10,15)=(n-2)*M+(1-n)*N;

end;

A(1,15)=T;

A(7,15)=-T;

A(8,13)=-N;

A(12,13)=T;

for n=1:2

   A(12+n,12+n)=((-1)^(n+1))*KS;

    A(12+n,15)=((-1)^n)*KS;

end;

for n=1:3

    A(15,n+12)=1

end;

% Заполнение строк 13 и 14 матрицы А

for n=1:4

    A(13,n+4)=-U;

    A(14,n+2)=U;

    A(14,n+8)=-U;

end;

for n=1:2

    A(13,n)=U;

    A(13,n+10)=U;

end;

% Матрица свободных членов

S=[W*X(13)+P*(X(12)+X(2))+Q*X(1);

   W*X(13)+P*(X(1)+X(3))+Q*X(2);

   W*(-1)*X(14)+P*(X(2)+X(4))+Q*X(3);

   W*(-1)*X(14)+P*(X(3)+X(5))+Q*X(4);

   W*X(15)+P*(X(4)+X(6))+Q*X(5);

   W*X(15)+P*(X(5)+X(7))+Q*X(6);

   W*(-1)*X(13)+P*(X(6)+X(8))+Q*X(7);

   W*(-1)*X(13)+P*(X(7)+X(9))+Q*X(8);

   W*X(14)+P*(X(8)+X(10))+Q*X(9);

   W*X(14)+P*(X(9)+X(11))+Q*X(10);

   W*(-1)*X(15)+P*(X(10)+X(12))+Q*X(11);

   W*(-1)*X(15)+P*(X(11)+X(1))+Q*X(12);

  (X(1)+X(2)-X(5)-X(6)-X(7)-X(8)+X(11)+X(12))*U+(Ls/dt)*(X(13)-X(15))+Uab;

  (X(5)+X(6)-X(11)-X(12)-X(9)-X(10)+X(3)+X(4))*U+(Ls/dt)*(X(15)-X(14))+Ubc;

   0];

% Решение методом Гаусса-Жордана

Z=rref([A S]);

X=Z(1:15,16:16);

% Матрица токов ротора

Ir=[-wn*X(13)-Rb*X(12)+2*Rb*X(1)-Rb*X(2);

-wn*X(13)-Rb*X(1)+2*Rb*X(2)-Rb*X(3);

-wn*(-1)*X(14)-Rb*X(2)+2*Rb*X(3)-Rb*X(4);

-wn*(-1)*X(14)-Rb*X(3)+2*Rb*X(4)-Rb*X(5);

-wn*X(15)-Rb*X(4)+2*Rb*X(5)-Rb*X(6);

-wn*X(15)-Rb*X(5)+2*Rb*X(6)-Rb*X(7);

-wn*(-1)*X(13)-Rb*X(6)+2*Rb*X(7)-Rb*X(8);

-wn*(-1)*X(13)-Rb*X(7)+2*Rb*X(8)-Rb*X(9);

-wn*X(14)-Rb*X(8)+2*Rb*X(9)-Rb*X(10);

-wn*X(14)-Rb*X(9)+2*Rb*X(10)-Rb*X(11);

-wn*(-1)*X(15)-Rb*X(10)+2*Rb*X(11)-Rb*X(12);

-wn*(-1)*X(15)-Rb*X(11)+2*Rb*X(12)-Rb*X(1)];

% Электромагнитное усилие

F=[(X(2)-X(12))*Ir(1)/(2*tz);

   (X(3)-X(1))*Ir(2)/(2*tz);

   (X(4)-X(2))*Ir(3)/(2*tz);

   (X(5)-X(3))*Ir(4)/(2*tz);

   (X(6)-X(4))*Ir(5)/(2*tz);

   (X(7)-X(5))*Ir(6)/(2*tz);

   (X(8)-X(6))*Ir(7)/(2*tz);

   (X(9)-X(7))*Ir(8)/(2*tz);

   (X(10)-X(8))*Ir(9)/(2*tz);

   (X(11)-X(9))*Ir(10)/(2*tz);

   (X(12)-X(10))*Ir(11)/(2*tz);

   (X(1)-X(11))*Ir(12)/(2*tz)];

% Скорость

v0=v0+(sum(F)/m)*dt;

end;

% Построение графиков

   k=0:(K);

   subplot(2,1,1);

   plot(k*dt,v);title('Скорость');

   xlabel('t, c');

   ylabel('v, м/c');

   grid on

   subplot(2,1,2);

   plot(k*dt,f);

   title('Электромагнитное усилие');

   xlabel('t, c');

   ylabel('F, H');

   grid on

end

Результаты моделирования представлены в таблице 1, а также на рис.3 и 4.

Таблица 1

Результаты расчета

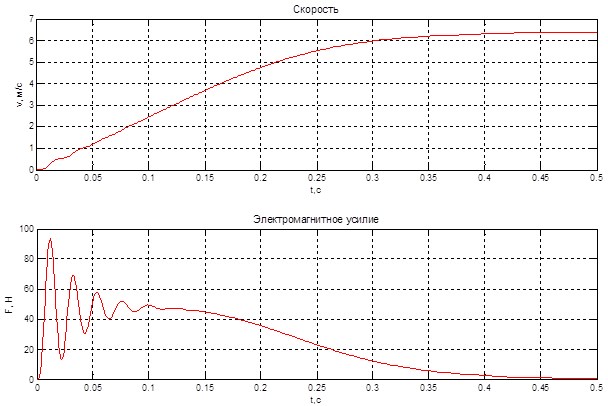
Рис. 3. Результат моделирования асинхронного двигателя в режиме прямого пуска

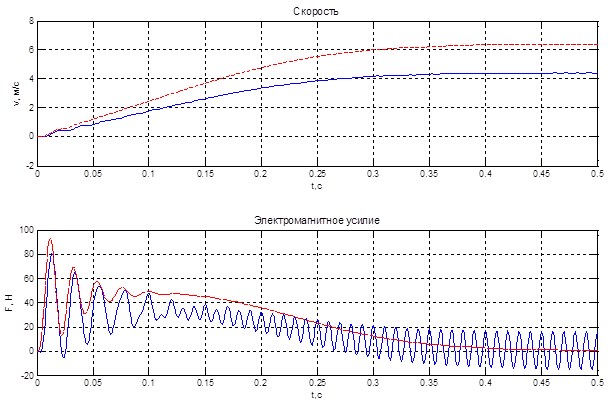
Рис. 4. Сравнение характеристик F(t) и v(t) линейного (--) и кругового (- - -)

асинхронных двигателей для 2р = 2 и q = 2

Как и следовало ожидать, в линейном асинхронном двигателе (рис.4) с увеличением скорости возрастают тормозные усилия от взаимодействия токов в подвижном элементе с неподвижным в пространстве и пульсирующим во времени потоками индуктора, возникающими вследствие разомкнутости магнитопровода. Это, в свою очередь, приводит к снижению скорости подвижного элемента (ротора), как это и было отмечено в [1].

Литература:

1.         Сарапулов Ф. Н., Емельянов А. А., Иваницкий С. В., Резин М. Г. Исследование электромеханических переходных процессов линейного асинхронного короткозамкнутого двигателя // Электричество. — 1982. — № 10. — С. 54–57.

2.         Емельянов А. А., Богатов Е. А., Клишин А. В., Медведев А. В., Симонович В. Г. Математическая модель линейного асинхронного двигателя на основе магнитных схем замещения // Молодой ученый. — 2010. — № 5. — С.14–22.

3.         Емельянов А. А., Медведев А. В., Богатов Е. А., Кобзев А. В., Бочкарев Ю. П. Программирование линейного асинхронного двигателя в MATLAB // Молодой ученый. — 2013. — № 3. — С. 129–143.

4.         Емельянов А. А., Медведев А. В., Кобзев А. В., Бочкарев Ю. П., Евдокимов О. В. Моделирование асинхронного двигателя с помощью магнитных и электрических схем замещения // Молодой ученый. — 2013. — № 4. — С. 1–10.

5.         Ануфриев И. Е. и др. MATLAB 7 / Ануфриев И. Е., Смирнов А. Б., Смирнова Е. Н. — СПб.: БХВ-Петербург, 2005. — 1104 с.