Общеизвестна важная роль, которую играют в теории волн соотношения Крамерса-Кронига, связывающие вещественную и мнимую часть диэлектрической проницаемости вещества (или вещественную и мнимую часть его диэлектрической восприимчивости, или вещественную и мнимую часть его показателя преломления, см. [1–3]). Универсальность этих соотношений связана с тем, что они следуют непосредственно из принципа причинности и для их применения не требуется сведений о микроскопической картине процессов, происходящих в веществе при взаимодействии с электромагнитным излучением.
К сожалению, применение этих соотношений в точной формулировке требует информации о поведении диэлектрической проницаемости при изменении частоты от минус до плюс бесконечности. В данной статье предложен приближенный аналог соотношений Крамерса-Кронига, пригодный для изучения связи вещественной и мнимой части диэлектрической восприимчивости вещества вблизи изолированной спектральной линии.
Будем исходить из соотношений Крамерса-Кронига для диэлектрической восприимчивости вещества ![]() в формулировке [2]:
в формулировке [2]:
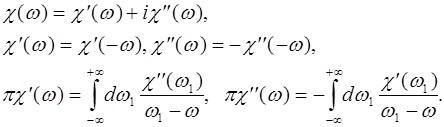 (П.1)
(П.1)
Интегралы в (П.1) понимаются в смысле главного значения. Введя в рассмотрение центральную частоту спектральной линии ![]() и отстройку от нее
и отстройку от нее ![]() , в предположении
, в предположении ![]() нетрудно вместо (П.1) получить соответствующие приближенные «низкочастотные» выражения
нетрудно вместо (П.1) получить соответствующие приближенные «низкочастотные» выражения
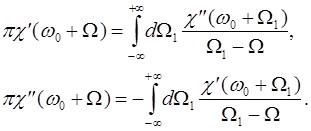 (П.2)
(П.2)
Физический смысл соотношений (П.2) совершенно очевиден и сводится к требованию выполнения принципа причинности не для произвольного сигнала (как в соотношениях (П.1)), а для его комплексной огибающей (при частоте несущей ![]() ).
).
Избавиться от интегрирования в смысле главного значения в (П.2) можно за счет появления неопределенности ![]() под знаком интеграла:
под знаком интеграла:
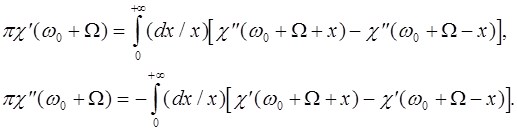 (П.3)
(П.3)
В соотношениях (П.3) сходимость интегралов на нижнем пределе интегрирования обеспечена ограниченностью подынтегральной функции, а на верхнем — её стремлением к нулю быстрее, чем по закону ![]() .
.
Далее будем для определенности говорить о газе с показателем преломления [1–3]
![]() (П.4)
(П.4)
где ![]() — комплексная диэлектрическая восприимчивость газа. Тогда, введя в рассмотрение коэффициент ослабления света по амплитуде
— комплексная диэлектрическая восприимчивость газа. Тогда, введя в рассмотрение коэффициент ослабления света по амплитуде
![]() (П.5)
(П.5)
и нормированный на 1 в центре спектральной линии ![]() комплексный форм-фактор линии
комплексный форм-фактор линии ![]()
![]() (П.6)
(П.6)
нетрудно переформулировать соотношения Крамерса-Кронига в форме (П.2) или (П.3) как соотношения для связи вещественной и мнимой части комплексного форм-фактора спектральной линии ![]() :
:
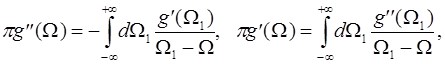 (П.7)
(П.7)
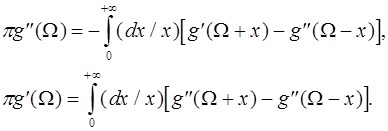 (П.8)
(П.8)
Соотношения (П.7) или (П.8) позволяют по вещественной части форм-фактора линии (то есть по контуру поглощения) определить ее мнимую часть, то есть изменение показателя преломления газа на частотах вблизи спектральной линии, обусловленное поглощением (или усилением) излучения вблизи спектральной линии.
Применим соотношения (П.7),(П.8) для трех типичных форм-факторов спектральных линии [2,3] — лоренцева (L), когда профиль линии определяется радиационным или столкновительным уширением, гауссова (G), когда профиль линии определяется доплеровским уширением, и «времяпролетного» (T), когда профиль линии определяется ограниченностью времени взаимодействия излучения с веществом.
Для вещественной части форм-фактора линии в этих случаях имеем (см. [2,3]):
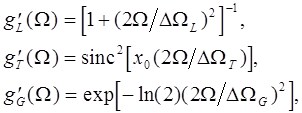 (П.9)
(П.9)
где ![]() — корень уравнения
— корень уравнения ![]() (
(![]() ), параметры
), параметры ![]() и
и ![]() — ширины вещественной части форм-факторов линий (
— ширины вещественной части форм-факторов линий (![]() ) на уровне 1/2 от максимума. Зависимость этих параметров от свойств среды приведена, например, в [2,3].
) на уровне 1/2 от максимума. Зависимость этих параметров от свойств среды приведена, например, в [2,3].
С использованием соотношений (П.7),(П.8) для мнимой части форм-факторов линий нетрудно получить
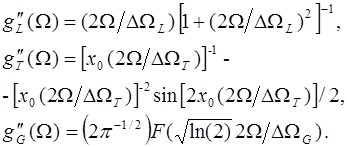 (П.10)
(П.10)
В итоге для комплексных форм-факторов линий имеем
 (П.11)
(П.11)
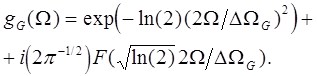
Для лоренцева форм-фактора линии полученные соотношения находятся, как и следовало ожидать, в полном соответствии с «микроскопическим» рассмотрением (см. [1–3]). Использованная в (П.10) и (П.11) функция
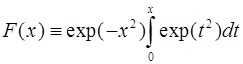 (П.12)
(П.12)
табулирована и называется интегралом Досона [4]. Ее асимптотическое поведение при больших или малых значениях аргумента определяется соотношениями [4] ![]()
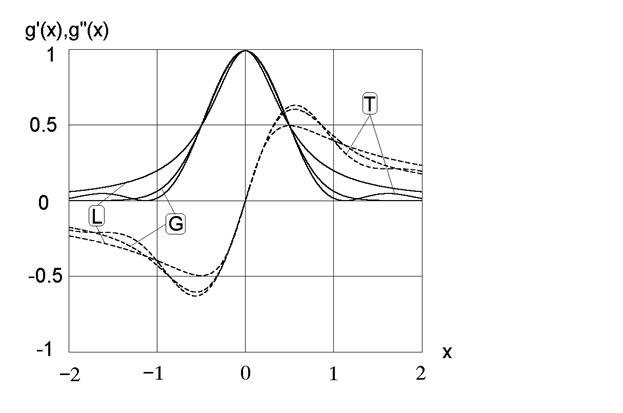
Рис. П.1. Зависимость вещественной ![]() (сплошная линия) и мнимой
(сплошная линия) и мнимой ![]() (пунктир) части форм-фактора спектральной линии от безразмерной частоты
(пунктир) части форм-фактора спектральной линии от безразмерной частоты ![]() (для лоренцева форм-фактора),
(для лоренцева форм-фактора), ![]() (для гауссова форм-фактора),
(для гауссова форм-фактора), ![]() (для времяпролетного форм-фактора). Буквой L обозначены вещественная и мнимая часть лоренцева форм-фактора линии, буквой G — гауссова, буквой T — времяпролетного форм-фактора.
(для времяпролетного форм-фактора). Буквой L обозначены вещественная и мнимая часть лоренцева форм-фактора линии, буквой G — гауссова, буквой T — времяпролетного форм-фактора.
Графики вещественной и мнимой части комплексных форм-факторов спектральной линии в случае лоренцева, гауссова и времяпролетного контуров спектральной линии приведены на рис. П.1. На этом рисунке по оси абсцисс отложена нормированная частота ![]() ,сплошной линией обозначены вещественные части форм-факторов линий, а пунктиром — мнимые.
,сплошной линией обозначены вещественные части форм-факторов линий, а пунктиром — мнимые.
Совпадение вещественных частей форм-факторов линий при ![]() не удивительно и связано просто с нормировкой ширины форм-факторов на единицу. Более интересным представляется почти точное совпадение мнимых частей форм-факторов линий при малых значениях параметра
не удивительно и связано просто с нормировкой ширины форм-факторов на единицу. Более интересным представляется почти точное совпадение мнимых частей форм-факторов линий при малых значениях параметра ![]() , то есть вблизи центра спектральной линии. Видно также, что «осцилляционный» характер контура поглощения линии при времяпролетном механизме уширения линии «передается» и мнимой части форм-фактора спектральной линии. Можно также отметить, что вблизи линии поглощения столкновительный механизм уширения линии (лоренцев контур) обеспечивает меньшее изменение вещественной части показателя преломления, чем доплеровский (гауссов профиль линии) или времяпролетный. Вдали от спектральной линии ситуация меняется на противоположную.
, то есть вблизи центра спектральной линии. Видно также, что «осцилляционный» характер контура поглощения линии при времяпролетном механизме уширения линии «передается» и мнимой части форм-фактора спектральной линии. Можно также отметить, что вблизи линии поглощения столкновительный механизм уширения линии (лоренцев контур) обеспечивает меньшее изменение вещественной части показателя преломления, чем доплеровский (гауссов профиль линии) или времяпролетный. Вдали от спектральной линии ситуация меняется на противоположную.
Тем не менее в любом из трех рассмотренных случаев (а не только в случае лоренцева контура линии) мнимая часть форм-фактора линии (то есть вещественная часть диэлектрической восприимчивости) при удалении от линии спадает весьма медленно — по гиперболическому закону ![]() , что и является основным выводом проведенного рассмотрения.
, что и является основным выводом проведенного рассмотрения.
Литература:
1. Виноградова М. Б., Руденко О. В., Сухоруков А. П. Теория волн.М.: Наука, 1979. 383 с.
2. Клышко Д. Н. Физические основы квантовой электроники. М.: Наука, 1986. 296 с.
3. Карлов Н. В. Лекции по квантовой электронике. М.: Наука, 1983. 320 с.
4. Справочник по специальным функциям / Под ред. М. Абрамовица и И. Стиган. М.: Наука, 1979. 832 с.







