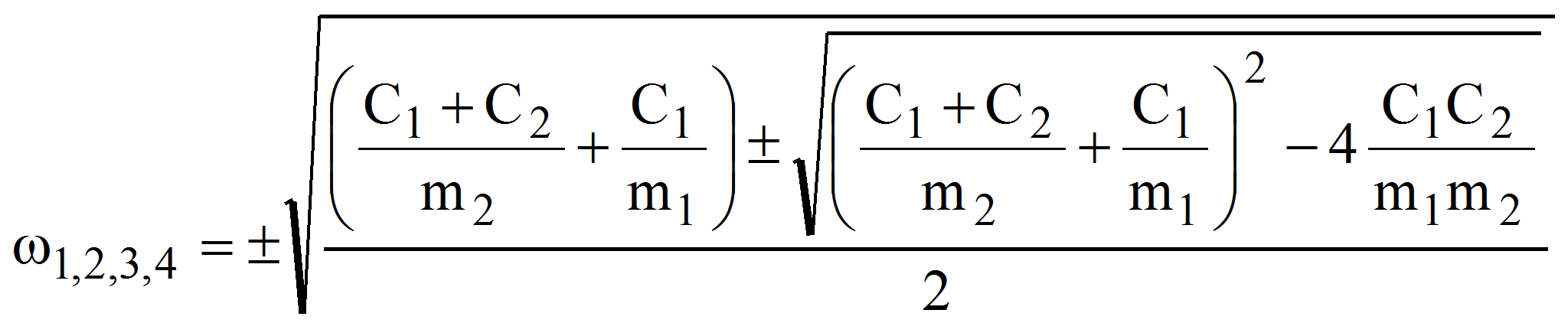Проблема аварийности на автотранспорте имеет важную роль в последнее десятилетие в связи с несоответствием существующей дорожно-транспортной инфраструктуры потребностям общества и государства в безопасном дорожном движении, недостаточной эффективностью функционирования системы обеспечения безопасности дорожного движения, крайне низкой дисциплиной участников дорожного движения [1, 10, 11].
Мероприятия, позволившие добиться снижение аварийности на автомобильных дорогах, связаны с внедрением, прежде всего, с принудительным ограничением скорости автотранспортных средств (АТС) в местах повышенной опасности [2]. Одним из путей решения этой проблемы является создание конструктивных элементов на дорожной одежде, способствующих генерации колебаний транспортных средств в режимах некомфортного восприятия водителем условий движения, что ведет к изменению параметров движения по направлению и скорости. Для выбора оптимальных параметров такой конструкции необходимы математические модели, включающие в себя особенности тактильного восприятия водителем наличия виброполосы, характеристики автотранспортных средств, скорость движения, общую длину полосы, глубину, ширину и шаг неровностей, материалы элементов конструкции виброполосы, дорожного покрытия и основания [3].
Виброполоса является конструктивным элементом дороги и в свою очередь определяет совокупные транспортно — эксплуатационные характеристики участка ее расположения, на котором этот элемент является средством снижения риска возможного дорожно-транспортного происшествия.
При наличии неровностей на поверхности автомобильной дороги в виде виброполосы, проведенные нами исследования позволяют определить основные ее параметры при движении АТС со скоростью 60 км/ч и шагом неровностей виброполосы 200 мм: глубина конструктивного элемента виброполосы 20…30 мм, ширина полосы может быть принята 150…200 мм, длина виброполосы выбирается в зависимости от продольного и поперечного профилей автомобильной дороги. С ростом скорости движения автомобиля и уменьшением длины волны неровностей существенного влияния глубины конструктивного элемента не наблюдается, что позволяет принять этот параметр на уровне 40 мм. При этом достигаются виброускорения в пределах 2,1 м/с2.
На следующем этапе рассматривается вибронагружение дорожной конструкции в следствие движения АТС по виброполосе. Принимая принципы расчета линейных упругих систем, рассмотрим динамическую модель дорожной конструкции и виброполосы с одной степенью свободы, с учетом вязко — упругих свойств материалов конструкции. Диссипативные силы принимаются пропорциональными скоростям. Ударный импульс представлен в форме полуволны синусоиды и из спектра нагрузки выделены частоты 8…20 Гц.
Действующие нагрузки являются квазистационарными с полимодальным распределением вероятностей. Накопленные остаточные деформации не определяются какой-либо одной нагрузкой, и характеризуются всей их совокупностью с учетом стохастичности. В связи с этим требуется разработка методики учета всех разновидностей режимов нагружения по долям их участия в формировании основных статистик распределения вероятности воздействий в каждом сегменте пути [4].
Определим единичное перемещение основания по зависимости [5]:
где P0, —
параметры
нагрузки; Q, ξ,
![]() ,
,
![]() —
параметры
процесса; t —
время; m —
активная масса.
—
параметры
процесса; t —
время; m —
активная масса.
где
![]() —
коэффициент поглощения строительных материалов 0,25;
—
коэффициент поглощения строительных материалов 0,25;
![]() —
частота внешней силы;
—
частота внешней силы;
![]() —
собственная частота; С — жесткость; К —
коэффициент согласования 1,13; F —
площадь штампа.
—
собственная частота; С — жесткость; К —
коэффициент согласования 1,13; F —
площадь штампа.
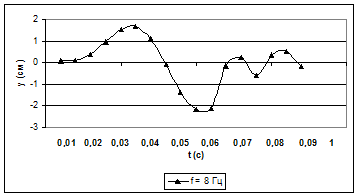
По разработанной математической модели были проведены имитационные расчеты перемещений дорожного покрытия (рис. 1). Колебания носят затухающий характер при расчетном коэффициенте затухания. Максимальное значение амплитуды перемещения наблюдается при t = 0,02–0,03 с.
Рис. 1. График зависимости динамического прогиба от времени при Е = 200 кг/см2
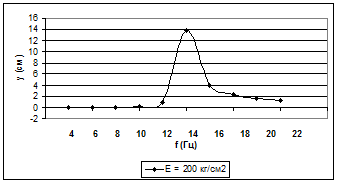
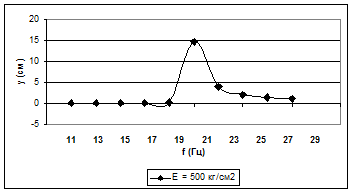
Полимодальное действие внешней нагрузки представлено на рис. 2, 3. По результатам расчетов отметим, что в системе имеет место резонанс, например, при Е = 200 кг/см2 и t = 0,01 с резонанс наступает при частоте 14 Гц. При Е = 500 кг/см2 резонанс смещается в сторону увеличения частоты и наблюдается при частоте 21 Гц.
Рис. 2. График зависимости динамического прогиба от частоты нагружения при Е = 200 кг/см2
Рис. 3. График зависимости динамического прогиба от частоты нагружения при Е = 500 кг/см2
Проведены также расчеты статического модуля упругости по формуле:
где Р — давление
в месте контакта; D —
диаметр эквивалентного штампа;
![]() —
коэффициент Пуассона материала основания; y —
прогиб.
—
коэффициент Пуассона материала основания; y —
прогиб.
Результаты расчетов
приведены на рис. 4. В качестве примера рассмотрено отношение
динамического модуля к статическому при действии нагрузки 25 кН
с частотой 8 Гц. Это отношение составило
![]() .
В работе [6] указано, что с ростом скорости движения с 10
до 130 км/ч динамический модуль упругости может вырасти в 12 раз,
а напряжение сжатия на поверхности основания могут увеличиться
больше, чем на 20 %.
.
В работе [6] указано, что с ростом скорости движения с 10
до 130 км/ч динамический модуль упругости может вырасти в 12 раз,
а напряжение сжатия на поверхности основания могут увеличиться
больше, чем на 20 %.
Рис. 4. Статический модуль основания в функции прогиба
В работе также рассмотрена двухмассовая модель дорожной конструкции для динамической идентификации деформационного состояния дорожной конструкции при свободных колебаниях [7, 8, 9]:
где m1 и m2 — массы верхнего и нижнего слоя; С1 и С2 — коэффициент жесткости дорожного покрытия и основания; у1 и у2 — перемещение первой и второй масс.
Если виброперемещения представить в виде у1=А1sin(ωt+φ1) и у2=А2sin(ωt+φ2), то соответствующие преобразования дают соотношение для определения собственных частот:
Методика расчета реализована при допущении: формирование жесткостей слоев С1 и С2 до расчетного значения происходит во времени намного большее, чем время действия штатной или тестовой нагрузки.
Для определения амплитуд колебаний двухмассовой системы без учета затухания представим решения дифференциальных уравнений движения в виде:
где
![]() -
амплитуды колебаний по обеим гармоникам;
-
амплитуды колебаний по обеим гармоникам;
![]() -
фазы колебаний.
-
фазы колебаний.
Для определения
коэффициентов
![]() воспользуемся
отношением амплитуд составляющих гармоник, соответственно для первой
и второй частоты:
воспользуемся
отношением амплитуд составляющих гармоник, соответственно для первой
и второй частоты:
Для исследование влияния параметров состояния слоев основания дороги на спектр собственных колебаний конструкций воспользуемся пакетом программ Mathcad.
Результаты моделирования колебаний дорожного покрытия и слоев основания с учетом динамической жесткости дорожной конструкции приведены на рис. 5, из которого видно, что перемещение слоев происходит в противофазе (относительная влажность w/w0 = 0,5 %, Еу — модуль упругости основания).
Рис. 5. Результаты расчетов вибрационных перемещений слоев дорожной конструкции
Математическая модель и результаты расчетов являются составной частью программного обеспечения диагностических процедур оценки динамического модуля материалов дорожной конструкции в режимах их нагружения АТС движущихся по виброполосе [12]. Это является основой разработки метода оценки, прогнозирования и повышения эффективности функционального назначения виброполосы для достижения цели снижения ДТП при анализе деформативности дорожной конструкции.
Литература:
Кычкин В. И., Юшков В. С. Математическая модель создания некомфортных условий при движении автомобиля по виброполосе // «Инновации в науке». Часть I г. Новосибирск 2012 г. С 73–80.
Илиополов С. К., Селезнев М. Г., Углова Е. В. Динамика дорожных конструкций. Ростов Н/Д: Рост. гос. строит. ун-т, 2002. — 258 с.
Смирнов А. В., Андреева Е. В., Кузин Н. В. Гашение колебаний и резонанс в дорожных конструкциях // М.: Наука и техника в дорожной отрасли. № 3–2006. С. 39–41.
Кычкин В. И., Мунасипов И. И. Разработка и исследование математической модели вибродиагностики подшпального основания трамвайных путей // Вестник ПНИПУ. — 2012 № 1. — С. 119–127.
Саргсян А. Е. Строительная механика. Механика инженерных конструкций: Учеб. для вузов / А. Е. Саргсян. — М.: Высш. шк., — 462 с.
Zhao Yan — ging, Yu Xin, Tan Yi — giu Beijing gongye daxue xuebao // J. Beijing Univ. Technol. 2010. 36, № 9, с. 1253–1257.
Кычкин В. И., Юшков В. С. Перспективный метод отраслевой системы вибродиагностики автомобильных дорог // Журнал «Молодой ученый» № 11 Чита 2012 г. С. 65–68.
Кычкин В. И., Юшков В. С. Неразрушающий динамический метод контроля дорожных одежд // Интернет-журнал «Науковедение». 2013 № 1 (14) [Электронный ресурс].- М. 2013. — Режим доступа: http://naukovedenie.ru/sbornik14/34tvn113.pdf.
Юшков Б. С., Юшков В. С., Кычкин В. И. Конструктивные особенности виброполосы в качестве дорожной разметки // Журнал «Народное хозяйство. Вопросы инновационного развития». Изд-во МИИ наука Москва № 2 2012 г. С. 71–75.
Юшков В. С. Новые подходы по нанесению горизонтальной дорожной разметки // Приволжский научный вестник № 2. Издательский центр Научного просвещения. Ижевск 2012 г. С. 17–19.
Юшков В. С. Шумовые полосы для снижения аварийности на автомобильных дорогах // Журнал «Молодой ученый» № 3 Чита 2012 г. С. 86–87.
Юшков Б. С., Кычкин В. И., Юшков В. С., Отчик Е. А. Разработка математической модели взаимодействия автомобиля и шумовой полосы // Вестник ПНИПУ «Охрана окружающей среды, транспорт, безопасность жизнедеятельности» № 2 Пермь 2012 г. С. 79–85.