В основе рассматриваемого соединения лежит деревянный элемент (доска, брус) [1] с вклеенными в него с двух противоположных сторон шайбами. Усилие на элемент передаются через сдвиговые силы, действующие непосредственно на шайбы. В общем случае в соединении могут быть либо один такой элемент (при присоединении его к узлу с помощью стальных накладок), либо несколько, когда в узел сходится два, три или более элементов с вклеенными шайбами. В работах [1,2,3,4,5] отмечалось что, экспериментальные исследования показали, работу соединений с передачей усилия через стальные пластины или посредством смежных с двух сторон деревянных элементов с вклеенными шайбами практически не отличаются между собой. Поэтому для достижения поставленных целей можно ограничиться изучением напряженно-деформируемого состояния одного деревянного элемента с вклеенными стальными шайбами.
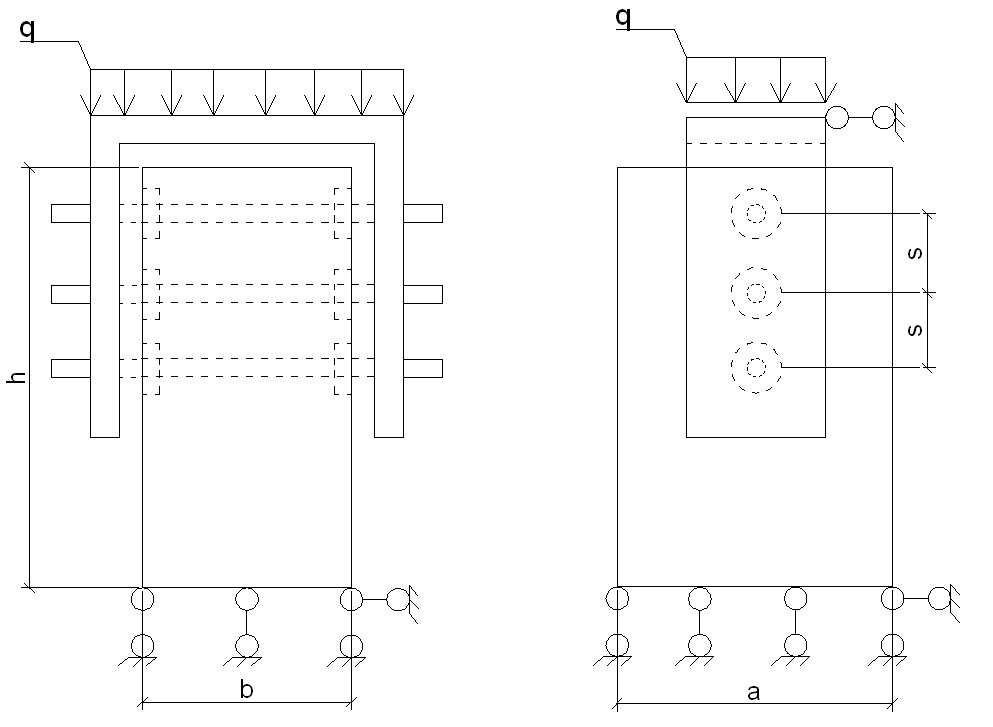
В общем виде расчетная схема многорядных соединений на вклеенных шайбах, принятая для теоретического исследования задачи о напряженно-деформируемом состоянии деревянного элемента показана на рис. 1.
Образец представляет собой соединение из деревянного элемента прямоугольного сечения с вклеенными в него стальными шайбами, нагрузка на образец передается через металлическую раму по средством стяжных болтов, сначала на в клееные шайбы, а потом на деревянный образец.
Шайбы монолитно вклеены в деревянный элемент и поэтому до определенного момента нагружения образца работает совместно с древесиной, т. е. по всему контуру шайбы могут возникать как растягивающие так и сжимающие напряжения. В этом случае имеем дело с одной постановкой задачи, когда связь шайб с древесиной двухсторонняя (способность воспринимать напряжения сжатия и растяжения).
Рис. 1. Расчетная схема многорядного соединения на вклеенных шайбах
При определенном уровне нагружения растянутые связи между шайбами и древесиной теряют прочность (шайба получила сдвиг), тогда совместность работы шайб с древесиной обеспечивается только сжимающими контактными напряжениями. Это другая постановка задачи которая в данной статье не рассматривается.
Образец, работающий на сжатие (растяжение) под воздействием нагрузки, оказывается в условиях объемного напряженного состояния, которое характеризуется шестикомпонентным вектором напряжений
= |x, y, z, xy, xz,yz|
Для перехода от физической модели к математической принимается расчетная схема показанная на рис.1.
Монолитность соединения модели математически описывалось как связывание соответствующих узлов по всем степеням свободы.
Все расчеты были выполнены в программном комплексе ANSYS [6,7,8] ЛИЦЕНЗИЯ № 32413840 от 21.12.2008 г [9] (предоставленная ООО НПП «Геотек»).
Для моделирования металлической шайбы и деревянного элемента был использован конечный элемент Solid92 [6,26] (рис.2).
Рис.
2. Вид конечного элемента Solid92: а)- конечный элемент Solid92; б)-
выдача усилий в элементе Solid92.
Свойства материала требуются для большинства типов элементов. В зависимости от области применения, свойства могут быть линейными, нелинейными или анизотропными. Анизотропные свойства для материалов задаются в матричном виде либо в местной либо в глобальной системе координат (рис.3).
Теоретические исследования напряженно-деформированного состояния соединения по расчетной схеме (рис.1) проводились методом конечных элементов (МКЭ). Степень точности решения задачи, как известно, зависит от величины размеров разбивочных элементов МКЭ [7]. При этом от этого существенно зависит и громоздкость вычислительных операций, поскольку с увеличением количества конечных элементов существенно возрастает количество неизвестных. Для расчетов принято разбивочная сетка МКЭ, изображенная на рис.3.
Рис.3.
Разбивка элемента на сетку МКЭ: а) металлической обоймы с болтами;
б) деревянного элемента.
Параметры образцов, подвергаемых теоретическому расчету, назначались исходя из поставленных целей и приведены в табл. 1.
Таблица 1
|
Диаметр |
S, шаг, мм |
H, высота, м |
B, толщина, мм |
A, ширина, мм |
T, толщина шайб, мм |
||||
|
D-60 |
120 |
180 |
- |
470 |
650 |
- |
120 |
200 |
10 |
|
D-80 |
120 |
160 |
240 |
470 |
590 |
830 |
120 |
200 |
10 |
|
D-100 |
120 |
200 |
300 |
470 |
710 |
1010 |
120 |
200 |
10 |
Расчет производился при действии на образец силы равной P= 50000 Н,(391000000 Па.) на верхнею площадку металлической обоймы согласно рис..1.
Так как в расчете используется два материала — металл, древесина, то в дальнейшем будут приниматься характеристики:
металла Ех=210 ГПа, μ=0,3
древесины Ех=16000 МПа, μyx =0,5; Еу=1000 МПа, μzy =0,2; Еz=500 МПа, μzx=0,02; Gxy=1180 МПа, Gyz=690 МПА, Gхz=670 МПа (согласно исследований Ашкенази [10]), свойства древесины задавались в местной системе координат (рис.1).
Кроме того, результаты расчета образцов позволяют определить безопасные предельно допустимые конструктивные параметры шаг расстановки шайб вдоль и поперек образца (S1,S2), а также минимальные размеры образца axbxc при различных Dш и t.
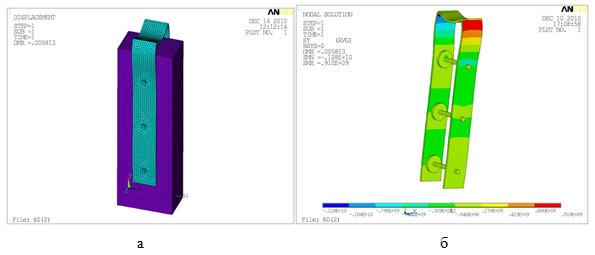
Результаты расчетов по программе Ansys при данных, описанных выше, приведены в виде изополей распределения напряжений.
Рис. 4. Деформаций образца; а) общий вид; б) металлическая обойма
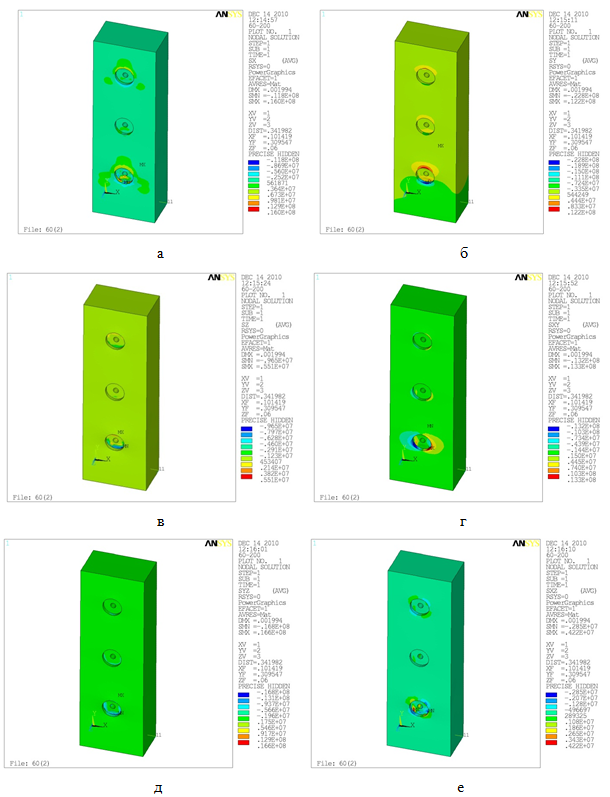
Рис.5. Деформаций образца; а-напряжений x; б- напряжений y;в- напряженийz; г-напряжений τxy д-напряжений τxz;е-напряжений τyz
Как видно из изополей, напряжения распределяются неравномерно и для детального изучения данного распределения необходим боле детальный анализ полученных данных. Данный анализ будет предложен в следующих статьях.
Литература:
Арискин М. В., Вдовин В. М. Соединения на вклеенных стальных шайбах / М. В. Арискин, В. М. Вдовин// Эффективные строительные конструкции: Теория и практика: сборник статей III Международной научно-технической конференции. Пенза: ПГУАС, Общество «ЗНАНИЕ» России, Приволжский дом знаний, 2004. С. 175–177.
Арискин М. В. Экспериментальные исследования соединений на вклеенных шайбах / М. В. Арискин, В. М. Вдовин // Студенческая наука — интеллектуальный потенциал ХХI века: сборник рефератов докладов научно-технической конференции. Пенза: ПГУАС, 2005. С. 35.
Арискин М. В., Вдовин В. М. Кравцов С. Ю. Экспериментальные исследования соединений на вклеенных стальных шайбах / М. В. Арискин, В. М. Вдовин, // Эффективные строительные конструкции: Теория и практика: сборник статей IV Международной научно-технической конференции. Пенза: ПГУАС, Общество «ЗНАНИЕ» России, Приволжский дом знаний, 2005. С. 147–152.
Арискин М. В., Вдовин В. М., С. Ю. Кравцов. К оценке работы несущей способности соединений на вклеенных шайбах / М. В. Арискин, В. М. Вдовин, С. Ю. Кравцов // Эффективные строительные конструкции: Теория и практика: сборник статей V Международной научно-технической конференции. Пенза: ПГУАС, Общество «ЗНАНИЕ» России, Приволжский дом знаний, 2006. С. 18–23
Арискин М. В., Вдовин В. М., Кравцов С. Ю. Клееметаллические соединения в несущих деревянных конструкциях / М. В. Арискин, В. М. Вдовин, С. Ю. Кравцов // Региональная архитектура и строительство. 2007. № 1 (2). С. 18–23
Агапов В. П. Метод конечных элементов в статике, динамике и устойчивости конструкций. Учебное пособие. М., издательство АВС, 2004г.
Чигарев А. В., Кравчук А. С. ANSYS для инженеров: справочное пособие. М., Машиностроение-I, 2004 г.
Басов К. А. ANSYS для конструкторов. Издательство «ДМК-пресс», М.,2009г.
Лицензия [Электронный ресурс]: [сайт]. [2012]. Url:http://www.http://www.npp-geotek.ru/documents/licenses/licensansys/ (дата обращения 06.09.2012)
Ашкенази Е. К., Ганов Э. В. Анизотропия конструкционных материалов. Справочни., Ленинградское отделения издательства «машиностроение»,1980г.