Formal Models of Assessment of Quality of Administrative Education

The Competitiveness of Administrative Education depending on the sphere of research is defined by several aspects:

• set of quality educational programs, baccalaureate, master, various programs of professional development;

• number of carriers of management education (developers of educational programs, professors);

• the system of educational institutes in region/country.

Various spheres of research, but the task mathematically it can be described by one logic. Here it is:

There is a complex of objects, each of which is characterized by a set of attributes:

X = (x₁, x₂, …, x_n) (1)

In the first case we’ll consider following attributes: a lowest passing score, number of professors, number of chairs.

In the second case X vector is presented by attributes: number of winners of the Olympiads, number of graduate students, and number of programs of additional education.

In the 3^rd case we use following attributes: a share of means on scientifically — research works, number of the published textbooks, number of scientific publications.

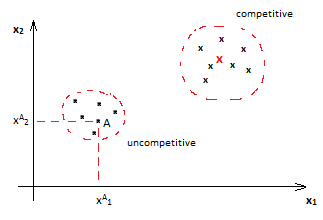
Vector (1) defines so-called feature space of research in which some objects presented by dots, pertains (belong) to the class “competitive”. Some of these objects are not competitive. Pic.1

Pic. 1

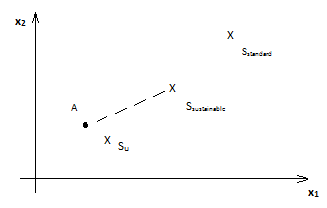
Division into two classes is conditionally. Task originator may define more classes, for example three classes: leading educational institutes (competitiveness which is the reference), steadily (sustainably) developing educational institutes and uncompetitive. Pic.2

Pic. 2

New problems arise:

• Creating set of attributes;

• Defining set and location of classes in selected feature space;

• Identification of location of studied object;

• Making decision on increase measures of CAE.

The first problem may be solved with the experts’ information with additional mathematical processing which will increase reliability of this information (experts may be engaged, unqualified, nay have different opinions).

The solution of second problem — is the result of representative observation and statistical processing of monitoring of studied objects. As a result we have standards of the allocated classes. Pic.2: S_n, S_y, S_s.

The third problem may be solved by direct measurement of established indicators (attributes).

Management is consists of transformation of object’s current condition into desired. For example if the object presented as point A (is in the class of uncompetitive) and desired condition — sustainable development of AE (standard S_y) it have to make a way AS_y based on following criteria: minimum time with maximum costs or another combined requirement.

Following additional mathematical problems are arises at a solution of a task:

• How to estimate adequacy of the model?

• How to provide a representativeness of data?

• What is the distance between points (objects)?

• How to expect optimal movement trajectory from current to desirable condition?

All these questions will have answers in my future research.

Reference:

1. Гольбан Е. В., Лябах Н. Н. (младший). Параметрическая идентификация мер близости признаковых пространств // Изв. Вузов. Сев. — Кавк. Регион. Техн. Науки. 1997. № 2. С. 37–39.