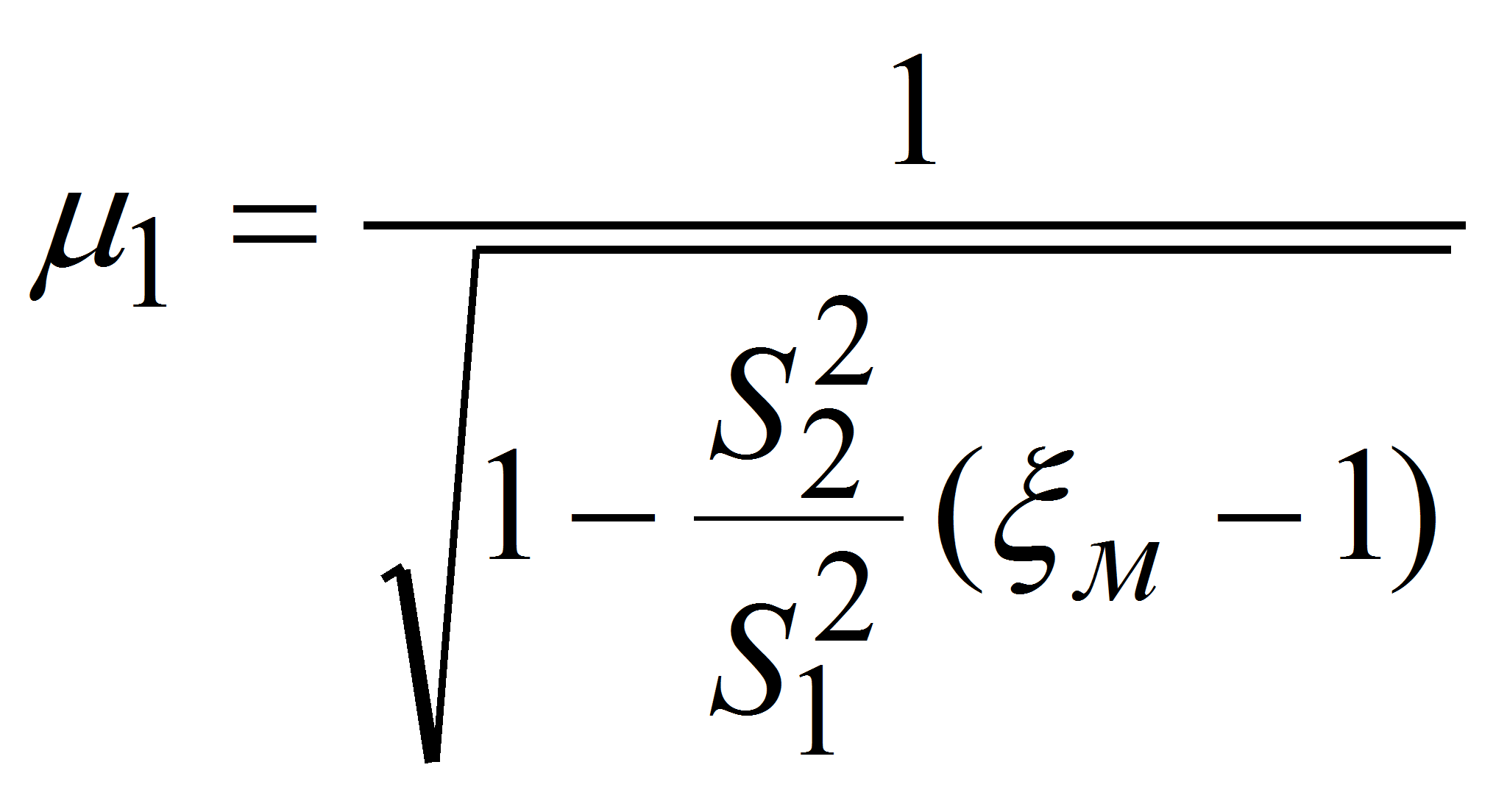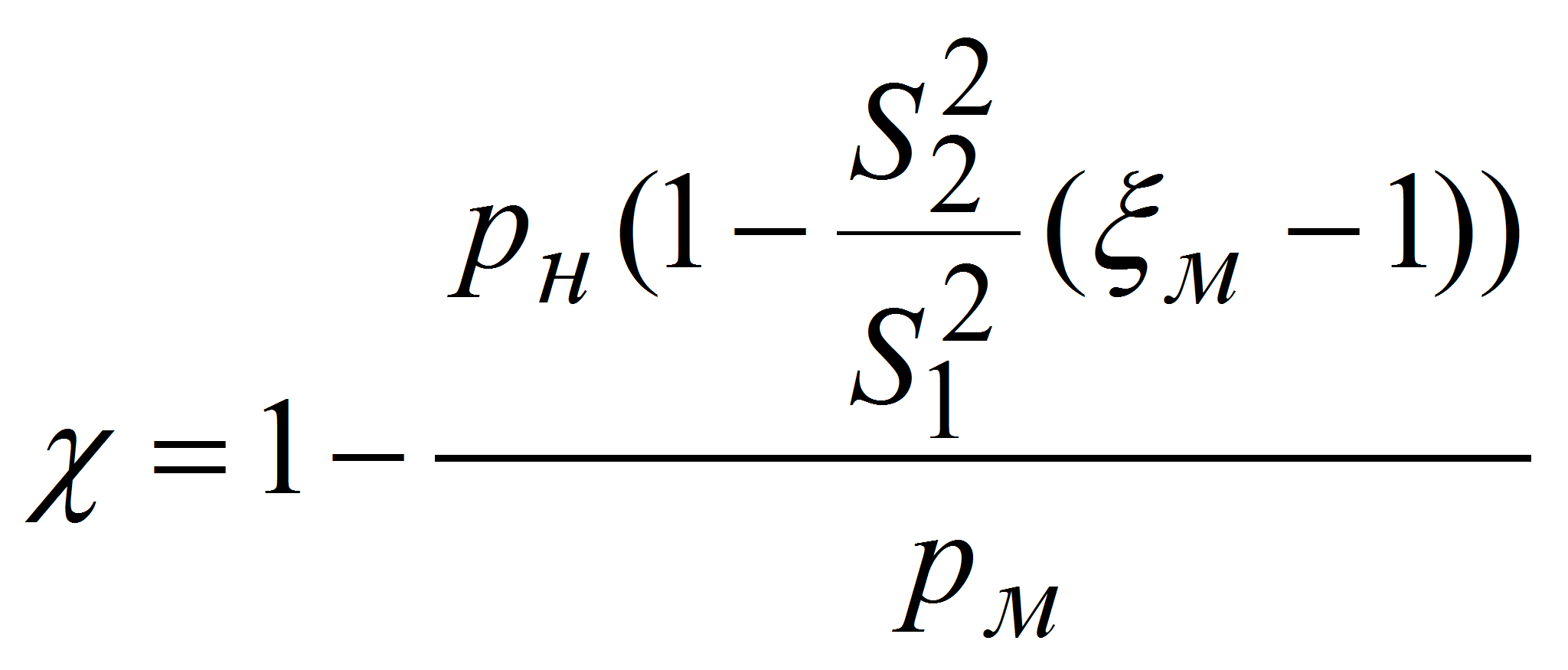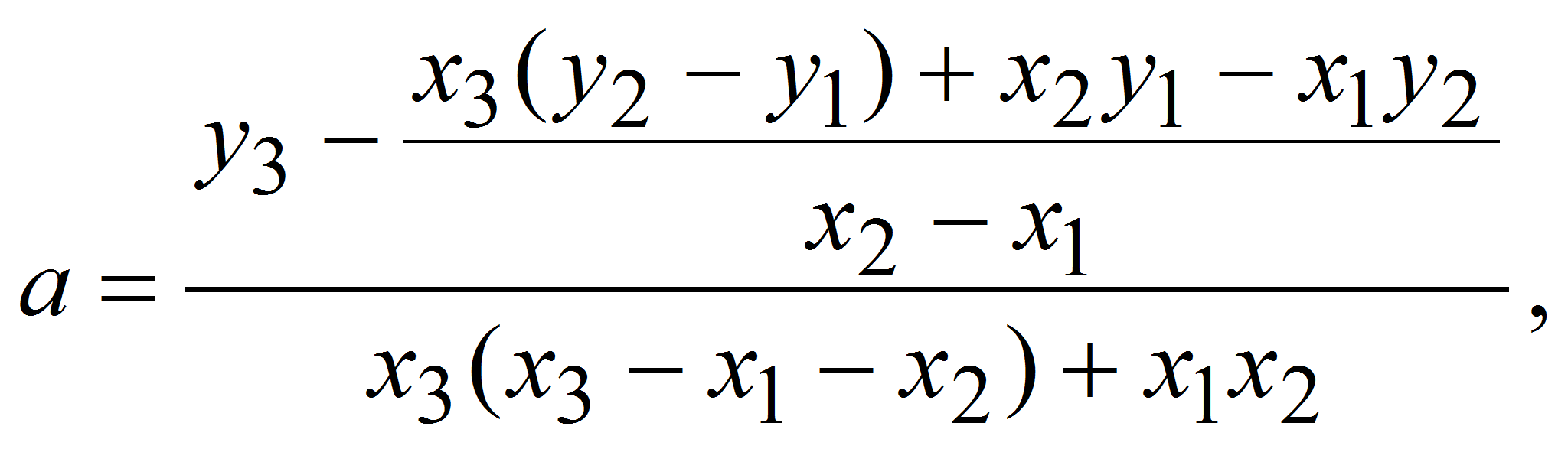Свойства кавитации для разрушения сплошности – диспергирования потоков взаимнонерастворимых веществ в последнее время начали широко использовать для интенсификации некоторых технологических процессов [2]. В научно-исследовательской лаборатории гидродинамики Винницкого НТУ разработано оборудование для приготовления битумных эмульсий, принцип работы которого базируется на создании кавитации [1]. Сопутствующие гидродинамические факторы кавитации создают условия для эмульгирования битума в водном растворе поверхностно-активных веществ [2].
Основным параметром характеризующим процесс кавитации является число кавитации [2], физический смысл которого заключается в соотношении давления, приводящего к схлопыванию кавитационной каверны, к давлению, которое приводит к её образованию и росту:
где р3
– абсолютное давление, Па;
![]() – давление насыщенного пара, Па;
ρ –
плотность вещества, кг/м3;
υ2
– скорость потока жидкости на выходе с самого узкого участка
кавитационного диспергатора, м/с.
– давление насыщенного пара, Па;
ρ –
плотность вещества, кг/м3;
υ2
– скорость потока жидкости на выходе с самого узкого участка
кавитационного диспергатора, м/с.
Целью теоретического исследования рабочего процесса эмульгирования битума с помощью кавитационного диспергатора предложенной конструкции при приготовлении строительной продукции – битумной эмульсии, является: исследование условий возникновения и развития кавитации в кавитационном диспергаторе, разработка модели динамики рабочего процесса эмульгирования битума, выбор обобщенных функциональных зависимостей позволяющих осуществлять выбор рациональных режимов и конструктивных параметров узла эмульгирования, анализ с помощью численного экспериментирования влияния параметров и характеристик установки для приготовления битумной эмульсии на характеристику полученной продукции – битумную эмульсию.
При разработке математической модели рабочего процесса приготовления битумной эмульсии с помощью кавитационного диспергатора предложенной конструкции были приняты следующие допущения: процесс адиабатный; вследствие незначительного, по сравнению с битумом и водой количества соляной кислоты и эмульгатора, их влияние на реологические свойства смеси не учитываются; сжимаемость рабочей жидкости не учитываем; давление насыщенного пара для компонентов, а также плотность каждого из компонентов этой смеси зависят от физико-механических свойств жидкости и от температуры и принимаются в соответствии с рекомендациями [3].
Процесс эмульгирования битума в водном растворе составляющих компонентов эмульсии в предложенной установке для приготовления битумных эмульсий происходит следующим образом [1]. После равномерного распределения составляющих компонентов в потоке сырья, которое происходит в статическом смесителе, сырье поступает в конфузорную часть 1 кавитационного диспергатора (рис. 1), где происходит постепенное сужение потока и, как следствие, увеличивается скорость движения потока, а значит давление в этом сечении также постепенно уменьшается. Далее поток поступает в диффузорную часть 2 кавитационного диспергатора, где конусообразный рабочий орган 3 кавитатора образует зазор между внутренней поверхностью диффузорной части 2 и наружной поверхностью рабочего органа диспергатора 3, регулирование которого обеспечивает дальнейшее падение давления до некоторого критического значения (до давления насыщенного пара для данной жидкости). Обрабатываемая жидкость попадает в зону критического давления, происходит холодное кипение – образование парогазовых пузырьков (кавитация), которые двигаются дальше и при попадании в зону повышенного давления (за узлом эмульгирование) интенсивно схлопывают, разрушая при этом сплошность потока, т.е. осуществляется диспергирование битума в водном растворе ПАВ.
Рис. 1. Схема получения битумной эмульсии в кавитационном диспергаторе предложенной конструкции
Для определения скорости прохождения потока жидкости через зазор, образованный внутренней поверхностью конфузорной части и поверхностью рабочего органа кавитационного диспергатора, запишем уравнение Бернулли для сечений 1-1 и 2-2:
где
![]() –
геометрический напор в сечениях 1-1
и 2-2, м;
–
геометрический напор в сечениях 1-1
и 2-2, м;
![]() –
абсолютное давление в сечениях 1-1
и 2-2, Па;
–
абсолютное давление в сечениях 1-1
и 2-2, Па;
![]() –
удельный вес, Н/м3;
–
удельный вес, Н/м3;
![]() – скорость движения
потока жидкости в
сечениях 1-1
и 2-2,
м/с;
– скорость движения
потока жидкости в
сечениях 1-1
и 2-2,
м/с;
![]() – суммарные
потери давления на участке
между рассматриваемыми
сечениями, м.
– суммарные
потери давления на участке
между рассматриваемыми
сечениями, м.
Уравнение потерь для сечений 1-1 и 2-2:
![]()
где
![]() – площадь поперечного сечения проходных отверстий диспергатора
1-1 и 2-2, м2.
– площадь поперечного сечения проходных отверстий диспергатора
1-1 и 2-2, м2.
Пренебрегая потерями давления по длине, вследствие их малости, потери на местных сопротивлениях рассчитываем по формуле Дарси-Вейсбаха [5]:
где
![]() – коэффициент местного сопротивления.
– коэффициент местного сопротивления.
Следовательно, скорость движения потока сырья через сечение 2-2:
где
![]() – избыточное давление,
Па;
– избыточное давление,
Па;
![]() – коэффициент, который
определяем по формуле:
– коэффициент, который
определяем по формуле:
При рассмотрении сечения 3-3 получим значение абсолютного давления, при котором происходит схлопывание кавитационных пузырьков:
где
![]() – скорость движения
потока сырья в
сечении 3-3,
м/с.
– скорость движения
потока сырья в
сечении 3-3,
м/с.
Поскольку расстояние между сечениями
2-2 и
3-3 мало,
то предположим, что
![]() .
Подставив в
(1) уравнения
(5) и (7),
получим число кавитации:
.
Подставив в
(1) уравнения
(5) и (7),
получим число кавитации:
После подстановки в уравнение (8) выражения (6), окончательно получим:
Из анализа уравнения (9) видно, что с увеличением давления в системе число кавитации увеличивается. Кроме того, происходит увеличение числа кавитации также с увеличением площади зазора между рабочим органом и внутренней поверхностью диффузорной части диспергатора.
Был рассмотрен реальный
процесс приготовления
битумной эмульсии в
кавитационном диспергаторе
при следующие параметрах:
давление насыщенного пара
низкокипящих компонента
(воды) при температуре потока
сырья Т=900
[3],
![]() =
70927,5 Па; площадь поперечного
сечения входного
патрубка конфузорной
части диспергатора,
=
70927,5 Па; площадь поперечного
сечения входного
патрубка конфузорной
части диспергатора,
![]() =0,000804
м2; плотность
битума при нагревании
приближается к плотности
водного раствора
эмульгатора, поэтому на
основании проведенных опытов установлено, что
плотность механической
смеси входящих компонентов
сырья может быть принята
равной
=0,000804
м2; плотность
битума при нагревании
приближается к плотности
водного раствора
эмульгатора, поэтому на
основании проведенных опытов установлено, что
плотность механической
смеси входящих компонентов
сырья может быть принята
равной
![]() ≈
1000 кг/м3;
согласно [5] усредненное значение коэффициента местного сопротивления
между сечениями
1-1 и
3-3 было принято
≈
1000 кг/м3;
согласно [5] усредненное значение коэффициента местного сопротивления
между сечениями
1-1 и
3-3 было принято
![]() =1,44.
=1,44.
На основании вышепринятых параметров можно построить
зависимость числа кавитации
![]() от давления в системе
от давления в системе
![]() (рис. 2) и числа кавитации
(рис. 2) и числа кавитации
![]() от площади зазора между рабочим органом и внутренней поверхностью
дифузорной части кавитационного диспергатора
от площади зазора между рабочим органом и внутренней поверхностью
дифузорной части кавитационного диспергатора
![]() (рис. 3).
(рис. 3).
Рис. 2. Зависимость числа кавитации от давления на входе в диспергатор
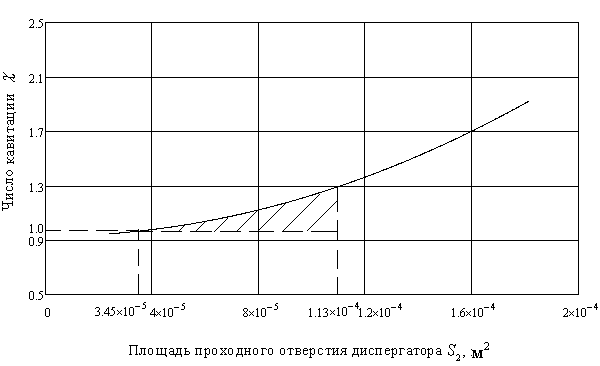
Рис. 3. Зависимость числа кавитации от площади проходного отверстия диспергатора
Увеличение числа кавитации при увеличении давления на входе в узел диспергирования и увеличение зазора между рабочим органом и внутренней поверхностью диффузорной части диспергатора объясняется ростом скорости истечения сырья через сечение 2-2.
Найдем скорость движения сырья через сечение 1-1:
Как было отмечено в [7] «... Качество эмульсии, при прочих равных условиях, определяется ее дисперсностью, т.е. размером дисперсной фазы. Высокая дисперсность битума в дорожных эмульсиях и пастах обусловливает их устойчивость и существенно влияет на основные технологические свойства – вязкость, скорость распада, однородность, толщину пленки вяжущего и сцепление с минеральными материалами... ».
Как показал анализ предыдущих известных исследований, прямой зависимости между числом кавитации и дисперсностью полученной эмульсии нет. Предварительные экспериментальные исследования показали, что кривая зависимости между дисперсностью и числом кавитации имеет вид параболы, ограниченной граничными условиями. Следовательно, зависимость между числом кавитации и размером частиц битума можно приближенно представить квадратным уравнением:
где а, b, c – экспериментальные коэффициенты; х – число кавитации.
Подставим (10) в (13):
Согласно [8], коэффициенты а, b, а также свободный член с зависимости (14), которые находятся экспериментально, можно определить по формулам:
где
![]() – абсциссы трех любых точек, находящихся на экспериментальной
кривой;
– абсциссы трех любых точек, находящихся на экспериментальной
кривой;
![]() – соответственно ординаты этих точек.
– соответственно ординаты этих точек.
Например, согласно экспериментальных данных, зависимость дисперсности от площади проходного отверстия диспергатора при постоянном давлении р = 0,9 МПа и количестве битума в эмульсии п=60% приведена на рис.4.
Рис. 4. Зависимость диаметра частичек битума от площади проходного отверстия диспергатора при р = 0,9МПа та п= 60%.
В данном случае уравнение (14) принимает вид:
Сводная таблица 1 иллюстрирует значение старшего а, второго b коэффициентов и значение свободного члена c в зависимости от параметров обработки компонентов эмульсии.
Таблица 1
Уточняющие коэффициенты
математической модели процесса
эмульгирования
битума в
предложенной
кавитационной
установке
|
Параметры диспергирования |
Коэффициенты |
Свободный член, с |
|||
|
Площадь проходного отверстия диспергатора, S, мм2 |
Количество битума в эмульсии, n, % |
Давление на входе в диспергатор Р, МПа |
|||
|
старший, а |
второй, b |
||||
|
var |
40 |
0,9 |
6,491444 |
-11,95647 |
5,505604 |
|
var |
60 |
0,9 |
5,2425 |
-9,65553 |
4,445847 |
|
var |
40 |
1,1 |
23,666031 |
-44,280461 |
20,712804 |
|
var |
60 |
1,1 |
-0,000663 |
0,01434 |
-0,012833 |
|
var |
50 |
1 |
0,12056 |
-0,070093 |
0,010189 |
|
73,5 |
50 |
var |
-0,000417 |
0,0006707 |
-0,00025488 |
На основании
принятых допущений
исследована кинетика
эмульгирования битума
в кавитационном
диспергаторе и
выполнено математическое моделирование
процесса кавитационного
диспергирования составляющих
битумной эмульсии, которое
отражает конструктивные
особенности предлагаемого
узла диспергирования.
Установлена аналитическая
зависимость, которая
связывает между собой конструктивные
и технологические параметры
приготовления эмульсии:
площадь проходного отверстия
кавитационного диспергатора
![]() ,
давление на входе в
диспергатор рм
и характеристику полученной
битумной эмульсии
– размер частички битума в эмульсии
,
давление на входе в
диспергатор рм
и характеристику полученной
битумной эмульсии
– размер частички битума в эмульсии
![]() .
На основе предварительно
проведенных экспериментальных исследований
установлены уточняющие
коэффициенты для составления
математической модели процесса
эмульгирования битума
в предложенной
кавитационной установке.
.
На основе предварительно
проведенных экспериментальных исследований
установлены уточняющие
коэффициенты для составления
математической модели процесса
эмульгирования битума
в предложенной
кавитационной установке.
Литература:
Пат. 37338 Україна, МПК8 E01C 19/00 Установка для приготування бітумних емульсій / Борисенко А. А., Бауман К. В., Коц І. В.– № u200807653; заявл. 04.06.08; опубл. 25.11.08, Бюл. № 22.
Кулагин В. А. Методы и средства технологической обработки многокомпонентных сред с использованием эффектов кавитации: Дис.... доктора техн. наук : 01.04.11, 01.02.05 / Кулагин В. А. - Красноярск, 2004. - 299 c.
Ривкин С. Л. Термодинамические сойства воды и водяного пара: Справочник. Рек. Гос. Службой стандартних справочных данных – 2-е узд., перераб. и доп. / Ривкин С. Л., Александров А. А. – М.: Энергоатомиздат, 1984. - 80 с.
Калицун В. И. Основи гидравлики и аэродинамики / Калицун В. И., Дроздов Е. В. – М.: Сройиздат, 1980. – 247 с.
Идельчик И. Е. Справочник по гидравлическим сопротивлениям/ Под ред. М. О. Штейнберга. — 3-е изд., перераб. и доп.— М.: Машиностроение, 1992. — 672 с.
Радовський Б. С. Дисперсність емульсії при гідродинамічному проточно-кавітаційному способі її отримання / Радовський Б. С., Мозговий В. В., Гамеляк І. П., [та ін.] // Автомоб. дороги і дор. буд-во.- 1997.- Вип. 54.- С. 115-119.
Акопян А. А. Геометрические свойства кривых второго порядка. / Акопян А. А., Заславский А. В. – М.: МЦНМО, 2007. –– 136 с. - ISBN 978-5-94057-300-5.