Основой государственной кадастровой оценки земель садоводческих, огороднических и дачных объединений является установление уравнения связи между рыночной стоимостью земельных участков и факторами кластеризации, а также проверка достаточности связи в уравнении.
Таким образом, в результате кадастровой оценки, строится модель и определяется некоторая функция стоимости от параметров земельного участка, приближенно описывающая рыночную ситуацию. В этом, собственно и выражается суть массовой оценки недвижимости.
Кадастровая стоимость садоводств Ленинградской области является сложной составляющей, которая находится под влиянием большого числа трудно учитываемых факторов, поэтому математическое моделирование не может дать исчерпывающую характеристику кадастровой стоимости. Следовательно, любая математическая модель является приближенным отражением реальной кадастровой стоимости на данной территории и для данной территории можно построить несколько математических моделей различной степени сложности [5].
Рассмотрим построение аддитивной и мультипликативной моделей определения кадастровой стоимости на примере садоводств Ленинградской области.
Среди трех методов рыночной оценки недвижимости – затратного, доходного и метода сравнения продаж – для массовой оценки достаточно ориентироваться только на последний из них. Имеется достаточно много рыночной информации о ценах предложений на земельные участки. Поэтому нет необходимости ориентироваться на косвенные методы определения их рыночной стоимости (затратный и доходный), которые в условиях несбалансированного рынка могут давать неадекватные представления о стоимости земельных участков.
Методика массовой оценки, базирующаяся на методе сравнения продаж и определяющая рыночную стоимость земельного участка в зависимости от его параметров, может создаваться разными путями. Один из таких подходов, который используется в настоящее время, базируется на использовании статистического анализа. Основным и традиционным статистическим методом, имеющимся в распоряжении оценщика, для калибровки моделей сравнения продаж является множественный регрессионный анализ. Множественный регрессионный анализ – это статистический способ определения неизвестных данных на основе известной и доступной информации. В массовой оценке неизвестными данными являются значения рыночной стоимости. К известным данным относятся цены предложений и характеристики объектов недвижимости. Современные статистические пакеты позволяют строить модели как линейной, так и нелинейной регрессии. В качестве уравнений регрессии, например, при спецификации парных моделей привлекаются следующие функции: линейная, степенная, показательная, гиперболическая, полиномиальная. Уравнения регрессии в нелинейных моделях могут быть нелинейными как по переменным, так и по параметрам. При оценке эконометрических моделей с нелинейными уравнениями регрессии возникают некоторые сложности, которые отсутствуют при оценке эконометрических моделей с линейными уравнениями [1]. Методы построения линейных моделей существенно проще и надежней. Они предъявляют менее жесткие требования к количеству исходной информации и лучше приспособлены для учета возможных зависимостей между параметрами [2]. При обработке собранных данных в Ленинградской области использовалась линейная модель определения расчетной рыночной стоимости земель садоводств [3]. Поэтому будем ориентироваться на построение модели линейной регрессии.
Основным видом модели, к которой применяется множественный регрессионный анализ, является аддитивная модель. Общая структура аддитивной модели выглядит следующим образом:
где y – зависимая переменная;
x1,x2,…,xp – независимые переменные;
b1,b2,…,bp – коэффициенты(веса) приписываемые в процессе работы алгоритма независимым переменным;
b0 – константа.
Изучим влияние факторов, определяющих цену земельных участков в садоводческих некоммерческих объединениях, в аддитивной модели, и проверим ошибку полученного уравнения в “точках съема информации”.
Множественный регрессионный анализ также предполагает, что зависимые переменные не коррелируют между собой. Ситуация, когда это условие нарушается – мультиколлинеарность – довольно частое явление в массовой оценке. Простой процедурой уменьшения мультиколлинеарности является исключение избыточных переменных [2].
Построим уравнение множественной регрессии, характеризующее зависимость цены от всех факторов в линейной форме методом включения, оценим адекватность полученной модели.
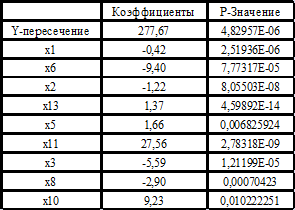
Построение модели методом включения - это пошаговый отбор переменных. В результате получаем отчет регрессии по 9-ти переменным (табл.1).
Таблица 1
Фрагмент отчета регрессии по 9-ти переменным
В результате получаем расчетное уравнение:
которое адекватно описывает зависимость стоимости земельного участка от влияющих на него факторов, и может быть использовано для анализа и прогноза. Все коэффициенты при неизвестных в нем значимы и R2 -коэффициент детерминации равен 0.88.
Итак,
увеличение расстояния до Санкт-Петербурга на 1 км приводит к снижению стоимости сотки земельного участка на 420 рублей;
увеличение расстояния до районного центра на 1 км приводит к снижению стоимости сотки земельного участка на 1220 рублей;
увеличение расстояния до ближайшего населенного пункта на 1 км приводит к снижению стоимости сотки земельного участка на 5590 рублей;
увеличение число рейсов в день на 1 единицу приводит к увеличению стоимости сотки земельного участка на 1660 рублей;
увеличение расстояния до водоема на 1 км приводит к снижению стоимости сотки земельного участка на 9390 рублей;
увеличение уровня преступности приводит к снижению стоимости сотки земельного участка на 2900 рублей;
расположение земельного участка на территории с почвой дерново-карбонатного типа приводит к увеличению стоимости сотки земельного участка на 9230 рублей;
расположение земельного участка на территории с почвой дерново-подзолистого типа почв приводит к увеличению стоимости сотки земельного участка на 27560 рублей;
увеличение расстояния до источника загрязнения химическими веществами на 1 км приводит к увеличению стоимости сотки земельного участка на 1370 рублей.
Определим ошибку полученного уравнения в “точках съема информации”, т.е. вычислим среднюю ошибку аппроксимации.
Средняя ошибка аппроксимации для данного уравнения равна 12,5%. О хорошем качестве полученной модели можно говорить при ошибке аппроксимации от 10-12%. В нашем случае в отдельных “точках съема информации” фактическое значение результативного признака отличается от теоретического, рассчитанного по уравнению регрессии до 35%. Что является не допустимым для проведения качественной кадастровой оценки садоводческих некоммерческих объединений.
Так полученная аддитивная модель при своих достоинствах имеет и ряд недостатков. Так, например, характерной особенностью данной модели является также возможность получения в какой-то точке исследования отрицательного результата, т.е. при отдельных значениях ценообразующих факторов (например, удаленность от Санкт-Петербурга) цена за 1 сотку, теоретически, может иметь отрицательное значение.
Как видно из сказанного выше, использование аддитивной модели связано с целым рядом ограничивающих условий. А мультипликативная модель частично свободна от них.
Мультипликативная модель имеет следующий вид:
Изучим влияние факторов, определяющих цену земельных участков в садоводческих некоммерческих объединениях, в мультипликативной модели, и проверим ошибку полученного уравнения в “точках съема информации”. В результате получаем отчет регрессии по 6-ти переменным (табл.2).
Таблица 2
Фрагмент отчета регрессии по 6-ти переменным
-
Коэффициенты
P-значение
Y-пересечение
4,67
2,03E-26
x1
-0,38
3,85E-07
x2
-0,14
0,016256
x3
-0,09
0,000734
x10
1,49
1,4E-19
x11
1,49
1,33E-17
x12
1,56
3,88E-18
В результате получаем расчетное уравнение:
которое адекватно описывает зависимость стоимости земельного участка от влияющих на него факторов, и может быть использовано для анализа и прогноза. Все коэффициенты при неизвестных в нем значимы и R2 -коэффициент детерминации равен 0.81.
Итак,
увеличение расстояния до Санкт-Петербурга на 1 км приводит к снижению стоимости сотки земельного участка на 380 рублей;
увеличение расстояния до районного центра на 1 км приводит к снижению стоимости сотки земельного участка на 140 рублей;
увеличение расстояния до ближайшего населенного пункта на 1 км приводит к снижению стоимости сотки земельного участка на 90 рублей;
расположение земельного участка на территории с почвой дерново-карбонатного типа приводит увеличению стоимости сотки земельного участка на 1490 рублей;
расположение земельного участка на территории с почвой дерново-подзолистого типа приводит увеличению стоимости сотки земельного участка на 1490 рублей;
расположение земельного участка на территории с почвой дерново-карбонатного типа приводит увеличению стоимости сотки земельного участка на 1560 рублей.
Определим ошибку полученного уравнения в “точках съема информации”, т.е. вычислим среднюю ошибку аппроксимации. Средняя ошибка аппроксимации для данного уравнения равна 12,5%. О хорошем качестве полученной модели можно говорить при ошибке аппроксимации от 10-12%. В нашем случае в отдельных “точках съема информации” фактическое значение результативного признака отличается от теоретического, рассчитанного по уравнению регрессии до 35%. Что является не допустимым для проведения качественной кадастровой оценки садоводческих некоммерческих объединений.
В результате построения различных моделей определения кадастровой стоимости земель садоводств Ленинградской области были получены различные уравнения зависимости стоимости от факторов. В результате проверки невозможно определить, какая модель наиболее точно описывает систему. Чаще всего оценивается степень совпадения или сходства фактических данных с теоретическими, вычисленными в ходе решения математической модели. Средняя ошибка аппроксимации для двух уравнений равна 12,5%.
Представленные математические модели отражают зависимость стоимости недвижимости от основных характеристик. Для практической реализации массовой оценки необходимо проведение научных исследований и экспериментальных расчетов.
Таким образом, моделирование объектов оценочной деятельности является актуальным и перспективным направлением проведения исследований. Переход от плановой экономики к рыночной и развитие системы налогообложения требует дальнейшего интенсивного развития моделей и методов оценки, повышения достоверности результатов и проведения оценки объектов на территории Российской Федерации.
Литература:
Бабешко Л.О. Основы эконометрического моделирования: учебное пособие, изд.4-е. - М.: КомКнига, 2010.-432с.
Новиков Б.Д. Рынок и оценка недвижимости в России. - М.:”Экзамен”, 2000. - 512с.
Отчет о работе контрольно-счетной палаты Ленинградской области за 2006 год.
Попова Л.В. Математические методы в оценке: учебное пособие. - М.: Дело и Сервис. - 2011. - 112с.
Поротов Г.С. Математические методы моделирования в геологии: Учебник / Г.С.Поротов. Санкт-Петербургский государственный горный институт (технический университет). СПб, 200. 223 с.