- В докладе
рассматривается методика выявления информационных зависимостей в
программном коде. Уделяется внимание процессу анализа исходного
текста программы, описывается алгоритм построения графа
информационных связей, а также приводится пример, иллюстрирующий
этапы выявления информационных зависимостей. Приводится ряд
направлений, для которых рассматриваемая методика имеет высокую
степень применимости. Одной из таких задач является задача
оптимизации сложности вычислений, при решении которой необходимо
учитывать как все возможные скрытые зависимости состояний по данным,
так и выполнение операций в их логической последовательности.
- Выявление скрытых зависимостей в программном обеспечении является основополагающим этапом проведения верификации программы и позволяет получить полную схему взаимодействия различных функциональных блоков программного обеспечения. Таким образом, построение графа информационных зависимостей программы является одним из возможных подходов решению проблемы распараллеливания вычислений. Кроме того, предложенная методика хорошо применима в области верификации программного обеспечения [1]. Граф информационных зависимостей позволяет учитывать все особенности логической и информационной структуры программы, что является основным аспектом при построении моделей программы [2].
- Введение
- Постоянное повышение
мощности компьютерных систем приводит к тому, что задачи, которые
еще в недалеком прошлом не могли быть решены в реальном масштабе
времени, успешно решаются благодаря использованию параллельных
алгоритмов, реализуемых на многопроцессорных системах, обладающих
высоким быстродействием. Современное программное обеспечение
характеризуется высокой степенью параллелизма протекающих в нём
процессов. Выполняясь одновременно и независимо, между ними возможно
взаимодействие в некоторые моменты времени, т.е. программное
обеспечение является системой, с параллельно функционирующими и
асинхронно взаимодействующими компонентами.
- Бурное развитие многопроцессорных систем и накопленный багаж последовательных алгоритмов делают актуальной задачу распараллеливания существующих императивных алгоритмов. Её решение предлагается разделить на два этапа: анализ исходного кода и синтез параллельной системы. Анализ необходим для выявления скрытого параллелизма в исходной последовательной программе. Прежде всего, сюда включается выявление зависимостей по данным между операторами языка описания алгоритма. На этапе анализа могут собираться сведения о необходимом размещении данных в случае, если используется система с распределенной памятью. Кроме того, возможен сбор сведений о времени выполнения различных участков программы с целью выбора наилучшего варианта распараллеливания системы.
- Методика построения графа информационных связей в программе
- Любое императивное программное обеспечение, в общем случае, представляет собой набор операторов, которые выполняются в строго заданном порядке. Порядок их исполнения определяется алгоритмом работы приложения. Выделим следующие группы алгоритмов:
- Линейные алгоритмы. В коде отсутствуют логические переходы, операторы выполняются последовательно друг за другом;
- Алгоритмы разветвленной структуры. В коде программы присутствуют логические или безусловные переходы. Выполнение того или иного оператора зависит от введенного условия.
- Алгоритм построения
графа информационных зависимостей рассмотрим на примере кода,
написанного на языке Pascal:

- Для построения информационных связей между состояниями программы разработанная методика предполагает выполнение следующих шагов:
- Синтаксический разбор программы. На данном этапе анализируется исходный код программы, выявляются основные синтаксические конструкции. Результатом проведения синтаксического анализа становится синтаксическое дерево программы, расширенное рядом дополнительных показателей. К их числу относятся типы данных, количество дочерних узлов на текущей ветки дерева, уникальный номер функционального блока и его тип.
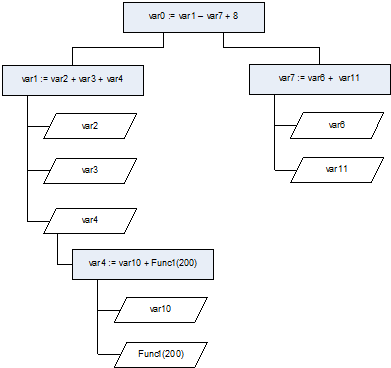
- На втором этапе, используя синтаксическое дерево, выделяются все возможные состояния – изменения связи объектов данных (переменных) с их значениями. Изменение значений является побочным эффектом операции «присваивания», и во многих современных языках программирования сама операция также возвращает некоторый результат (как правило, копию присвоенного значения). На физическом уровне результат операции присвоения состоит в проведении записи и перезаписи ячеек памяти или регистров процессора Для таких распространенных языков программирования, как C, C++, Pascal, Delphi, состояния будем определять наличием в выражении оператора «=» ( С, С++) или «:=» (Pascal, Delphi). В синтаксическом дереве выделяются узлы, имеющие указанные операторы.
Рис.1. Дерево зависимостей состояний от переменных
- Среди выделенных узлов определяют те, которые тем или иным образом зависят друг от друга. Критерием для поиска таких состояний являются участвующие в операции переменные. Другими словами, зависимость состояния от другого состояния выражается в том, в какой части выражения участвует рассматриваемая переменная. Для зависимых состояний, она справа(RValue) от оператора присваивания (записи). Осуществляя поиск вхождений каждой переменной программы в выделенные состояния, можно получить дерево зависимости состояний от переменных (Рис.1). Отдельное место в процедуре поиска зависимостей выделяется для операторов работы с памятью, вызов процедур и функций. Такие операции в скрытом виде имеют возможность модификации переменных, что в свою очередь осложняет процесс построения дерева информационных связей.
- Для каждого узла построенного на этапе 3 дерева осуществляется поиск состояний, в которых переменные участвуют в левой (LValue) части выражения, проводится анализ вызовов процедуру и функций (рассматриваемая подпрограмма оценивается как дискретная, независимая программа). При этом учитываются все найденные ранее взаимосвязи «глобальных» переменных с подпрограммами в анализируемом коде. Совместив дерево зависимостей состояний от переменных и построенного на данном шаге дерева, имеется возможность построить искомое дерево зависимостей состояний от состояний (Рис.2).
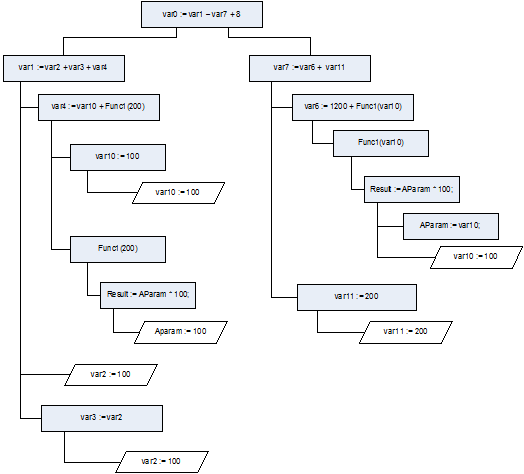 Рис.2.
Дерево зависимостей состояний программы
Рис.2.
Дерево зависимостей состояний программы
-
- В результате анализа строится непосредственно граф зависимостей, вершинами которого являются выделенные состояния программы. Стоит отметить, что для упрощения построения графа, можно использовать таблицу, строками которой являются переменные, а столбцами – состояния. На пересечении строки и столбца ставиться маркер, если переменная участвует в данном состоянии. Используя сформированную таблицу, можно упростить процесс построения будущего графа. Объясняется это тем, что состояния, не имеющие ни одного маркера, не являются значимыми для построения модели программы, т.к. не могут влиять на ход выполнения операций.
- При построении графа информационных зависимостей необходимо учитывать не только связи состояний по данным, но и логическую связь между ними. Две операции программы называются информационно зависимыми, если результат выполнения одной операции используется в качестве аргумента в другой. Очевидно, что если операция B информационно зависит от операции A (то есть, использует какие-то результаты операции A в качестве своих аргументов), то операция B может быть выполнена только по завершении операции A. С другой стороны, если операции A и B не являются информационно зависимыми, то алгоритмом не накладывается никаких ограничений на порядок их выполнения, в частности, они могут быть выполнены одновременно. Таким образом, задача распараллеливания программы сводится к нахождению в ней достаточного количества информационно независимых операций, распределению их между вычислительными устройствами, обеспечению синхронизации и необходимых коммуникаций. Это особенно важно в случаях, когда код написан с использованием ветвящихся алгоритмов. Переходы системы из состояния в состояние в таких программах зависит не только от результата выполнения предшествующей операции, но и логического условия, указанного в том или оном состоянии.
- В общем случае, задача построения графа информационных зависимостей сводится к выявлению в программе всех возможных состояний, а также выяснению зависимостей между ними. При этом важной особенностью таких связей является то, что взаимодействие функциональных блоков системы происходит не только на основании передаваемых между ними данных, но и в строго определенном порядке. Вместе с этим, программа рассматривается как информационная система, имеющая конечное число функциональных модулей, механизм их взаимодействия, а также конечное число состояний.
- Граф информационных зависимостей программы помимо решения задач одного из этапов процесса построения модели программы дает возможность получения различных схем распараллеливания вычислений. Одной из существенных характеристик параллельно выполняющихся частей кода является то, что между ними отсутствует зависимость по данным. Это позволяет говорить о том, что существует как минимум несколько вариантов параллельного исполнения программы. Выбор необходимой схемы обуславливает появление в методики неких оценок, являющимися критериями для выбора оптимального варианта распараллеливания вычислений. Получение адекватных оценок времени выполнения программ или их выделенных фрагментов важно для эффективного распараллеливания, планирования вычислительных процессов и распределения ресурсов масштабируемых систем, а также для оптимизации программ. Довольно часто временные характеристики программы исследуются на инструментальной системе, а затем делается прогноз динамики программы на целевой вычислительной платформе. Как правило, инструментальные средства для такого рода анализа представляют собой сложные программные комплексы, позволяющие выявлять узкие места в работе пользовательских программ и добиваться ускорения их выполнения за счет оптимизации, в том числе и путем структурных преобразований программ. В процессе распараллеливания вычислений необходимо достижение максимального использования имеющихся ресурсов. При этом общее время выполнения исполняемого кода в параллельных обрабатывающих модулях необходимо минимизировать.
- Как было сказано выше, синтез параллельной системы включает выбор схемы распределения данных и вычислений, а также непосредственно генерацию текста параллельной программы с использованием подходящих инструментов. Решение задачи распараллеливания выполнения блоков программы является сложной задачей. При ее разрешении необходимо учитывать как все возможные скрытые зависимости состояний по данным и требование выполнения операций в их логической последовательности, так и оптимальность использования имеющихся в системе ресурсов.
- Среди существующих методов описания и анализа параллельных систем выделяется подход, основанный на использовании сетевых моделей. При построении моделей сложных систем со множеством состояний и переходов обязательным условием остаётся учёт таких её свойств как: случайность времени выполнения операции, возможность одновременного выполнения групп операторов, а также стохастический характер переходов. Для анализа и решения задач моделирования процесса функционирования динамических систем предлагается использовать сети Петри - Маркова [2].
- Сетью Петри-Маркова называется структурно-параметрическая модель, заданная парой
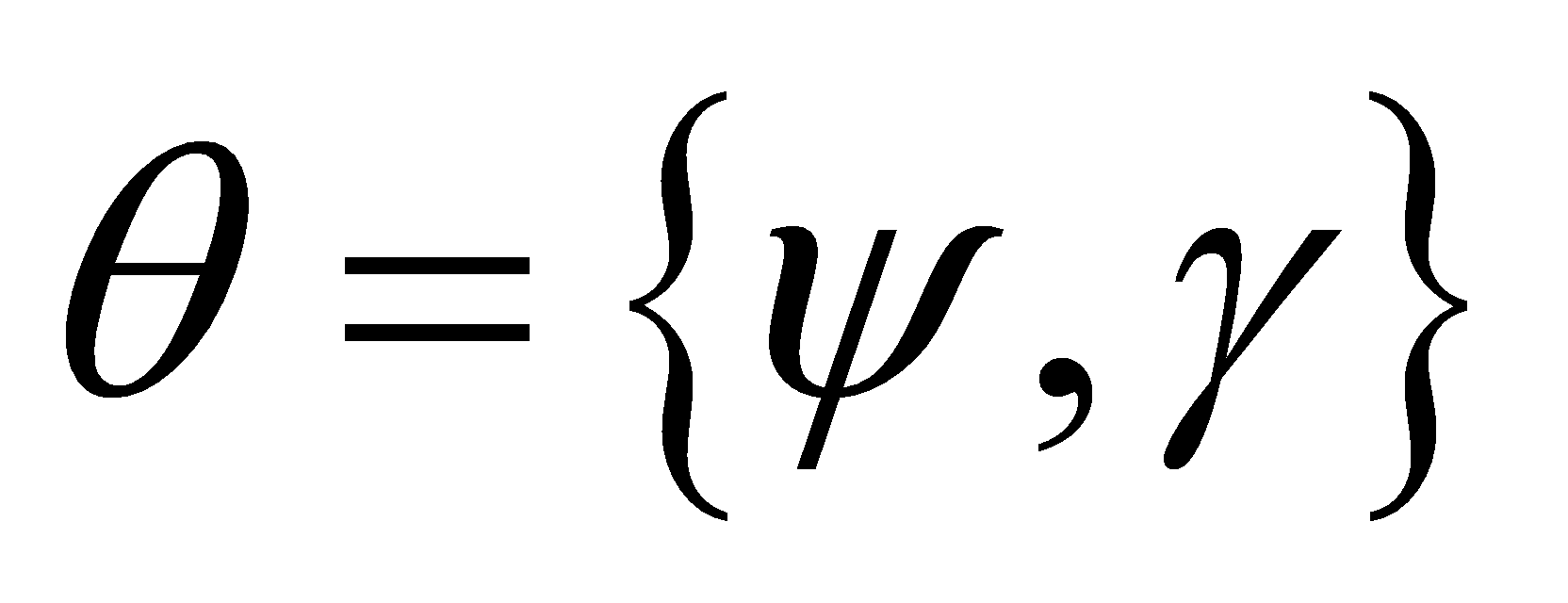 ,
,- где
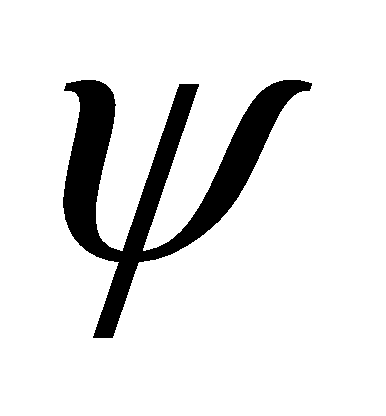 - множество резидентных свойств (структурно-параметрические
характеристики);
- множество резидентных свойств (структурно-параметрические
характеристики);
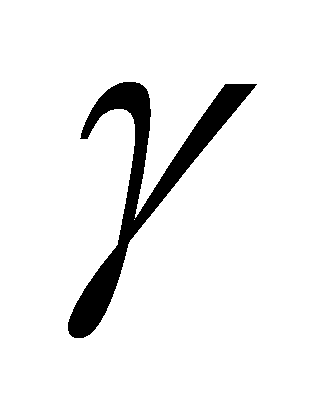 - множество вариационных свойств (характеристики состояния).
- множество вариационных свойств (характеристики состояния).- Резидентные свойства СПМ, в свою очередь, задаются парой
 ,
,- где
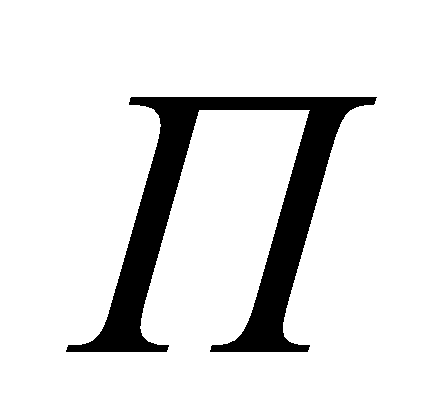 - сеть Петри [4];
- сеть Петри [4];
 - случайный процесс.
- случайный процесс.- Сеть Петри
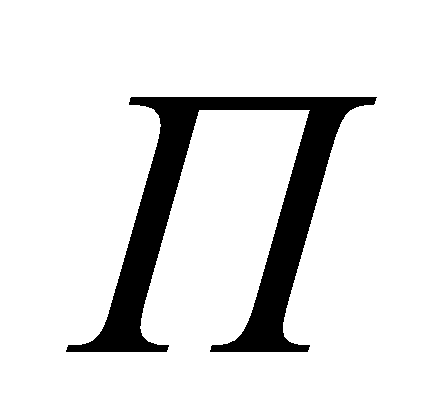 определяет структуру СПМ, а случайный процесс
определяет структуру СПМ, а случайный процесс
 накладывается на структуру
накладывается на структуру
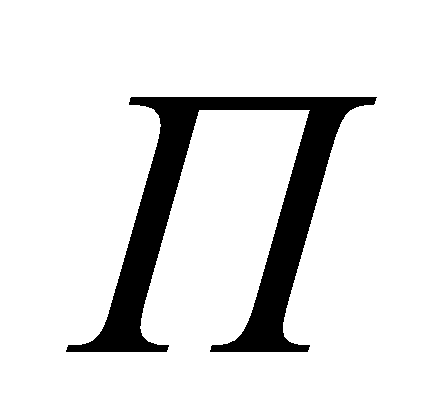 и определяет временные и вероятностные характеристики СПМ.
и определяет временные и вероятностные характеристики СПМ.- Вариационные свойства модели раскрываются через четверку
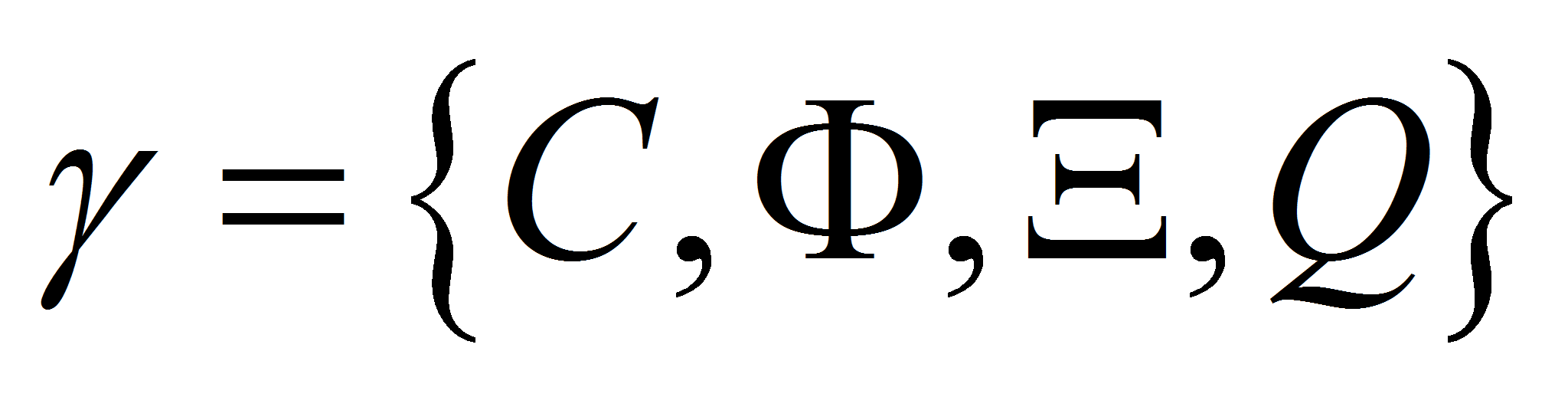 ,
,- где
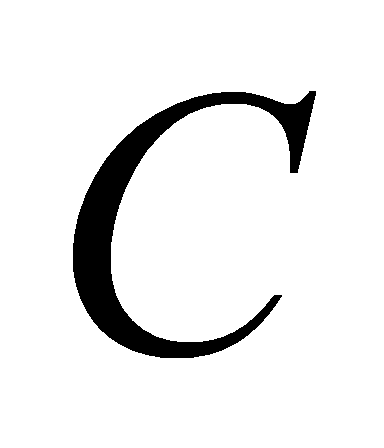 - вектор раскраски позиций;
- вектор раскраски позиций;
 - вектор разметки;
- вектор разметки;
 - вектор занятости;
- вектор занятости;
 - упорядоченное множество очередности заявок.
- упорядоченное множество очередности заявок.- Структура СПМ характеризуется одной из четверок:
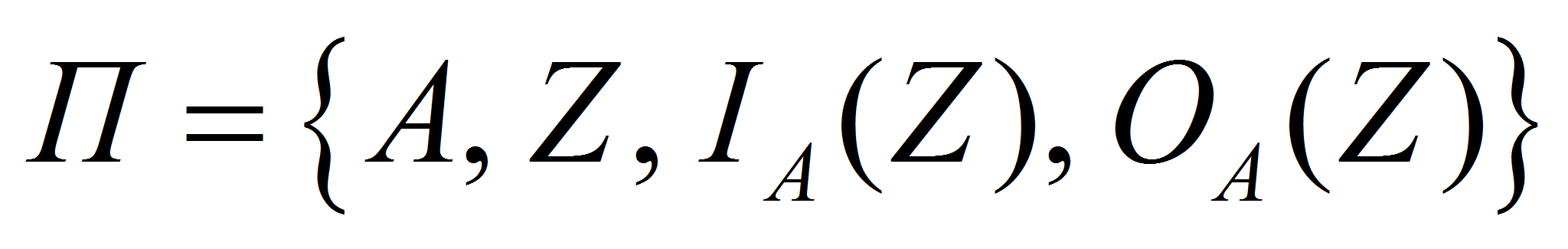 ,
,- или
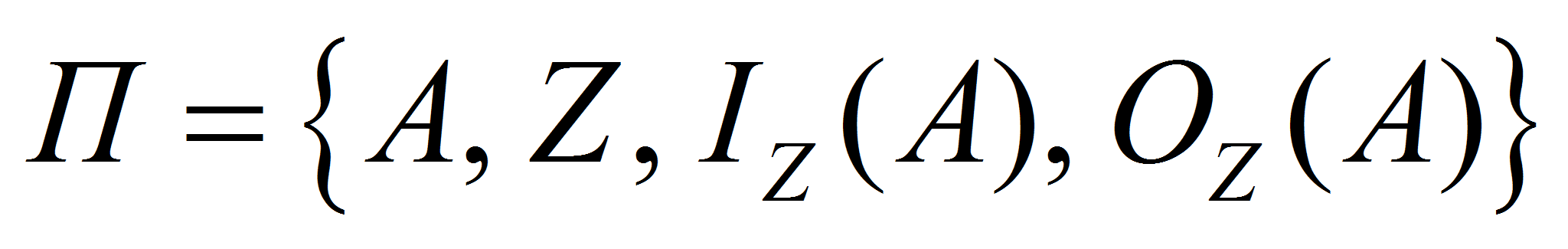 ,
,- где
 - конечное множество позиций;
- конечное множество позиций;
 - конечное множество переходов;
- конечное множество переходов;
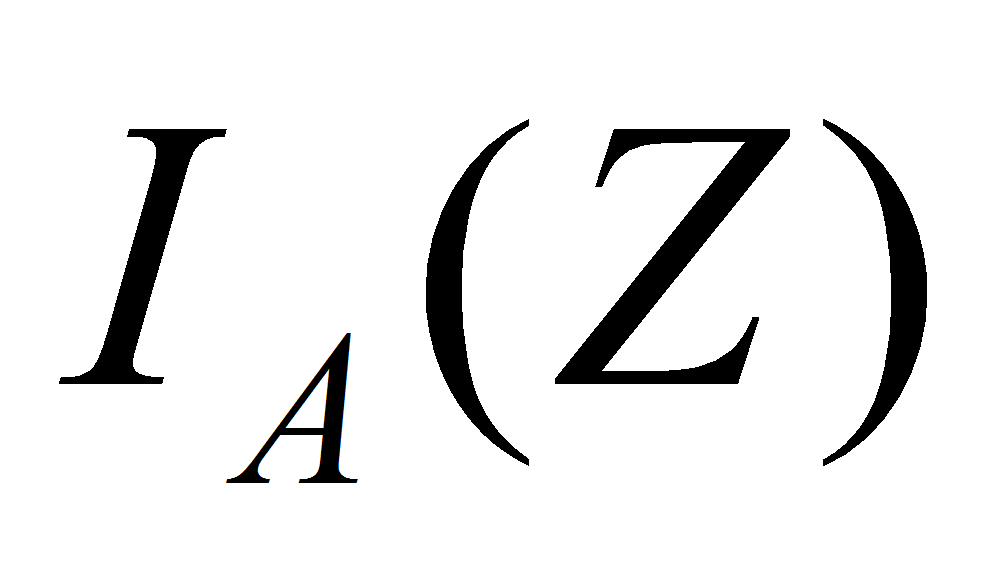 и
и
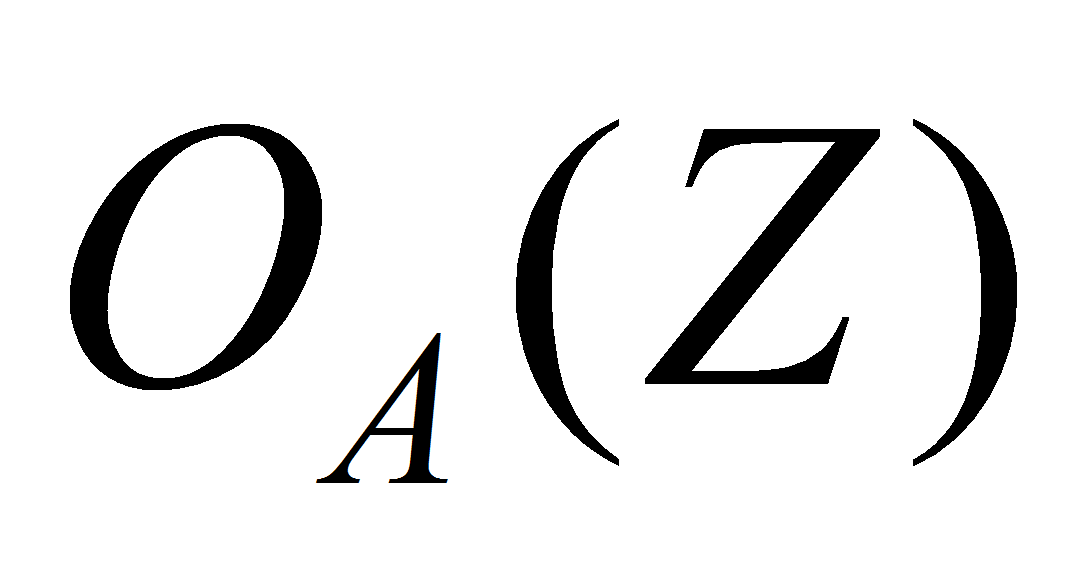 - соответственно входная и выходная функции переходов;
- соответственно входная и выходная функции переходов;
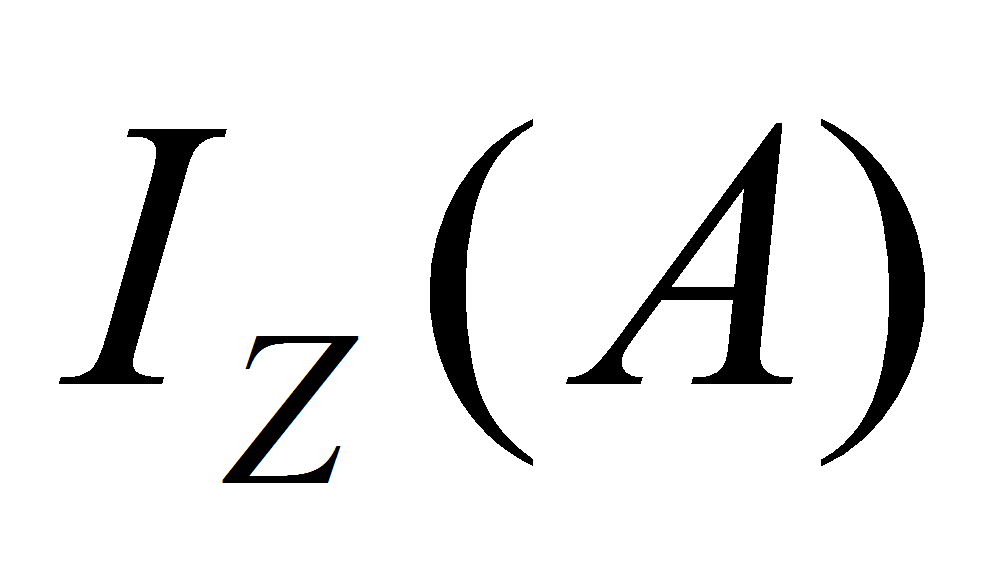 и
и
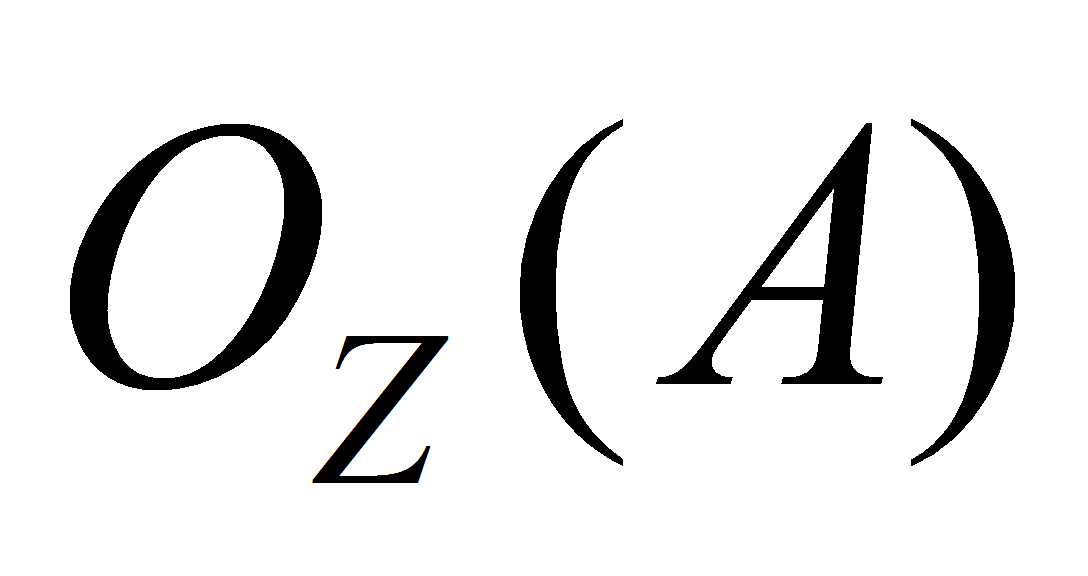 - соответственно входная и выходная функции позиций.
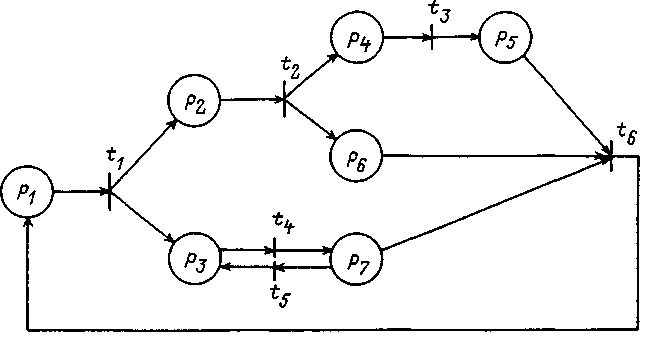
- соответственно входная и выходная функции позиций.- Высоким уровнем наглядности и удобства анализа обладает метод представления СПМ в виде ориентированных взвешенных биграфов, вид которых приведен на рис. 3. В указанных биграфах позиции обозначены кружочками, переходы - жирной чертой, возможность выполнения полушага отмечается стрелкой, над которой указывается плотность распределения времени и вероятность для выполнения полушага из позиции в переход или логические условия для выполнения полушага из перехода в позицию.
- В результате анализа строится непосредственно граф зависимостей, вершинами которого являются выделенные состояния программы. Стоит отметить, что для упрощения построения графа, можно использовать таблицу, строками которой являются переменные, а столбцами – состояния. На пересечении строки и столбца ставиться маркер, если переменная участвует в данном состоянии. Используя сформированную таблицу, можно упростить процесс построения будущего графа. Объясняется это тем, что состояния, не имеющие ни одного маркера, не являются значимыми для построения модели программы, т.к. не могут влиять на ход выполнения операций.
Рис. 3. Пример сети Петри-Маркова
-
- Представленный математический аппарат обладает необходимыми инструментами, позволяющими при моделировании учитывать все перечисленные ранее особенности программного обеспечения реального времени. Использование СПМ помимо ответа на вопрос о достижимости состояний, в которых может возникнуть фатальная для ПО ошибка, даёт возможность прогнозировать моменты перехода системы в эти состояния. Вероятностные и временные характеристики элементов моделей такого типа могут быть рассчитаны по структурно-параметрическим характеристикам исходных алгоритмов и логическим условиям продолжения функционирования процесса, а также по ограничениям на программные реализации алгоритмов.
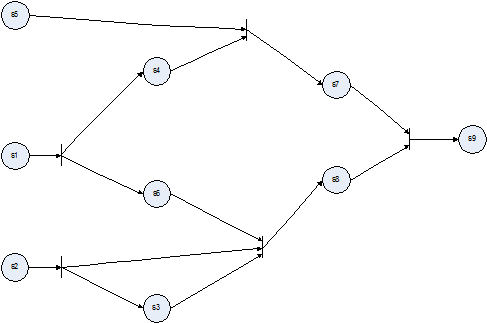
- Для рассматриваемого в данной статье примере программы, с использованием предлагаемой методики выявления информационных зависимостей, построим сеть Петри (Рис. 4). Сеть отражает все информационные зависимости в программе. Также, ее структура позволяет выделить в исходном коде блоки, выполнение которых возможно параллельно.
- В рассматриваемом примере вычисление результатов в блоках s1, s2 может происходить параллельно. Также, отсутствуют зависимости по данным в s4, s6, s3, что говорит о том, что данные операции следует также выполнять обособленно и одновременно. При этом, вычисление s5 может производиться как параллельно с s1, s2, так и s4, s6, s3. Выбор схемы обработки операций и их порядок зависит от того, какие оценки эффективности и оптимальности были выбраны при запуске процесса распараллеливания.
- Представленный математический аппарат обладает необходимыми инструментами, позволяющими при моделировании учитывать все перечисленные ранее особенности программного обеспечения реального времени. Использование СПМ помимо ответа на вопрос о достижимости состояний, в которых может возникнуть фатальная для ПО ошибка, даёт возможность прогнозировать моменты перехода системы в эти состояния. Вероятностные и временные характеристики элементов моделей такого типа могут быть рассчитаны по структурно-параметрическим характеристикам исходных алгоритмов и логическим условиям продолжения функционирования процесса, а также по ограничениям на программные реализации алгоритмов.
Рис. 4. Сеть Петри для рассматриваемого примера
-
- При этом важным требованием остается максимально возможное использование имеющихся ресурсов.
- Заключение
- Рассмотренная методика
построения графа информационных зависимостей предоставляет
исчерпывающую информацию для получения различных схем
распараллеливания вычислений. Использование для моделирования
вычислительного процесса математического аппарата сетей Петри-
Маркова позволить значения оценок времени выполнения
рассматриваемого варианта распараллеливания программы.
- Модель программного обеспечения, построенная сетями Петри, учитывает такие характеристики как случайность времени выполнения операции, логические условия продолжения функционирования системы, параллельное выполнение вычислений, а также соблюдение условия достижимости любого из состояний. Последнее является одним из основных требований, предъявляемых к верифицируемой системе. Таким образом, совместное построение сети Петри и графа информационных зависимостей программы является одним из возможных подходов к решению проблемы распараллеливания вычислений. Граф информационных зависимостей позволяет учитывать все особенности логической и информационной структуры программы, что является основным аспектом при построении моделей программы [4].
- Литература:
- Модель программного обеспечения, построенная сетями Петри, учитывает такие характеристики как случайность времени выполнения операции, логические условия продолжения функционирования системы, параллельное выполнение вычислений, а также соблюдение условия достижимости любого из состояний. Последнее является одним из основных требований, предъявляемых к верифицируемой системе. Таким образом, совместное построение сети Петри и графа информационных зависимостей программы является одним из возможных подходов к решению проблемы распараллеливания вычислений. Граф информационных зависимостей позволяет учитывать все особенности логической и информационной структуры программы, что является основным аспектом при построении моделей программы [4].
- А.Н. Ивутин, Е.И. Дараган Основные подходы к верификации программного обеспечения реального времени // Известия ТулГУ. Серия: Технические науки. Вып. 2. — Тула: Изд. ТулГУ, 2011. — С. 563-567
- А.Н. Ивутин, Е.И. Дараган Применение сетей Петри и метода построения графа информационных зависимостей для решения задач верификации и распараллеливания вычислений // Известия ТулГУ. Серия: Технические науки. Вып. 5, ч. 2. — Тула: Изд. ТулГУ, 2011.
- Е.В. Ларкин, Ю.И. Сабо Сети Петри-Маркова и отказоустойчивость авионики. — Тула: Тул. гос. ун-т., 2004. — 208 с.
- В.С. Карпов, А.Н. Ивутин, Е.И. Дараган Сети Петри-Маркова и верификация программного обеспечения реального времени // Известия ТулГУ. Серия: Технические науки. Номер 4. — Тула: Изд. ТулГУ, 2010. — С. 266-271