Генетический алгоритм планирования конкурирующих за канал передачи данных пластичных заданий

Введение

Существует множество алгоритмов управления очередью заданий и составления расписаний, применимых для задач регулирования загрузки параллельных вычислительных систем [1]. Увеличение эффективности процесса планирования вычислительных заданий повышает утилизацию ресурсов и уменьшает время ожидания результатов расчетов. Увеличение числа критериев планирования способно привести к повышению эффективности алгоритма, но негативно скажется на его сложности. Рассмотрим в качестве одного из критериев пластичность вычислительных заданий [2-4]. Пластичные (moldable) задания обладают способностью производить счет на различном по размеру наборе вычислительных элементов. В данной работе в качестве вычислительного элемента рассмотрим вычислительный узел кластера. Существует определенная нетривиальная зависимость между временем выполнения расчета и количеством используемых вычислительных элементов. В силу сложной внутренней структуры программы тяжело предсказать влияние изменения числа узлов на характеристики расчета задания. В качестве другого критерия рассмотрим влияния конкуренции за канал передачи данных на скорость производимых расчетов [5, 6]. Время расчета любой осуществляющей пересылку данных программы складывается из времени вычислений и времени передачи данных. Соответственно, время обмена данными зависит от статических (пропускная способность, задержки) и динамических (конкуренция за канал) характеристик вычислительной сети.

Большинство существующих реализаций планировщика заданий используют детерминированный алгоритм, согласно которому происходит выбор запускаемых задач и их параметров. Рассмотрим использующий эвристический алгоритм планировщик, производящий поиск наилучшего решения с использованием моделирования хода выполнения заданий. По результатам моделирования планировщик производит оценку плана. В зависимости от полученных значений идет выбор направления дальнейшего поиска решений.

Определим модель задания посредством времени выполнения расчета без учета конкуренции за канал и объемом пересылаемых по сети данных. Последнее позволит произвести моделирование потоков данных и, следовательно, определить динамические характеристики вычислительной сети. Модель требует формализации для конкретных используемых приложений.

В данной работе модель определяется зависимостями объема пересылаемых данных и скоростью счета от заданного числа узлов основанных на статистических данных о работе программы. Оценка плана производится путем моделирования размещения моделей заданий на модели кластера с последующим анализом. Важным вопросом в модели кластера является вычислительная сеть передачи данных. В данном исследовании рассматривается топология "звезда", при этом, время задержки пакетов данных определяются с помощью аналитического решения задачи массового обслуживания с одним обработчиком (маршрутизатором).

Определим способы оценки плана:

• Fr - реальное время завершения. Показывает время, когда закончила расчет последняя задача в очереди.
• Fm – средневзвешенное время завершения последних задач. Мерой веса является объем используемых ресурсов.
• Ja - сумма использованных ресурсов каждой из задач. Уменьшение Ja относительно показателя для статических алгоритмов говорит о том, что для выполнения одного и того же набора задач потребовалось меньше вычислительных ресурсов, т.е. внутренние ресурсы использовались эффективнее.

Алгоритм планирования

Существуют методы решения поставленной задачи, позволяющие найти точное решение. Примером таких методов служит неполной перебор с отбросом неперспективных вариантов. Наиболее известным является метод "ветвей и границ". Данный метод дает глобальный минимум целевой функции, однако размерность решаемых им задач относительно мала. Это обусловлено отсутствием эффективного способа определения нижней границы задачи, поэтому приходится исследовать значительную область решений.

В связи с тем, что точные комбинаторные методы не реализуемы при большой размерности очереди, сделан выбор в пользу приближенных эвристических методов.

Проблема выбора эвристик описана в статье [8]. Генетический алгоритм - это математическая модель эволюции популяции искусственных особей. Генетические алгоритмы (ГА) основаны на механизмах селекции и генетики. Основные принципы генетических алгоритмов изложены Холландом[9].

Задача размещения задач на вычислительных ресурсах сводится к выбору таких параметров запуска, что целевая функция оценки эффективности плана становится минимальна. При планировании происходит размещение всех заданий в очереди. Сначала заполняются доступные ресурсы, а затем идет моделирование дальнейшей загрузки с течением времени. Очевидная глобальная эффективность данного подхода значительно зависит от точности оценки времени выполнения заданий и динамики изменения очереди. Также данный подход требует значительно большего объема ресурсов.

Рассмотрим два варианта соблюдения очереди заданий:

• Строгое соблюдение очереди. При этом не нарушается порядок следования заданий.
• Нестрогое соблюдение очереди[7]. При этом первоочередное задание может откладываться, если это приводит к уменьшению значения целевой функции оценки плана. Строгость соблюдения очереди должна реализовываться через целевую функцию или ограничения на размещения.
• Применим для каждого расписание в ГА кодирование в форме хромосомы[10]. Хромосома 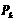состоит из упорядоченного набора генов. Ген в свою очередь состоит из номера задачи и количества узлов на которых будет запущенна задача. Цель состоит в нахождении максимума целевой функции (функции приспособленности). В качестве целевой функции используется оценка Fr (время завершения расчетов). Эволюция популяции моделируется последовательностью поколений 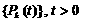. В каждый момент времени t состав популяции меняется. Для каждого последующего поколения отбираются особи с относительно большими значениями функции. Хромосомы подвергаются воздействию генетических операторов, применение которых позволяет получить новое поколение.

Применим следующие генетические операторы:

• Оператор кроссинговера последовательности. Две хромосомы 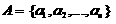и 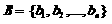выбираются случайным образом из текущей популяции. Случайным образом выбирается точка разреза хромосом (код гена, после которого выполняется выборка произвольной длинны w). Две новые хромосомы и 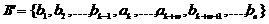получаются путем сохранения хромосом в разрезе и заполнения оставшегося пространства элементами второй хромосомы
• Оператор кроссинговера значения числа узлов. Сохраняет порядок хромосом, но производит обмен значениями числа узлов для генов определенной выборки.
• Мутация перемещения. Осуществляет перестановку произвольного числа задач в очереди, начиная с произвольной позиции.
• Мутация числа узлов. В очереди выбирается произвольная задача для которой производится изменение числа узлов. Новое значение числа узлов образуется путем прибавления случайной, отличной от нуля, величины.

Результаты

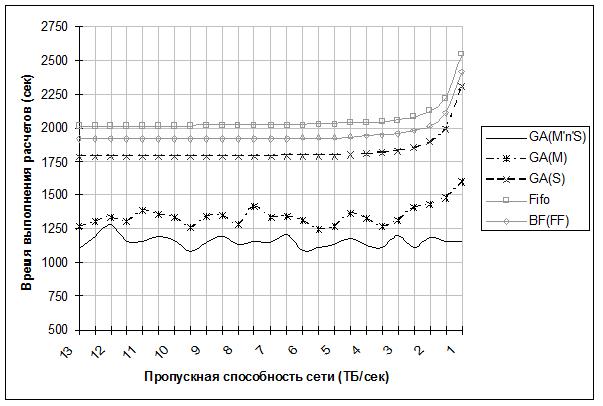
Рис. 1. График зависимости времени выполнения заданий, при снижении пропускной способности сети

В исследовании рассматривалось пять алгоритмов:

• Fifo - первая вставшая в очередь задача, отправляется на расчет первой.
• BF(FF) - первая вставшая в очередь задача, отправляется на расчет. При наличии свободного места, недостаточного для следующий в очереди задачи, на нем запускается первая подходящая в очереди задача.
• GA(M) - генетический алгоритм, применяющий операции только изменения числа узлов для запуска.
• GA(S) - генетический алгоритм, применяющий операции только изменения очередности заданий.
• GA(M'n'S) - генетический алгоритм, применяющий все операции.

На рисунке 1 представлен график зависимости времени выполнения заданий для одного и того же набора задач, при снижении пропускной способности маршрутизатор.

Как видно из графика, наиболее устойчивым к падению производительности сети показал себя алгоритм GA(M'n'S).

Заключение

В результате проведенного моделирования разработанный алгоритм показал свою эффективность в сравнении с выбранными алгоритмами. Полученные результаты показали его особенную эффективность при высокой конкуренции за ресурсы вычислительной сети. Тем не менее, существует множество дополнительных критериев, способных повлиять на качество процесса планирования:

• Учет сложных топологий и гетерогенности.
• Учет возможности остановки выполнения вычислительных заданий различными средствами.
• Учет гибких (mallaeble) заданий, способных изменять число узлов в процессе работы.
• Также необходимо отметить перспективы развития самого алгорима:
• Поиск оптимальных параметров генетического алгоритма.
• Исследования генетических операций приводящих к более качественному решению.

Литература:

1. Michael L Pinedo. "Scheduling: Theory, Algorithms, and Systems" // New York, Springer science 2008.
2. С.Н. Мамойленко, А.В. Ефимов "Алгоритмы планирования решения масштабируемых задач на распределенных вычислительных системах" // Вестник СибГУТИ №2, 2010г. стр. 66-78.
3. L. Barsanti, A. Sodan. "Adaptive job scheduling via predictive job resource allocation" // Lecture notes in computer science, 2007, с.115-140.
4. W. Cirne, F. Berman. "A modal of moldable supercomputer jobs" // 15th International Parallel & Distributed Processing Symp, 2001. URL://www.lsd.dsc.ufpb.br/parars/moldability-model.pdf (дата обращения 23.09.2011).
5. П.Н. Полежаев. "Планирование задач для вычислительного кластера с учетом сети и многопроцессорности узлов" // Параллельные вычисли-тельные технологии (ПАВТ'2011): Труды международной конференции. - Москва, Изд. МГУ, 2011 г. 254-265.
6. А.В. Юлдашев "Минимизация времени выполнения MPI-программ с учетом конкуренции за каналы передачи данных коммуникационной среды кластерной системы" // Вестник УГАТУ №2(42) - Уфа, 2011г, стр 99-105.
7. А.Б. Новиков, С.А. Петунин. "Влияние специализированных алгоритмов планирования заданий на эффективность использования вычислитель-ных ресурсов в частных случаях" // XIII международный семинар "супервычисления и математическое моделирование", РФЯЦ-ВНИИЭФ, 2011г.
8. В.А Чеканин. "Модифицированные эволюционные алгоритмы и программные решения задачи ортоганальной упаковки объектов", диссертация, 2011 г.
9. J.H. Holland. "Adaptation in Natural and Artifitial Systems", University of Michigan, Ann Arbor, 1975 г.
10. Т.С. Шаповалов. "Планирование выполнения заданий в распределенных вычислительных системах с применением генетических алгоритмов", диссертация, 2010 г.