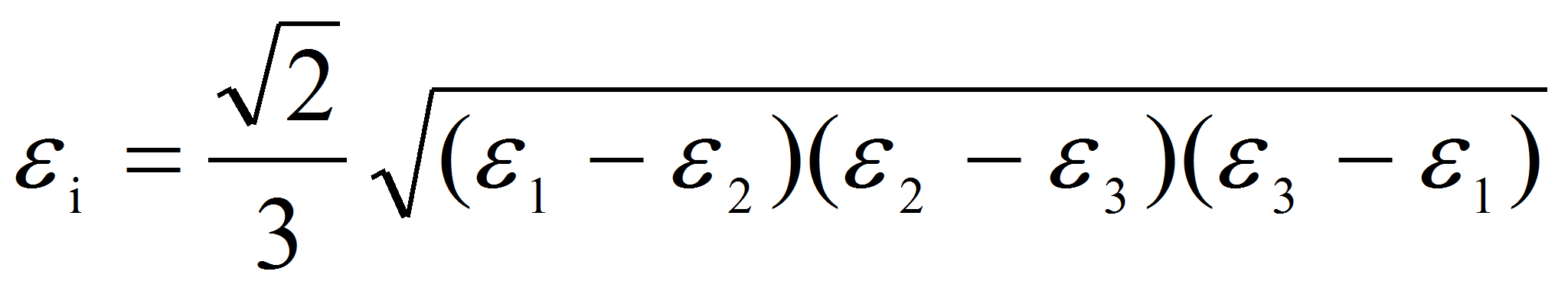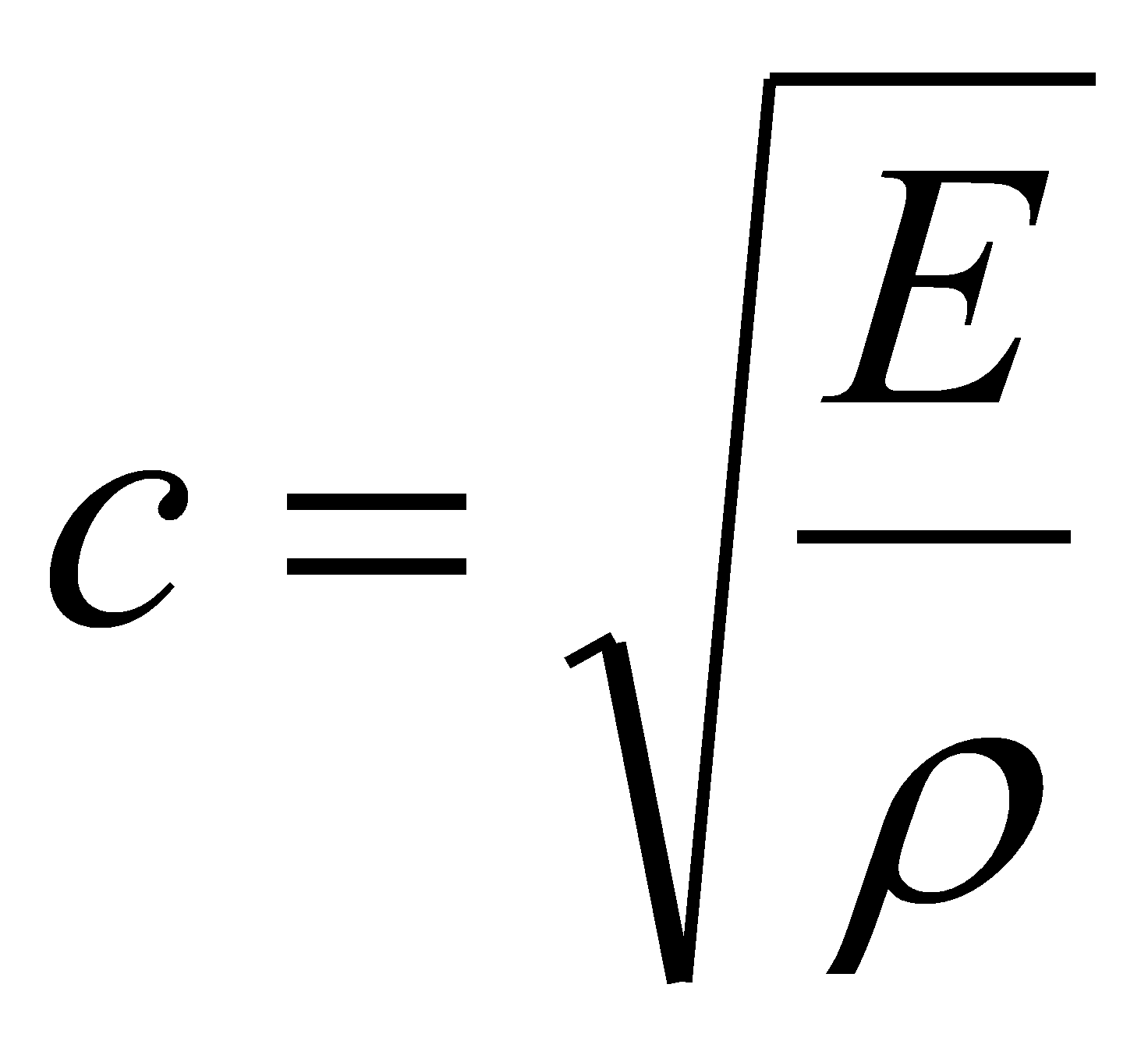Основным методом определения прочности элементов конструкции планера и стоек шасси [2] при соударении с поверхностью являются численные исследования позволяющие с достаточной степенью достоверности решать динамическую задачу соударения конструкции и поверхности. Пример конструкции фюзеляжа беспилотного летательного аппарата показан на рис 1.
Исследования прочности конструкции при ударе проводятся с использованием универсальной конечно-элементной программы ANSYS. Параметры воздействия со стороны поверхности определяются в процессе решения задачи прочности. Существует два метода решения задач взаимодействия: на основе формирования лагранжевой и эйлеровой сетей.
Метод Лагранжа, с элементами постоянной массы, является самым общим методом решения конечно-элементной задачи деформирования конструкции. При использовании лагранжевого метода узловые точки сети исследуемого объекта считаются закрепленными на поверхности и в теле модели объекта. Элементы, на которые разбивается модель, связаны между собой через узловые точки. В процессе заданных взаимодействий объект деформируется, узловые точки перемещаются и элементы искажаются.
Рисунок 1 – Фюзеляж БПЛА
Метод Эйлера с элементами постоянного объема применяется для моделирования движения объектов и различных сред в пространстве. Здесь узловые точки сети фиксированы в пространстве и в разные моменты времени эйлеровы элементы, связанные между собой через узловые точки, наделены различными свойствами. В частности, движение модели объекта через эйлерову сетку моделируется переносом от элемента к элементу массы, количества движения и энергии объекта.
В данном исследовании эйлерова и лагранжева сети использованы водном расчете (рис. 2.2.2) и взаимодействуют между собой через специально задаваемую "соприкасающуюся поверхность". Эта поверхность является непроницаемой границей для среды в эйлеровой сетке. Движущаяся среда воздействует на эту поверхность, вызывая деформацию лагранжевой сети (конструкции).
Первый этап численного моделирования состоит в создании геометрии поверхностей и объемов, участвующих в задаче объектов. Вторым этапом является задание на поверхностях и объемах конечных элементов. В задаче используются два вида элементов - лагранжевые и эйлеровые.
Рисунок 2.2.2 – Построение расчетной сети
Конечно-элементные модели обшивок, стрингеров и нервюр состоят из плоских четырехугольных элементов типа "оболочка".
Для модели используется свойства материала ПС-1 [1], плотностью ρ =0,0001 г/см3 и модулем упругости Е = 0,8 * 103 кгс/см2.
Пространство перед зоной удара заполняется эйлеровыми элементами.
В любом месте этого эйлерого пространства можно задать и "запустить" процесс столкновения. В эйлеровых элементах определяется геометрический объект в виде замкнутого объёма - модель планера. Для нее задаются начальная скорость и свойства.
Модель планера представляет собой сплошное тело в виде прямоугольника, имеющего подкрепляющий силовой набор (рис 2.2.3, 2.2.4).
В качестве общего критерия разрушения для элементов конструкции выбрано достижение действующих эквивалентных деформаций величины допускаемых:
εi,мах ≥ [ε].
Рисунок 3 – Трехмерная твердотельная модель носовой части фюзеляжа
Рисунок 4 – Расчетная сетка носовой части фюзеляжа
При этом действующие эквивалентные деформаций, выраженные через
деформации в главных осях - ε1, ε2, ε3, записываются в виде:
Для принятого представления диаграммы деформирования, действующие напряжения и деформации можно представить в виде сумм упругой и пластической составляющих:
где εy – эквивалентные упругие деформации, εp - эквивалентные накопленные
пластические деформации.
Полагая в момент разрушения для упруго-пластических материалов εi≈εp, ввиду малости упругих деформаций - εy по сравнению с величиной пластических - εp, в качестве допускаемого значения деформации принимается максимальная величина эквивалентных пластических деформаций:
[ε]=( εв-σ02/Е).
Тогда критерий разрушения для элементов конструкции принимает вид
εр,мах ≥ [ε].
Именно этот деформационный критерий разрушения представляется наиболее эффективным. Так как динамический процесс взаимодействия носит колебательный характер, где упругая составляющая деформаций и амплитуда напряжений, возникающих в элементах, быстро меняется, сложно точно зафиксировать момент разрушения по изменению напряжений.
Изменение временного шага в процессе вычислений связано с изменением размера элемента, например, из-за деформаций или разрушения.
Здесь вступает в силу критерий Куранта, который записывается в виде:
где Δ t - минимальный временной шаг, S - параметр меньший единицы, b - минимальный размер элемента, c - скорость звука в среде.
Скорость звука в среде в свою очередь выражается формулой:
где Е - модуль упругости, ρ - плотность среды.
В соответствии с этим критерием, задается начальный и минимальный временные шаги. На каждом шаге расчета вычисляется Δt.
Скорость соударения планера и поверхности, при которой происходит
разрушение, учитывая существенно нелинейные и динамические процессы
взаимодействия, определяется путем проведения серии расчётов с различными скоростями взаимодействия до определения минимальной скорости, при которой выполняется критерий разрушения. При этом величина скорости деформации в рассматриваемых случаях оценивалась с использованием статической диаграммы деформирования материала в билинейной форме.
На основе использования результатов натурных испытаний проведена верификация комплекса ANSYS для решения задачи столкновения конструкции с поверхностью, что позволяет обоснованно с высокой степенью достоверности проводить расчеты.
Особенности расчета:
- Импортирование файла происходит из формата SAT. Для удобства использования свойств материалов масштабируем модель в сантиметры.
- Для расчета используется тип элемента Solid 95.
- Модель разбивается нерегулярной сеткой с шириной элемента 1 см.
- На переднюю кромку прикладывается распределенная q= 100 кгс/м = 1 кгс/см.
По трехмерному расчету видно превышение допустимых нагрузок и разрушение конструкции фюзеляжа. Таким образом, показана методика позволяющая оценить деформации и возможные разрушения фюзеляжа при нерасчетных контактах.
Работа выполнена в рамках ФЦП "Научные и научно-педагогические кадры инновационной России на 2009 – 2013 годы.
- Литература:
- Альшиц И. Я., Благов Б. Н. Проектирование деталей из пластмасс. Справочник. Серия: Б-ка конструктора. М.: Машиностроение. 1977г. 215 с., илл.
Сенюшкин и др. Математическая модель работы шасси при демпфировании динамических воздействий в процессе взлета и посадки летательного аппарата/ Молодой ученый. — 2012. — №4. — С. 41-43.